Главная | Обратная связь | Поможем написать вашу работу!

Поиск по деформируемому многограннику

Впервые метод деформируемого многогранника был предложен Нелдером и Мидом. Они предложили метод поиска, оказавшийся весьма эффективным и легко осуществляемым на ЭВМ. Чтобы можно было оценить стратегию Нелдера и Мида, кратко опишем симплексный поиск Спендли, Хекста и Химсворта, разработанный в связи со статистическим планированием эксперимента. Вспомним, что регулярные многогранники в Eⁿ являются симплексами. Например, как видно из рисунка 1, для случая двух переменных регулярный симплекс представляет собой равносторонний треугольник (три точки); в случае трёх переменных регулярный симплекс представляет собой тетраэдр (четыре точки) и т.д.

Рисунок 1.
Регулярные симплексы для случая двух (а) и трёх (б) независимых переменных.

обозначает наибольшее значение f(x). Стрелка указывает направление
наискорейшего улучшения.

При поиске минимума целевой функции f(x) пробные векторы x могут быть выбраны в точках Eⁿ, находящихся в вершинах симплекса, как было первоначально предложено Спендли, Хекстом и Химсвортом. Из аналитической геометрии известно, что координаты вершин регулярного симплекса определяются следующей матрицей D, в которой столбцы представляют собой вершины, пронумерованные от 1 до (n+1), а строчки – координаты, i принимает значения от 1 до n:

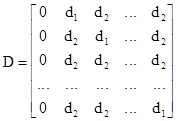– матрица n X (n+1),

где

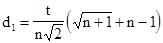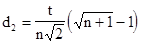t – расстояние между двумя вершинами. Например, для n=2 и t=1 треугольник, приведённый на рисунке 1, имеет следующие координаты:

Вершина	x_1,i	x_2,i
1	0	0
2	0.965	0.259
3	0.259	0.965

Целевая функция может быть вычислена в каждой из вершин симплекса; из вершины, где целевая функция максимальна (точка A на рисунке 1), проводится проектирующая прямая через центр тяжести симплекса. Затем точка A исключается и строится новый симплекс, называемый отражённым, из оставшихся прежних точек и одной новой точки B, расположенной на проектирующей прямой на надлежащем расстоянии от центра тяжести. Продолжение этой процедуры, в которой каждый раз вычёркивается вершина, где целевая функция максимальна, а также использование правил уменьшения размера симплекса и предотвращения циклического движения в окрестности экстремума позволяют осуществить поиск, не использующий производные и в котором величина шага на любом этапе k фиксирована, а направление поиска можно изменять. На рисунке 2 приведены последовательные симплексы, построенные в двумерном пространстве с «хорошей» целевой функцией.

Рисунок 2.
Последовательность регулярных симплексов, полученных при минимизации f(x).
----- проекция

Определённые практические трудности, встречающиеся при использовании регулярных симплексов, а именно отсутствие ускорения поиска и трудности при проведении поиска на искривлённых «оврагах» и «хребтах», привели к необходимости некоторых улучшений методов. Далее будет изложен метод Нелдера и Мида, в котором симплекс может изменять свою форму и таким образом уже не будет оставаться симплексом. Именно поэтому здесь использовано более подходящее название «деформируемый многогранник».

В методе Нелдера и Мида минимизируется функция n независимых переменных с использованием n+1 вершин деформируемого многогранника в Eⁿ. Каждая вершина может быть идентифицирована вектором x. Вершина (точка) в Eⁿ, в которой значение f(x) максимально, проектируется через центр тяжести (центроид) оставшихся вершин. Улучшенные (более низкие) значения целевой функции находятся последовательной заменой точки с максимальным значением f(x) на более «хорошие точки», пока не будет найден минимум f(x).

Более подробно этот алгоритм может быть описан следующим образом.

Пусть , является i-й вершиной (точкой) в Eⁿ на k-м этапе поиска, k=0, 1, …, и пусть значение целевой функции в x^(k)_i равно f(x^(k)_i). Кроме того, отметим те векторы x многогранника, которые дают максимальное и минимальное значения f(x).

Определим

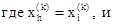
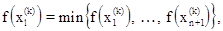
Поскольку многогранник в Eⁿ состоит из (n+1) вершин x₁, …,x_n+1, пусть x_n+2 будет центром тяжести всех вершин, исключая x_h.

Тогда координаты этого центра определяются формулой

(1)

где индекс j обозначает координатное направление.

Начальный многогранник обычно выбирается в виде регулярного симплекса (но это не обязательно) с точкой 1 в качестве начала координат; можно начало координат поместить в центр тяжести. Процедура отыскания вершины в Eⁿ, в которой f(x) имеет лучшее значение, состоит из следующих операций:

1. Отражение – проектирование x^(k)_h через центр тяжести в соответствии с соотношением
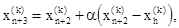(2)
где a>0 является коэффициентом отражения; – центр тяжести, вычисляемый по формуле (1); 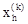– вершина, в которой функция f(x) принимает наибольшее из n+1 значений на k-м этапе.

2. Растяжение. Эта операция заключается в следующем: если , то вектор растягивается в соответствии с соотношением
(3)
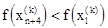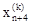где g>1 представляет собой коэффициент растяжения. Если , то заменяется на и процедура продолжается снова с операции 1 при k=k+1. В противном случае заменяется на и также осуществляется переход к операции 1 при k=k+1.

3. Сжатие. Если для всех i¹h, то вектор 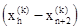сжимается в соответствии с формулой
(4)
где 0<b<1 представляет собой коэффициент сжатия. Затем заменяем на и возвращаемся к операции 1 для продолжения поиска на (k+1)-м шаге.

4. Редукция. Если , все векторы 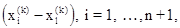уменьшаются в 2 раза с отсчётом от 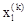в соответствии с формулой
(5)

Затем возвращаемся к операции 1 для продолжения поиска на (k+1)-м шаге.

Критерий окончания поиска, использованный Нелдером и Мидом, состоял в проверке условия

(6)

где e – произвольное малое число, а – значение целевой функции в центре тяжести .

На схеме 1 приведена блок-схема поиска методом деформируемого многогранника, а на рисунке 3 показана последовательность поиска для функции Розенброка, начиная их x⁽⁰⁾=[-1,2 1,0]^T. Деформируемый многогранник в противоположность жёсткому симплексу адаптируется к топографии целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума.

Пуск