Расчет среднеповерхностной температуры нагретой зоны герметичной РЭА.

Содержание.

 

1. Краткие теоретические сведения- стр.2

1.1.Расчёт среднеповерхностной температуры нагретой зоны герметичной РЭА-стр.2

1.2.Расчёт теплового режима кассетной РЭА группы А-стр.5

1.3.Расчёт теплового режима кассетной РЭА группы Б-стр.8

2.Расчёты тепловых режимов -стр.10

2.1.Расчёт среднеповерхностной температуры нагретой зоны герметичной РЭА-стр.10

2.2.Расчёт теплового режима кассетной РЭА группы А-стр.12

2.3.Расчёт теплового режима кассетной РЭА группы Б-стр.14

3.Заключение-стр.19

4.Список источников-стр.20

 

 

Краткие теоретические сведения.

Расчет среднеповерхностной температуры нагретой зоны герметичной РЭА.

Пусть РЭА имеет герметичный корпус в форме прямоугольного параллелепипеда, внутри которого расположено горизонтальное шасси.

Шасси вместе с расположенным на нем деталями представляет собой нагретую зону. Очевидно, анализ нагретых зон в общем случае является громоздким, так как зона содержит детали разных размеров и конфигураций. Для упрощения анализа примем следующие допущения:

1) расстояние между соседними деталями мало ив узких зазорах образуются зоны застойного воздуха;

2) излучение поверхностей радиодеталей и шасси, расположенных “в глубине” нагретой зоны, экранируется соседними деталями и практически не достигает корпуса РЭА;

3) кондуктивные связи “шасси-корпус” слабо влияют на тепловой режим нагретой зоны.

Приведенные допущения подтверждаются опытным путем для современной РЭА, которая характеризуется большой плотностью монтажа.

Представим нагретую зону в виде параллелепипеда, который называется эквивалентной нагретой зоной. Размеры эквивалентной нагретой зоны определяют из факта, установленного опытным путем: объем реальной нагретой зоны и объем эквивалентной зоны должны совпадать. Ширина и длина эквивалентной зоны совпадают с внутренними размерами корпуса. Следовательно,

; ;

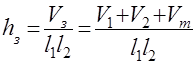
где 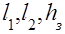- длина, ширина и высота эквивалентной зоны;

- длина и ширина корпуса РЭА;

- толщина стенок корпуса.

Представим

где - внутренняя высота корпуса;

- внутренний объем аппарата.

Величина называется коэффициентом заполнения РЭА.

Зазоры и определяются по очевидным формулам

,

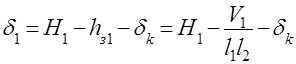где 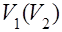- объем деталей над (под) шасси.

По предположению, зазор .

Представим РЭА в виде системы тел, состоящей из оболочки (корпус РЭА), тела (эквивалентная нагретая зона) и среды (воздух, заполняющий свободный объем корпуса). Тепловая схема для изучаемой системы тел приведена на рис. 2,

где

- проводимость “зона-корпус”, обусловленная излучением;

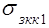- проводимость “зона-корпус”, обусловленная конвекцией над нагретой зоной (область 1);

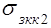- проводимость “зона-корпус”, обусловленная кондукцией под нагретой зоной (область 2);

- проводимость “зона-корпус”, обусловленная конвекцией в области 3.

Проводимость определяется по формуле

,

где 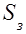- площадь эквивалентной нагретой зоны;

- радиационный коэффициент теплоотдачи.

Аналогичным образом

; ;

где 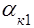- определяется по эмпирической формуле

описывающей конвекцию в ограниченном пространстве при условии, что нагретая сторона расположена снизу.

Поскольку в области 2 движение воздуха отсутствует (нагретая сторона расположена сверху), то

где - теплопроводность воздуха при температуре

В области 3 движение воздуха имеет смешанный характер. Опытным путем установлено, что

Поскольку проводимости , , 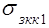, 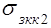зависят от температуры, то уравнение, описывающее тепловую схему (рис. 2), является нелинейным. Рассмотрим определения , основанные на методе последовательных приближений.

2) Расчёт теплового режима кассетной рэа группы A.

Под кассетной РЭА понимают РЭА, в которой навесные элементы, микромодули, интегральные схемы и т.п. располагаются на одинаковых монтажных платах. К группе А относится кассетная РЭА, в которой отсутствует сквозная циркуляция газа между кассетами. Механизмы переноса тепла:

- внутри нагретой зоны - кондукция и излучение через зазоры,
между кассетами;

- от нагретой зоны к корпусу - конвекция и излучение.

К рассматриваемой группе относятся:

- кассетная РЭА, залитая компаундом;

- кассетная РЭА с горизонтальным расположением кассет;

- кассетная РЭА, для которой выполняется одно из следующих
условий: зазоры между кассетами не превышают 2÷3 мм; давление воздуха меньше 10 мм рт.ст.; отсутствует гравитация.

Тепловую модель рассматриваемой кассетной РЭА можно представить в виде герметичного корпуса, внутри которого находится однородная нагретая зона с равномерно распределенными источниками энергии.

Температуру заданного (i -го модуля) кассетной РЭА можно определить по следующей методике:

1. Методом тепловых характеристик или методом последовательных приближений определяют температуру корпуса t_K,

2. Методом последовательных приближений определяют температуру нагретой зоны t_з,

3. Заменяют нагретую зону однородным анизотропным телом с тепловыми проводимостями λ_x, λ_y, λ_z.

4. Рассматривая нагретую зону как твердое тело, внутри которого равномерно распределены источники тепловой энергии и на границе которого поддерживается температура t_з, решают дифференциальное уравнение теплопроводности и определит температурное поле t = f (x, y, z), т.е. температуру любого модуля РЭА.

Поскольку п.1-2 являются стандартными для любой герметичной РЭА, в настоящем разделе они не рассматриваются.

Рассмотрим способ определения проводимостей анизотропного тела. Обозначим L_x, L_y, L_z - размеры нагретой зоны вдоль координатных осей.

Выделим в нагретой - зоне элементарною ячейку. Обозначим область печатной платы,область модуля,область воздушной прослойки, перпендикулярной оси X (оси Y и оси Z соответственно),область воздушной прослойки над модулем;

l_x, l_y, l_z - размеры элементарной ячейки вдоль соответствующих координатных осей;

l_ix, l_iy, l_iz - размеры i -ой области вдоль соответствующих координатных осей.

Размеры l_x, l_y, l_z,l_ix, l_iy и l_iz определяются усреднением размеров всех модулей нагретой зоны.

Очевидно теплофизические параметры областей отличаются, т.е. элементарная ячейка неоднородна. Заменим неоднородную ячейку однородным параллелепипедом l_x x l_y x l_z.

Такая замена правомерна, если тепловые проводимости σ_x, σ_y, σ_z параллелепипеда равны соответствующим проводимостям элементарной ячейки. Проводимости σ_x, σ_y, σ_z определяются по тепловым схемам элементарной ячейки,где σ_x, σ_y, σ_z, σ_ix, σ_iy, σ_iz -проводимости i -ой области ячейки вдоль соответствующей координатной оси. В общем случае

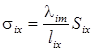
где λ_ix - коэффициент теплопроводности i -ой области вдоль оси X;

l_i - размер i -ой области вдоль оси X;

Аналогичным образом определяются проводимости σ_iy, σ_iz. Тепловые проводимости параллелепипеда равны

;

Следовательно, коэффициенты теплопроводности анизотропного тела

; ;

Поскольку температура зоны известна (см.п.2), в установившемся режиме нагретую зону можно рассматривать как твердое тело, на поверхности которого поддерживается температура t_з, т.е. граничные условия 1-го рода. Дифференциальное уравнение теплопроводности имеет вид:

где W - объемная плотность источников энергии, определяемая как

,[Вт/м³]

где Р - суммарная мощность источников тепловой энергии.

Решение уравнения теплопроводности имеет вид:

- температура в центре нагретой зоны

[°C]

С - параметр, зависящий от λ_x, λ_y, λ_z и размеров зоны; - температура i -го модуля

[°C]

L_i - расстояние от центра зоны до ее поверхности по прямой, проходящей через модуль i;

l_i - - расстояние от центра зоны до i- го модуля.

Поделиться:

Воспользуйтесь поиском по сайту: