 |
Метод проекций. Способы проецирования
|
|
|
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3
ТЕМА: ШРИФТЫ И НАНЕСЕНИЕ РАЗМЕРОВ
ПЛАН
1.Основы начертательной геометрии
2.Метод проекций. Способы проецирования
3.Ортогональное проецирование
ОСНОВЫ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Начертательная геометрия является одной из фундаментальных наук, составляющих основу инженерно-технического образования. Она изучает методы изображений пространственных геометрических фигур на плоскости и способы решения по этим изображениям метрических и позиционных задач в пространстве.
Начертательная геометрия используется также при конструировании сложных поверхностей технических форм в авиационной, судостроительной и других отраслях транспорта и промышленности.
Методы начертательной геометрии позволяют решать многие прикладные задачи специальных инженерных дисциплин (механики, химии, кристаллографии, картографии, инструментоведения и др.)
При проектировании и изображении различных транспортных конструкций и сооружений также широко используются методы начертательной геометрии.
Конструирование сложных форм поверхностей, автоматизированное проектирование и компьютерная графика находят все большее применение при создании современной транспортной техники.
Начертательная геометрия развивает у человека пространственное мышление, без которого немыслимо никакое инженерное творчество.
Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записи геометрических предложений и решения задач в начертательной геометрии предлагается пользовать геометрический язык, составленный из следующих обозначений и символов.
|
|
|
Геометрическая фигура обозначается − Ф.
Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:
A, B, C, D, …,L, M, N, …
1, 2, 3, 4, …, 12, 13, 14, …
Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
a, b, c, d, …,l, m, n, …
Линии уровня обозначаются: h − горизонталь; f − фронталь; p − профильная прямая;
Для прямых используются также следующие обозначения:
(AB) − прямая, проходящая через точки A и B;
[AB) − луч с началом в точке А;
[AB] − отрезок прямой, ограниченный точками A и B.
Поверхности обозначаются строчными буквами греческого алфавита:
α, β, γ, δ, …, ζ, η, λ, …
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α (a b) − плоскость α определяется параллельными прямыми a и b;
β (d1d2g α) − поверхность β определяется направляющими d1 и d2, образующей g и плоскостью параллелизма α.
Углы обозначаются:
АВС − угол с вершиной в точке В, а также αº, βº, …, φº,..,
Угловая величина (градусная мера) обозначается знаком, который ставится над углом:
φº − величина угла φ.
Прямой угол отмечается квадратом с точкой внутри.
Для плоскостей проекций приняты обозначения:
π1 π2 π3, где π1 − горизонтальная плоскость проекций;
π2 − фронтальная плоскость проекций;
π3 − профильная плоскость проекций;
При замене плоскостей проекций или введении новых плоскостей проекций последние обозначаются π4, π5 и т.д.
Оси проекций обозначаются: x,y,z, где x − ось абсцисс; y− ось ординат; z − ось аппликат. Постоянную прямую эпюра Монжа обозначают k.
Проекции точек, линий поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением нижнего индекса, соответствующего плоскости проекций, на которой они получены:
|
|
|
A1, B1, C1, D1, …,L1, M1, N1, … − горизонтальные проекции точек;
A2, B2, C2, D2, …,L2, M2, N2, … − фронтальные проекции точек;
A3, B3, C3, D3, …,L3, M3, N3, …− профильные проекции точек;
а1, b1, c1, d1, …,l1, m1, n1, … − горизонтальные проекции линий;
a2, b2, c2, d2, …,l2, m2, n2, … − фронтальные проекции линий;
a3, b3, c3, d3, …,l3, m3, n3, … − профильные проекции линий;
α1, β1, γ1, δ1, …, ζ1, η1, λ1, …− горизонтальные проекции поверхностей;
α2, β2, γ2, δ2, …, ζ2, η2, λ2, …− фронтальные проекции поверхностей;
α3, β3, γ3, δ3, …, ζ3, η3, λ3, …− профильные проекции поверхностей.
Следы прямых (линий) обозначаются прописными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекций, которую пересекает линия.
Например: H − горизонтальный след прямой (линии) а;
F − фронтальный след прямой (линии) а;
P − профильный след прямой (линии) а.
Следы плоскостей (поверхностей) обозначаются теми же буквами, что горизонталь и фронталь, с добавлением верхнего индекса, подчеркивающего, что эти линии лежат в плоскости проекций и принадлежат плоскости (поверхности).
Например: h0 − горизонтальный след плоскости (поверхности);
f0 − фронтальный след плоскости (поверхности);
p0 − профильный след плоскости (поверхности).
Основные операции:
− параллельность элементов;
≡ − совпадение двух геометрических элементов;
− перпендикулярность элементов;
^ − знак, соответствующий союзу «и»;
= − результат геометрической операции;
∩ − пересечение двух элементов;
− знак принадлежности и включения для точки;
− знак объединения;
− принадлежность одного геометрического элемента другому;
− скрещивающиеся прямые.
МЕТОД ПРОЕКЦИЙ. СПОСОБЫ ПРОЕЦИРОВАНИЯ
Проекцией точки А на плоскость проекций π1 называется точка А1 пересечения проецирующей прямой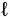 
с плоскостью проекций π 1, проходящей через точку А, (рис. 1):
Проекция любой геометрической фигуры есть множество проекций всех ее точек. Направление проецирующих прямых 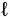и положение плоскостей π1 определяют аппарат проецирования.
Центральным проецированием называется такое проецирование, при котором все проецирующие лучи исходят из одной точки S – центра проецирования (рис. 2).
|
|
|
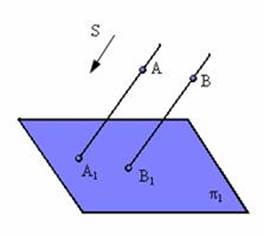
Параллельным проецированием называют такое проецирование, при котором все проецирующие прямые параллельны заданному направлению S (рис. 3).
.
Рисунок 1 – Проекция точки А на плоскость проекций π1
.
Рисунок 2 – Пример центрального проецирования
.
Рисунок 3 – Пример параллельного проецирования
Параллельное проецирование представляет собой частный случай центрального проецирования, когда точка S находится на бесконечно большом расстоянии от плоскости проекций π1.
При заданном аппарате проецирования каждой точке пространства соответствует одна и только одна точка на плоскости проекций.
Одна проекция точки не определяет положения этой точки в пространстве. Действительно, проекции А1 может соответствовать бесчисленное множество точек А’, А’’, …, расположенных на проецирующей прямой 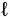(рис. 4).
Для определения положения точки в пространстве при любом аппарате проецирования необходимо иметь две ее проекции, полученных при двух различных направлениях проецирования (или при двух различных центрах проецирования).
.
Рисунок 4 – Пример расположения множества точек на проецирующей прямой
Так, из рис. 5 видно, что две проекции точки А (А1 и А2), полученные при двух направлениях проецирования S1 и S2, определяют единственным образом положение самой точки А в пространстве – как пересечение проецирующих прямых 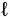1 и 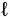2, проведенных из проекций А1 и А2 параллельно направлениям проецирования S1 и S2.
Рисунок 5 – Определение положения точки А в пространстве
|
|
|
12 |
