 |
Исследование биквадратных уравнений
|
|
|
|
Возьмем биквадратное уравнение
ax4 + bx2 + c = 0,
где a, b, c –действительные числа, причем а > 0. Введя вспомогательную неизвестную y = x², исследуем корни данного уравнения, и результаты занесем в таблицу (см. приложение №1)
Формула Кардано
Если воспользоваться современной символикой, то вывод формулы Кардано может иметь такой вид:
х = 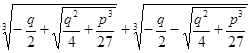
Эта формула определяет корни общего уравнения третей степени:
ax3 + 3bx2 + 3cx + d = 0.
Эта формула очень громоздкая и сложная (она содержит несколько сложныных радикалов). Она не всегда примениться, т.к. очень сложна для заполнения.
Симметричные уравнения третей степени
Симметричными уравнениями третей степени называют уравнения вида
ax³ + bx² +bx + a = 0 (1)
или
ax³ + bx² - bx – a = 0 (2)
где a и b – заданные числа, причём a ¹ 0.
Покажем, как решаются уравнение (1).
Имеем:
ax³ + bx² + bx + a = a(x³ + 1) + bx(x + 1) = a(x + 1) (x² - x + 1) + bx(x + 1) = (x + 1) (ax² +(b – a)x + a).
Получаем, что уравнение (1) равносильно уравнению
(x + 1) (ax² +(b – a)x + a) = 0.
Значит его корнями, будут корни уравнения
ax² +(b – a)x + a = 0
и число x = -1
аналогично решается уравнение (2)
ax³ + bx² - bx - a = a(x³ - 1) + bx(x - 1) = a(x - 1) (x² + x + 1) + bx(x - 1) = (x - 1) (ax2 + ax + a + bx) = (x - 1) (ax² +(b + a)x + a).
1) Пример:
2x³ + 3x² - 3x – 2 = 0
Ясно, что x1 = 1, а
х2 и х3 корни уравнения 2x² + 5x + 2 = 0,
Найдем их через дискриминант:
x1,2 = 
x2 = - 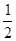 , x3 = -2
, x3 = -2
2) Пример:
5х³ + 21х² + 21х + 5 = 0
Ясно, что x1 = -1, а
х2 и х3 корни уравнения 5x² + 26x + 5 = 0,
Найдем их через дискриминант:
x1,2 = 
x2 = -5, x3 = -0,2.
Возвратные уравнения
Возвратное уравнение – алгебраическое уравнение
а0хn + a1xn – 1 + … + an – 1x + an =0,
|
|
|
в котором ак = an – k, где k = 0, 1, 2 …n, причем, а ≠ 0.
Задачу нахождения корней возвратного уравнения сводят к задаче нахождения решений алгебраического уравнения меньшей степени. Термин возвратные уравнения был введён Л. Эйлером.
Уравнение четвёртой степени вида:
ax4 + bx3 + cx2 + bmx + am² = 0, (a ≠ 0).
Приведя это уравнение к виду
a (x² + m²/x²) + b(x + m/x) + c = 0, и y = x + m/x и y² - 2m = x² + m²/x²,
откуда уравнение приводится к квадратному
ay² + by + (c-2am) = 0.
Пример:
3х4 + 5х3 – 14х2 – 10х + 12 = 0
Разделив его на х2, получим эквивалентное уравнение
3х2 + 5х – 14 – 5 ×  , или
, или
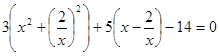
Где 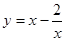 и
и 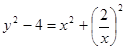
3(y2 - 4) + 5y – 14 = 0, откуда
y1 = 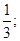 y2 = -2, следовательно
y2 = -2, следовательно
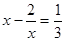 и
и  , откуда
, откуда
х1,2 = 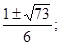
х3,4 = 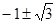
Ответ: х1,2 = 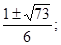 х3,4 =
х3,4 = 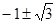 .
.
Частным случаем возвратных уравнений являются симметричные уравнения. О симметричных уравнениях третей степени мы говорили ранее, но существуют симметричные уравнения четвертой степени.
Симметричные уравнения четвертой степени.
1) Если m = 1, то это симметричное уравнение первого рода, имеющее вид
ax4 + bx3 + cx2 + bx + a = 0 и решающееся новой подстановкой
y = 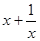
2) Если m = -1, то это симметричное уравнение второго рода, имеющее вид
ax4 + bx3 + cx2 - bx + a = 0 и решающееся новой подстановкой
y = 
Схема Горнера
Для деления многочленов применяется правило “деления углом”, или схема Горнера. С этой целью располагают многочлены по убывающим степеням х и находят старший член частного Q(x) из условия, что при умножении его на старший член делителя D(x) получается старший член делимого P(x). Найденный член частного умножают, затем на делитель и вычитают из делимого. Старший член частного определяют из условия, что он при умножении на старший член делителя даёт старший член многочлена разности и т.д. Процесс продолжается до тех пор, пока степень разности не окажется меньше степени делителя.(см. приложение №2).
|
|
|
В случае уравнений R = 0 этот алгоритм заменяется схемой Горнера.
Пример:
х3 + 4х2 + х – 6 = 0
Находим делители свободного члена ±1; ± 2; ± 3; ± 6.
Левую часть уравнения обозначим f(x). Очевидно, что f(1) = 0, x1 = 1. Делим f(x) на х – 1. (см. приложение №3)
Значит,
х3 + 4х2 + х – 6 = (х – 1) (х2 + 5х + 6)
Последний множитель обозначим через Q(x). Решаем уравнение Q(x) = 0.
х2,3 = 
Ответ: 1; -2; -3.
В этой главе мы привели некоторые формулы решения различных уравнений. Большинство этих формул решения уравнений частного характера. Эти свойства очень удобны так, как гораздо легче решать уравнения по отдельной формуле для этого уравнения, а не по общему принципу. К каждому из способов мы привели доказательство и несколько примеров.
Заключение
В первой главе была рассмотрена история возникновения квадратных уравнений и уравнений высших порядков. Различные уравнения решали более 25 веков назад. Множество способов решения таких уравнений были созданы в Вавилоне, Индии. Потребность в уравнениях была и будет.
Во второй главе приведены различные способы решения (нахождения корней) квадратных уравнений и уравнений высших порядков. В основном это способы решения для уравнений частного характера, то есть к каждой группе уравнений, объединенных какими- либо общими свойствами или видом, приведено особое правило, которое применяется только для этой группы уравнений. Этот способ (подбора к каждому уравнению собственной формулы) гораздо легче, чем нахождение корней через дискриминант.
В этом реферате достигнуты все цели и выполнены основные задачи, доказаны и разучены новые, ранее неизвестные формулы. Мы проработали много вариантов примеров перед тем, как занести их в реферат, по этому мы уже представляем, как решать некоторые уравнения. Каждое решение пригодится нам в дальнейшей учебе. Этот реферат помог классифицировать старые знания и познать новые.
Список литературы
1. Виленкин Н.Я. “Алгебра для 8 класса”, М., 1995.
2. Галицкий М.Л. “Сборник задач по алгебре”, М. 2002.
3. Даан-Дальмедико Д. “Пути и лабиринты”, М., 1986.
4. Звавич Л.И. “Алгебра 8 класс”, М., 2002.
5. Кушнир И.А. “Уравнения”, Киев 1996.
6. Савин Ю.П. “Энциклопедический словарь юного математика”, М., 1985.
|
|
|
7. Мордкович А.Г. “Алгебра 8 класс”, М., 2003.
8. Худобин А.И. “Сборник задач по алгебре”, М., 1973.
9. Шарыгин И.Ф. “Факультативный курс по алгебре”, М., 1989.
Приложение 1
Исследование биквадратных уравнений
| C | b |
Выводы | ||
| О корнях вспомогательного уравнения ay² +by+c=0 | О корнях данного уравнения a(x²)² +bx² +c=0 | |||
| C < 0 | b- любое действительное число | y < 0; y > 0 1 2 | x = ±Öy 1,2 2 | |
| C > 0 | b<0 | D > 0 | y > 0 1,2 | x = ±Öy 1,2,3,4 1,2 |
| D = 0 | y > 0 | x = ±Öy 1,2. | ||
| D < 0 | Нет корней | Нет корней | ||
| b ≥ 0 | y < 0 1,2 | Нет корней | ||
| Нет корней | Нет корней | |||
| y > 0; y < 0 1 2 | x = ±Öy 1,2 1 | |||
| C = 0 | b > 0 | y = 0 | x = 0 | |
| b = 0 | y = 0 | x = 0 | ||
| b < 0 | y = 0 | x = 0 | ||
Приложение 2
Деление многочлена на многочлен «уголком»
| A0 | a1 | a2 | ... | an | c | |
| + | ||||||
| b0c | b1c | … | bn-1c | |||
| B0 | b1 | b2 | … | bn | = R (остаток) | |
Приложение 3
Схема Горнера
| Корень | |||||
| 1 | 4 | 1 | -6 | 1 |
| х1 = 1 | |||||
| сносим | 5 | 6 | 0 | ||
 
|  1 1
|  1×1 +4 = 5 1×1 +4 = 5
| 5×1 + 1 = 6 | 6×1 – 6 = 0 | |
| корень | |||||
| х1 = 1 |
|
|
|


