 |
Различные методы для расчета надежности системы с учетом восстановления и без учета восстановления.
|
|
|
|
Основы теории надежности.
Общие сведения о технической диагностике и надежности.
Диагноз распознавания: Объект, состояние которого определено, называется объектом диагноза.
Диагностика представляет собой процесс исследования объекта диагноза. Завершением этого исследования является получение результата диагноза, т.е. заключение о состоянии объекта (объект исправен, объект не исправен, в объекте имеется такая то неисправность). Диагностика – отрасль знаний, включающая в себя теорию и методы организации процессов диагноза, а так же принципы построения средств диагноза. Когда объектом диагноза является объекты технической природы, говорят о технической диагностике. Техническая диагностика решает три типа задач по определению состояний технических объектов:
1) Задачи по определению состояния, в котором находится объект в настоящий момент времени. Это задачи диагностики;
2) Задачи по предсказанию состояния, в котором окажется объект, в некотором роде это будет момент времени. Это задача прогноза прогнозирования. К задачам технического прогнозирования относятся задачи по назначению периодичности профилактики и ремонта;
3) Задачи определения состояния, в котором находился объект в некоторый момент времени в прошлом. Это задачи генеза отрасль, решающая задачи этого типа называется технической генетикой. К этим задачам относятся, например, причины аварии.
В жизни любого объекта, как некоторого изделия всегда можно выделить два этапа: производство и эксплуатация данного объекта. Бывает так же этап хранения этого объекта.
Для любого объекта на каждом этапе его жизни задаются определенные технические требования. Желательно, чтобы объект всегда соответствовал этим требованиям. Однако в объекте могут возникнуть неисправности, нарушающие указанное соответствие прибора. Тогда задача состоит в том, чтобы создать на этапе производства или восстановить нарушенную неисправность (которая может появиться на этапах эксплуатации или хранения) в соответствии с заданными техническими требованиями прилагаемыми объекту.
|
|
|
Решение этой задачи невозможно без эпизодического или непрерывного диагноза состояния объекта. Состояние объекта определяется его надежностью. Надежность: это свойство объекта выполняемых заданных функций сохранения, во время значений и установленных эксплуатационных показателей в заданных режимах и условиях использования, технического обслуживания, ремонта и т.д.
Исправное состояние: это состояние, при котором прибор соответствует всем требованиям устнормативной – технической документации.
Неисправное состояние: это состояние, при котором прибор, объект не соответствует хотя бы одному из требований нормативно – технической документации.
Работоспособное состояние: это состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения заданных нормативов в пределах установленных документацией.
Неработоспособное состояние: это состояние, при котором значения хотя бы одного заданного параметра не соответствуют нормативно – технической документации.
Понятие повреждение заключается в нарушении исправного состояния изделия при сохранении его работоспособности. Для любого изделия существуют понятия: дефект, неисправность, отказ, сбой и ошибка.
Дефект: это отклонение от параметров изделия относительно заданных в нормативно – технической документации.
Неисправность: форматированное представление факта проявления дефекта на входах и выходах изделия.
|
|
|
Отказ: дефекты, связанные с необратимыми нарушениями характеристик изделия, приводящим к нарушению его работоспособного состояния.
Сбой: дефект, заключающийся в том, что в результате временного изменения параметров изделия в течение некоторого периода времени оно будет функционировать непрерывно. Причем его работоспособность восстанавливается самонаправленно. Помехи, воздействующие на работоспособность.
Ошибки: (для дискретной техники) называют неправильное значение сигналов на внешних входах изделия, вызванное неисправностями, переходными процессами или помехами, воздействующими на изделие.
Число дефектов, неисправностей, отказов, сбоев, одновременно присутствующих в изделии называют кратностью.
Кратность ошибок определена не только кратностью неисправности, из-за которой она возникла, но и структурной схемой изделия, т.к. в результате имеющихся разветвлений в схеме однократная неисправность может вызвать многократную ошибку в последовательных цепях.
Безотказность: свойство изделия, в котором он непрерывно сохраняет работоспособность в течение некоторого времени.
Ремонтопригодность: свойство изделия, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения его отказов, повреждений и устранения их путем ремонта и технического обслуживания.
Показатели безотказности:
1) Вероятность безотказной работы P(t) – это вероятность того, что в заданном интервале времени t в изделии не возникает отказа.
0£ P(t) £1; P(o) = 1; P(¥) = 0;
Функция P(t) является монотонно убывающей функцией, т.е. в процессе эксплуатации и хранения надежность только убывает. Для определения P(t) используется следующая статическая оценка:

где N – число изделий, поставленных на испытание (эксплуатацию).
N0 – число изделий, отказавших в течении времени t.
2) Вероятность бессбойной работы Рсб(t) – это вероятность того, что в заданном интервале времени t будет отсутствовать сбой в изделии.
Рсб(t) = 1- Q сб(t); где - Q сб(t) функция распределения сбоев в течение времени t.
Для определения стабильности оценки мы имеем формулу:
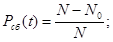
где N – число изделий поступивших на эксплуатацию.
N0 – число изделий, в которых произошел сбой в течение времени t.
|
|
|
3) Интенсивность отказа l(t) – это условная плотность вероятности возникновения отказа не восстанавливаемого объекта, определенного рассмотренного момента времени, при условии, что до этого момента отказ не возник.
Для определенно l(t) используется следующая статистическая оценка:
 где n(Dt) – число отказавших изделий в интервал времени (Dt).
где n(Dt) – число отказавших изделий в интервал времени (Dt).
Nср(Dt) – ссреднее число исправных изделий в интервал времени (Dt).
 ;
;
4) Средняя наработка до отказа (среднее время безотказной работы) Т – это математическое ожидание наработки до первого отказа определяется так:

Эти показатели рассчитаны на изделие, которое не подлежит восстановлению.
Показатели ремонтопригодности:
1) Вероятность восстановления s(t) – это вероятность того, что отказавшее изделие будет восстановлено в течение времени t.
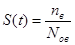 ;
;
где nв – число изделий время восстановления которых было < (меньше) заданного времени t. Nов – число изделий оставшихся на восстановлении.
2) Интенсивность восстановленного М(t) – условная плотность распространения времени восстановления для момента времени t при условии, что до этого момента восстановление изделия не произошло.
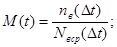 где nв(Dt) – число восстановленных изделий за время Dt. Nв.ср(Dt) – среднее число изделий которые, не были восстановлены в течение времени Dt.
где nв(Dt) – число восстановленных изделий за время Dt. Nв.ср(Dt) – среднее число изделий которые, не были восстановлены в течение времени Dt.
3) Среднее время восстановления Тв – это натуральная величина ожидания восстановления. 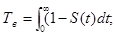
|
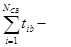
Статистическая оценка:
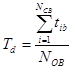 ;
;
4) Коэффициент готовности Кг (t) – это вероятность того, что изделие работоспособно в произвольный момент времени t.
Стационарный режим: t ® ¥.
|
Стационарная оценка: 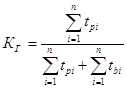 ;
;
где tpi i – ый интервал времени исправной работы изделия.
tbi – интервал времени восстановления изделия.
n – число отказов изделия.
 Коэффициент оперативной готовности Копер. (t, t) – работоспособна в произвольный момент времени t.
Коэффициент оперативной готовности Копер. (t, t) – работоспособна в произвольный момент времени t.
5)  Коэффициент оперативной готовности Копер. (t, t) – это вероятность того, что аппаратура будет работоспособна в произвольный момент времени t. и безотказно проработает заданное время r.
Коэффициент оперативной готовности Копер. (t, t) – это вероятность того, что аппаратура будет работоспособна в произвольный момент времени t. и безотказно проработает заданное время r.
|
|
|
Копер.(t, t) = Кг(t) · Р(t)
Для определения Копер. имеется статистическая оценка:

Законы распределения случайных величин, используемые в теории надежности.
Время m/q между соседними отказами для элементов аппарата является непрерывной случайной, величиной, которая характеризует некоторый закон распределения. Наиболее часто используется следующий закон распределения:
Экспонентой распределения Вейбула - называется нормальное распределение Y и другие распределения. Экспоненциальное OCH – показатель надежности при нем могут быть оценены исходя из следующей зависимости
Экспоненциальные показатели - основные показатели надежности при не при них могут оценены исходя из следующей зависимости: P(t) = e-lt; Q(t) = 1 - e-lt; или
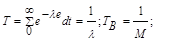
l - это параметр экспоненциального распределения.
lt << 1, то Q(t)» lt = 1/Т; P(t)» 1 -lt = 1 –t /T.
Важным свойством экспоненциального распределения является вероятность безотказной работы в интервале t, t +t не зависящем от времени предшествующей работы t, а зависящей от длины интервала t.
Интервалы времени: (0, t); (0; t + t) значит P(t + t) = P(t) · P(t); - вероятность работы системы за время t при условии, что система безотказно проработала за время t.
Для экспоненциального закона ® P(t + t) = e-l(t + t); P(t) = e-lt; P(t) = e-lt.
В интервале времени (t + t) вероятность безотказной работы не зависит от времени работы t, а зависит от t.
Пример.
l = 0,01 (1/час); t = 50 (час).
 Значит: Р(50) = е-0б01 · 50 = е-0,05 = 0,0607 Т = 1/l = 100 (час).
Значит: Р(50) = е-0б01 · 50 = е-0,05 = 0,0607 Т = 1/l = 100 (час).
Распределение Рема:

d-параметр распределения Рема.
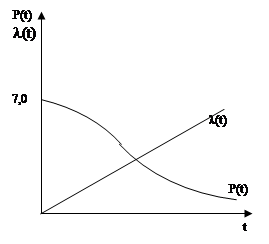 |
Пример: d = 100r, t = 50r.
P(50) = 

Нормальное распределение:

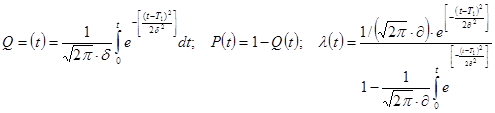

Y – распределение:

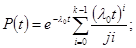

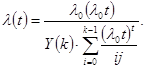
l0, к –параметр. Y-распределение.
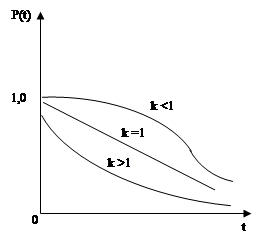 При к =1 Y параметр переходит в экспоненциальное распределение.
При к =1 Y параметр переходит в экспоненциальное распределение.
Распределение Вейбула: 
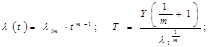
l1, m – Параметры распределения Вейбула.
 | |||
 | |||
При m =1 распределение Вейбула переходит в экспоненту; при m=2 в распределение Релея.
Появление отказов и сбоев можно представить в виде некоторого потока случайного со временем наибольшей переменной в точности получается простейший поток, который характеризуется формулой:

Эта формула позволяет рассчитать вероятность появление отказа в промежутке времени t. Простейший поток характеризует три свойства времени: стационарностью, отсутствием последействия, ординарностью.
Стационарность - указывает, что вероятность появления определенного числа событий за заданный период, времени который не зависит от положений этого периода на оси времени, а зависит только от его действительности.
|
|
|
Отсутствие последействия – характерно тем, что вероятность появления определенного числа событий за заданный период времени независящий от числа и характеризующий события, происходящие до этого времени.
Ординарность - означает не возможность одновременного появления двух и более событий.
Простейший поток получается если:
 l(t) = l =cons t; P(t) =e-lt;
l(t) = l =cons t; P(t) =e-lt;
С экспоненциальным законом хорошо согласуются законы распределения отказов для сложных систем, состоящих из многих элементов.
Это объясняется тем, что закон распределения интервалов м/д соседними событиями в потоке редких случайных событий составленных из многих неизвестных потоков с любыми характеристиками, которые сходятся к экспоненциальному закону.

|
 |
(0, t1) - первый период повышенных интенсивных отказов. Это связано с выявлением дефектов при изготовлении.
(t1, t2) – второй период, характеризующий постоянные значения интенсивных отказов. Это участок нормальной эксплуатации изделия.
(t2, ¥) Третий период, характеризующий повышенную интенсивность отказов. Здесь начинается процесс старения.
Второй период характеризует эксплуатацию и распределение.
Первый и третий период характеризует распределение Вейбула.
При m < 1 распределение Вейбула можно использовать для оценки надежности изделий при наработке стажа по прошествии времени.
Методы расчета надежности.
Для расчета надежности радиоэлектронной аппаратуры в зависимости от ее надежности (не восстанавливаемость и восстанавливаемость), все зависит от режима обслуживания, от условий хранения, от структуры использования различных методов расчета надежности.
Различные методы для расчета надежности системы с учетом восстановления и без учета восстановления.
Для расчета надежности без учета восстановления используется два метода: графовероятностный и логико-вероятностный. Прежде всего, необходимо определить критерии отказа сбоя систем.
Критерии отказа систем являются нарушением способности этой системы выполнять свое назначение, при этом могут не соответствовать выходные параметры и будут применены какие от действия по известным нормам.
При создании математической модели структуры технической системы выявятся ее критерии, при которых определяется состояние элементов составляющих данную систему. В этом случае каждый из элементов может находиться в двух состояниях работоспособном и неработоспособном. Второе состояние выражает отказ системы. Состояние системы определяется совокупностью состояния ее элементов. Критерии отказа позволяют все множество элементов разделить на два подмножества
1) Характеризует состояние работоспособности системы.
2) Состояние отказа.
Для сложной структуры анализ надежности системы сводится к представлению системы в виде некоторого элемента.
Графовероятностный метод. Основывается на представлении схемы расчета надежности в виде связного двухполюсного графа, имеющего два полюса: входной и выходной. Физически это можно представить как определение возможности прохождение некоторого сигнала от входа некоторой системы характерной сетевой структуры, к выходу.
Схемы распределения надежности различают по критерию работоспособности или отказа. Всевозможные структуры систем можно свести к последовательным и комбинированным.
Последовательные системы называются системы, которые работоспособны тогда, когда работоспособны все ее элементы. Если говорить о состоянии отказа, то последовательные системы отказывают, если отказывает хотя бы один ее элемент.

 Обозначим:
Обозначим:  n – число элементов в последовательной системе, а событие состояний в работоспособной 8 – го элемента через х8, а событие состояний b работоспособность всей системы через s, тогда схема расчета надежности по критерию работоспособности и отказа и по дереву работоспособности и отказа будут иметь следующий вид: в дереве работоспособности базисное событие, определяемое работоспособность элементов х8, связано между собой логическими звеньями, а в дереве отказов базисное событие, определяемое, отказами элементов х8 связано между собой логическими звеньями или (v) ® схема расчета по критерию работоспособности изображена ниже:
n – число элементов в последовательной системе, а событие состояний в работоспособной 8 – го элемента через х8, а событие состояний b работоспособность всей системы через s, тогда схема расчета надежности по критерию работоспособности и отказа и по дереву работоспособности и отказа будут иметь следующий вид: в дереве работоспособности базисное событие, определяемое работоспособность элементов х8, связано между собой логическими звеньями, а в дереве отказов базисное событие, определяемое, отказами элементов х8 связано между собой логическими звеньями или (v) ® схема расчета по критерию работоспособности изображена ниже:


Схема распределения по критерию отказа.Схема расчета по дереву работоспособности.
 |

Схема расчета по дереву отказа.
 На рисунках соединены исходный узел А узлом Е расчеты, на схеме расчет надежности существует тогда, когда работоспособны все ее элементы. Из рисунка б) видно, что система отказывает, если хотя бы 1 элемент, поэтому начальные и конечные сигналы всех веток должны совпадать с начальным узлом системы А и конечным Е. Все события на рисунках представляют схему со включенными элементами.
На рисунках соединены исходный узел А узлом Е расчеты, на схеме расчет надежности существует тогда, когда работоспособны все ее элементы. Из рисунка б) видно, что система отказывает, если хотя бы 1 элемент, поэтому начальные и конечные сигналы всех веток должны совпадать с начальным узлом системы А и конечным Е. Все события на рисунках представляют схему со включенными элементами.
Надежность последовательной системной оценки определяется формулой: 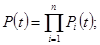
Где Pi(t) коэффициент надежности. I – его элементная система.
Параллельные системы.
Называется такая система, которая работоспособна, если работоспособен хотя бы 1 из ее элементов, т.е. система отказывает тогда, когда отказывают все элементы. События состоят в том, что восьмой элемент работоспособен обозначим его как х8 где х8 = 1, 2…, n, n – число в системе. События состояния отказа s, тогда схема работоспособна и расчет по критерию работоспособности и отказа будет иметь следующий вид:
Схема расчета по критерию работоспособности.
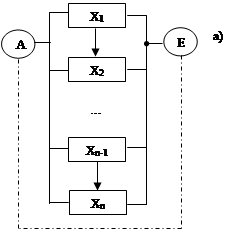 Схема расчета по критерию отказа.
Схема расчета по критерию отказа.
 |
Схема расчета по дереву работы.
 |
Отказ.


где Pi(t) –надежность i- того элемента.
Вторая формула пригодна для равно наделенных элементов.
Надежность системы с последовательно параллельной структурой.
Для последовательно параллельной структуры эффективным является метод свертки. Он основан на поэтапном преобразовании этой структуры в последовательные структуры.
 | |||
 | |||
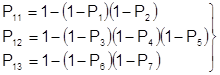 ;
;  ;
;
Метод свертки.
Схема мажоритарного регулирования
 |

 P31 = 1 –(1 – P2)(1 – P22) ==>
P31 = 1 –(1 – P2)(1 – P22) ==>
P = (P11 · P31 · P10)

 На выходе получается тот же сигнал большинство которых Р0. Если РР0 =1 то: получим две схемы.
На выходе получается тот же сигнал большинство которых Р0. Если РР0 =1 то: получим две схемы.

Не все схемы надежности можно представить в виде комбинации последовательной и параллельной. Поэтому для расчета схем используют приближенные методы.

Метод минимальных путей и сечений.
Минимальным путем называется такой j - минимальный путь, который состоит из min совокупности m подсистем, необходимый для безотказной работы системы независимо от состояния остальных подсистем.
В структуре системы есть несколько min путей. Характерным признаком min пути является то, что отказ хотя бы одной подсистемы (если работоспособна только подсистема одного пути) влечет за собой отказ системы.
Минимальное сечение это такое сечение k – min сечения, которое состоит из минимальной совокупности подсистемы Nk, чей одновременный отказ влечет за собой отказ системы независимо от состояния остальных подсистем.
Характерный сбой min сечения является то, что восстановлен хотя бы первая подсистема в min сечении (если остальные подсистемы работают) влечет за собой восстановление подсистемы.
Min сечения: 513, 524, 5164.
По методу min путей и сечений можно получить только оценки PH и РВ т.е. вероятности безотказной работы системы соответствует снизу и сверху
РН £ РС £ РВ.
Вероятность РН выражается как вероятность безотказной работы вспомогательной системы, составленной из последней включенной группы подсистем соответственно min сечениями системы.
Каждая группа состоит параллельно включенных подсистем соответственно min сечения. Вероятность выражений, как вероятность безотказной работы вспомогательных систем, составленной из последней включенной группы подсистем соответственно, если min путям системы.
Каждая группа состоит из последовательных включенных подсистем соответственного минимального пути.
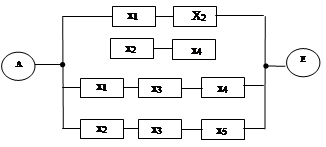
 Эквивалентная схема min пути
Эквивалентная схема min пути
 по критерию работоспособности.
по критерию работоспособности.

Минимальный путь определяет РВ, минимального сечения – РН.

РН = [1 – (1 – P)2] [1 – (1 – P)3]2» 0,97814 Если Р = 0,9.
 | |||
| |||
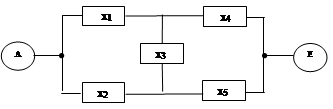
Методы исключения элементов.
 | |||
| |||
Сущность этого метода заключается в том, из структурной схемы выбрасывается 1 или несколько элементов и затем производится расчет показателя надежности для 2-х крайних случаев. В одном случае предполагается, что выбрасываемые элементы надежны (Р = 1), во 2 – м не надежны (Р = 0).
В 1 – м случае 2 – е точки схемы, к которым подключены элементы, которые соединяются постоянной связью, во втором связь м/д этими точками отсутствует.
Для этих двух вырожденных структур определить вероятность безотказной работы соответствует Pmax и Pmin, затем определяем взвешенность значений вероятности безотказной работы исключаемых элементов:  Pi – вероятность безотказной работы i – го элемента. n – число исключенных элементов.
Pi – вероятность безотказной работы i – го элемента. n – число исключенных элементов.
Окончательная вероятность безотказной работы структурной схемы определяется по следующим формулам:
(надежность системы) РС = Рmin + (Pmax – Pmin) Pср.
Если Рср = 1(надежный элемент), то Рс = Рmax 
Если Рср = 0(не надежный элемент), то Рс = Рmix 
 | |||
 | |||
Логико-вероятностный метод.
Он состоит из представления состояния каждого компонента изделия в виде булевой переменной. Одни компоненты работоспособны, а другие в состоянии отказа.
Для работоспособного изделия в целом строится таблица истинности, которая состоит из 2n строк, где n – число компонентов изделия. Из таблицы истинности записывается булевская функция работоспособности в СДНФ.
Следующим этапом является переход (запись булевской функции как вероятностную), т.е. из СДНФ можно перейти к вероятностной. 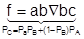 .
.
Существуют несколько форм преобразования форм функции из СДНФ либо ОДНФ (нормальная ортогональная дизъюнктивная форма), либо в ДНФ. Из этих форм можно сразу переходить к вероятностям.
ОДНФ является такой формой ДНФ, члены которой попарно ортогональны. Каждую пару элементарной конъюнкции zi и zj всегда входят некоторые ха, причем в одну из конечных инверсий, а в другую без инверсий.





 ОДНФ: u(х) = х1х2 v х1х2х3 v х1х2х4 не ОДНФ: u(х) = х1х2 v х1х3х4 Повторной формой булевой функции называется такое ее представление, когда элементарная конъюнкция булевской функции не содержит одноименных переменных.
ОДНФ: u(х) = х1х2 v х1х2х3 v х1х2х4 не ОДНФ: u(х) = х1х2 v х1х3х4 Повторной формой булевой функции называется такое ее представление, когда элементарная конъюнкция булевской функции не содержит одноименных переменных.



 Функция u(х) = (х1х2vх3)х4vх5 задана дизъюнктивной бесповторной формой. Используя правило Де Моргана можно получить конъюнктивной бесповоротной формы:
Функция u(х) = (х1х2vх3)х4vх5 задана дизъюнктивной бесповторной формой. Используя правило Де Моргана можно получить конъюнктивной бесповоротной формы:

 u(х) = х1х2х3х4х5.
u(х) = х1х2х3х4х5.
Логико-вероятностный метод является точным методом оценки надежности в отличии от графического.
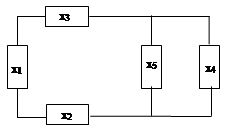
Логико-вероятностный метод.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
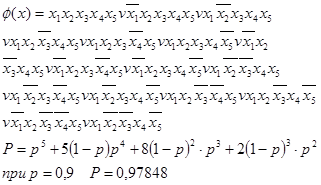

Методы расчета надежности для систем с восстановлением.
Метод расчета надежности с использованием теории Марковских процессов.
Пусть имеется некоторая система s. Говорят, что в s происходит случайный процесс, если он к стечением времени под влиянием случайных факторов (например, отказов и восстановлений отдельных компонентов) переходит из одного состояния в другое.
Такая система называется с дискретным состоянием, если она имеет конечное количество возможных состояний и переход из одного состояния в другое осуществляется скачком. Для описания случайного процесса, проистекающего в системе пользователя вероятностями состояний Р0(t), P1(t) …Pk(t) где Pi(t) (i=0,…k) – вероятность того, что система в момент t находится в состоянии si. 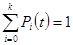
Случайный процесс, протекающий в s называется процессом в дискретном времени, если переходы из одного состояния возможны в определенные периоды времени. Если переходы возможны в любой момент времени, то процесс называется непрерывным.
Случайный процесс называется Марковским (если процесс без последствия) если все Р. процесса в будущем зависят от того, в котором состоянии находится процесс настоящем, и не зависят от того, каким образом этот процесс протекал в прошлом.
Марковский процесс представляет собой Марковскую цепь с k – различным состоянием и может быть предоставлен матрицей значений переходных вероятностей.

Марковская цепь в состоянии i на очередном шаге перейдет в состояние j. Переход вероятности не зависит от номера шага, т.е. процесс перехода стационарен во времени то есть Марковская цепь является дискретным случайным процессом с дискретным временем из которого переход осуществляется через некоторый интервал времени D t из одного состояния в другое счетное число состояний. Длительность пребывания в состоянии si является случайной величиной для которого Fk(t) состояний. Все распределения Fk(t) подчинены экспоненциальному закону.
Марковский процесс обладает характерными свойствами, определенными в первую очередь экспоненциальными распределениями времени пребывания в каждом состоянии.
1) Марковский процесс обладает свойством стационарного перехода в другую вероятность и длительность пребывания в том или ином состоянии не зависит от того в какой момент времени рассматривается этот процесс.
2) Свойство оригинальности - за бесконечный промежуток времени не может произойти более одного перехода из одноного состояния в другое.
3) Обладает свойством последствия.
Марковский процесс удобно описывать ориентировочно графом переходов вершины которого, представляют собой состояние, а) веса ребер соответствующих интенсивности перехода из одного состояния в другое. Зная переходную вероятность Pij и параметр li распределение времени пребывания процесса в i состоянии можно легко найти веса по формуле: lij = Pij · li.
Если при описании процесса перехода система из одного состояния в состояние сохраняет Марковское свойство, то пребывание Fk(t) подчиняется произвольному, не экспоненциальному закону, то такой процесс называется полумарковским или неоднородным Марковским процессом.
На основании графических переходов можно составить дифференциальные уравнения для нахождения вероятности пребывания Марковского процесса в состоянии Pi.
1) Производная по t от пребывания системы в момент t в состоянии Pi равна сумме произведений интенсивности переходов на составляющую вероятность. При этом слагаемым которые, соответствуют выходящим из одного состояния стрелки в другое приписывается знак “–”, а остальные состояния “+”. Общее число слагаемых равно числу входящих и выходящих.
Система дифференциальных уравнений содержит k – уравнений, но они зависимы, поэтому нужно дополнить их уравнением нормировки, которое показывает, что сумма событий полную группу равна 1.
Различают два типа случайных процессов:
а) при первом попадании в нерабочее состояние процесс прекращается (процесс с поглощающим экраном).
в) система находится в стационарном режиме отказов (с отражающим экраном).
Первый случай для не восстановимого изделия, а второй для изделия которое можно восстановить.
P1(t) – состояние работоспособности изделия.
Р2(t) – состояние отказов
l и m интенсивност
|
|
|


