 |
Вероятностное описание результатов и погрешностей.
|
|
|
|
Если при повторных измерениях одной и той же физической величины, проведенных с одинаковой тщательностью и в одинаковых условиях получаемые результаты, отличаются друг от друга, то это свидетельствует о наличии случайных погрешностей. Случайные погрешности являются результатом одновременного воздействия на измеряемую величину многих случайных возмущений. Предсказать результат наблюдения или исправить его введением поправки невозможно. Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится в пределах разброса результатов наблюдений от xmin до xmax, где xmin, xmax – соответственно, нижняя и верхняя границы разброса.
Однако остается неясным, какова вероятность появления того или иного значения погрешности, какое из множества лежащих в этой области значений величины принять за результат измерения и какими показателями охарактеризовать случайную погрешность результата. Для ответа на эти вопросы требуется принципиально иной, чем при анализе систематических погрешностей, подход. Подход этот основывается на рассмотрении результатов наблюдений, результатов измерений и случайных погрешностей как случайных величин. Методы теории вероятностей и математической статистики позволяют установить вероятностные (статистические) закономерности появления случайных погрешностей и на основании этих закономерностей дать количественные оценки результата измерения и его случайной погрешности.
Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии преимущественно используется дифференциальная форма – закон распределения плотности вероятностей случайной величины.
|
|
|
20) На рис. 1 показана полученная в одном из опытов гистограмма, построенная на основании результатов 100 наблюдений, сгруппированных в таблице 1.
Таблица 1

В данном опыте в первый и последующие интервалы попадает соответственно 0,06; 0,12; 0,18; 0,25; 0,17; 0,14 и 0,08 от общего количества наблюдений; при этом, очевидно, что сумма этих чисел равна единице.

Рис. 1. Гистограмма
Если распределение случайной величины х статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины, в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Это означает, что построив гистограмму один раз, при последующих сериях наблюдений можно с определенной долей уверенности заранее предсказать распределение результатов наблюдений по интервалам. Приняв общую площадь, ограниченную контуром гистограммы и осью абсцисс, за единицу, S0 =1, относительную частоту попаданий результатов наблюдений в тот или иной интервал можно определить как отношение площади соответствующего прямоугольника шириной Δl к общей площади.
При бесконечном увеличении числа наблюдений n→ ∞ и бесконечном уменьшении ширины интервалов Δl →0, ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую f (x) (рис. 2), называемую кривой плотности распределения вероятностей случайной величины, а уравнение, описывающее ее, – дифференциальным законом распределения. Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде
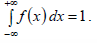
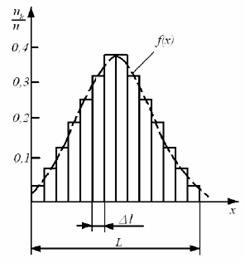
Рис. 2. Кривая плотности распределения вероятностей
Закон распределения дает полную информацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности. Если известен дифференциальный закон распределения f (x), то вероятность Ρ попадания случайной величины х в интервал от x1 до x2 можно записать в следующем виде
|
|
|
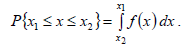
Графически эта вероятность выражается отношением площади, лежащей под кривой f (x) в интервале от x1 до x2 к общей площади, ограниченной кривой распределения. Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величины х в интервал [− ∞; + ∞] равна единице, т.е. представляет собой достоверное событие. Вероятность этого события называется функцией распределения случайной величины и обозначается F(x). Функцию распределения F(x) иногда называют также интегральной функцией распределения. В терминах интегральной функции распределения имеем
P {x1 ≤ x ≤ x2} = F (x1)− F (x2),
т.е. вероятность попадания результата наблюдений или случайной погрешности в заданный интервал равна разности значений функции распределения на границах этого интервала.
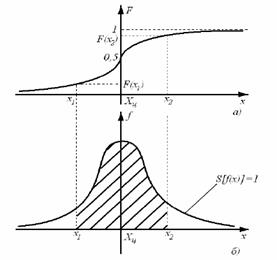
Рис. 3. Интегральная (а) и дифференциальная (б) функции распределения случайной величины
Интегральной функцией распределения F(x) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина xi в i -м опыте принимает значение, меньшее х. График интегральной функции распределения показан на рис. 3, а. Она имеет следующие свойства:
− неотрицательная, т.е. F(x) ≥ 0;
− неубывающая, т.е. f (x2) ≥ F(x1), если x2 ≥ x1;
− диапазон ее изменения: от 0 до 1, т.е. F(−∞) = 0; F(+∞) = 1;
− вероятность нахождения случайной величины х в диапазоне от x1 до
x2: P{x1 < x < x2}= F(x2) − F(x1).
Запишем функцию распределения через плотность:

Площадь, ограниченная кривой распределения, лежащая левее точки x – текущая переменная) (рис. 4), отнесенная к общей площади, есть не что иное, как интегральная функция распределения F(x) = P{xi < x}. 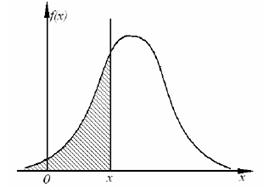
Рис. 4. Кривая плотности распределения вероятностей (дифференциальная функция распределения случайной величины)
Плотность распределения вероятностей f (x) называют
дифференциальной функцией распределения:
|
|
|
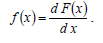
Пример распределения дискретной случайной величины приведен на рис. 5.

Рис. 5. Распределение дискретной случайной величины
21) Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Например, денежный выигрыш в какой-нибудь лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством)
Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.
Закон распределения дискретной случайной величины представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σpi = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (xi; pi)
Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x:
F(X) = P(ξ < X).
Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины.
|
|
|


