 |
Принцип Ферма. Закон преломления. Закон отражения.
|
|
|
|
Согласно принципу Ферма: луч света распространяется по пути, время прохождения по которому минимально. Принцип Ферма легко объясняет прямолинейность распространения света в однородной среде. Так как в однородной среде скорость света всюду одинакова, а значит минимальное время будет определяться кратчайшим путем, то есть между двумя точками – это отрезок. Рассмотрим как исходя из этого принципа можно получить закон отражения и закон преломления.
Пусть свет от точечного источника S, отразившись от границы двух сред, попадет в точку А.
| 
|
Так как свет распространяется в одной и той же среде, то время будет минимально, когда будет минимален путь. Значит надо найти на границе точку O такую, что SO + OA минимальна.
Закон преломления:
| 
|
Чтобы найти при каком наклоне х время t будет минимальным, надо взять производную
Преломление лучей в треугольной призме.
Пусть треугольная призма сделана из материала с показателем преломления n2 и находиться в среде с показателем n1.
Рассмотрим для первого случая, каким будет угол, на который отклоняется луч от первоначального направления.
Угол между двумя гранями призмы, на который происходит преломление – преломленный угол призмы.
|
|
|
|
|
|
|
|
|
|
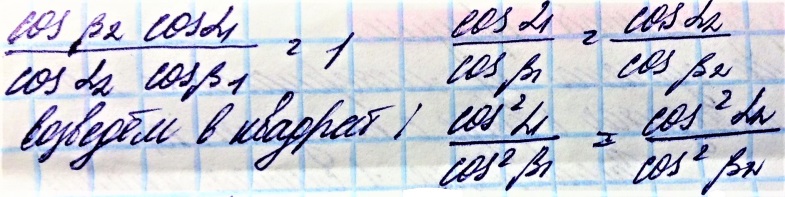
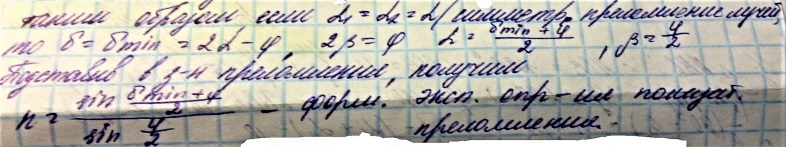
10. Преломление света на сферическую поверхность. Инвариант Аббе.
Рассмотрим преломление света на сферическую границу двух сред с абсолютными показателями преломления n1 и n2.
Луч SP падает на поверхность перпендикулярно, следовательно, не преломляется и проходит через центр кривизны поверхности C. Луч SA преломляется в точке А и пройдет через точку SI. Если положение этой точки не будет зависеть от угла фи, то все лучи, выходящие из S, попадут в SI. То есть SI будет в этом случае изображением. Будем считать, что угол фи и угол падения a (альфа) малы, тогда точка Р и то точка В будут настолько близки друг другу, что их можно считать совпадающими.
|
|
|
Для того, чтобы рассмотреть вогнутой поверхности (выпуклой поверхности), воспользуемся принципом обратимости лучей: при изменении направления лучей на обратное, при преломлении и отражении взаимное расположение лучей не меняется.
Этот принцип действителен при любом числе отражений и преломлений. Если представить, что свет идет от источника SI, то луч пойдет по пути SIAS и тогда, заменив S на SI, a1 на a2, и n1 на n2, получим:
Таким образом, с учетом знаков расстояние a1, a2, R можно утверждать, что при преломлении на сферической поверхности произведение 
сохраняет свою величину. Это выражение называется инвариантом Аббе, точнее первым инвариантом Аббе. Законы отражения и преломления также можно объединить, если при отражении считать, что
Отражение в сферических зеркалах.
В качестве примера использования инварианта Аббе, рассмотрим отражение в сферическом зеркале. Перепишем инвариант Аббе для двух сред в следующем виде:
|
|
|
Формула тонкой линзы.
Линза - это прозрачное тело с определенным показателем преломления n, ограниченное двумя сферическими поверхностями.
Линия, проходящая через центр кривизны обоих поверхностей, называется главной оптической осью.
Построение изображений в линзе.
Собирающая линза:
Рассеивающая линза:
1) Строиться побочная ось параллельно падающему лучу
2) Через F параллельно линзе – фокальная плоскость
Построение произвольного луча основано на том факте, что параллельный пучок, лучей, идущий под углом к главной оптической оси тоже собирается в одной точке, но не фокусе, а в плоскости параллельной линзе, проходящей через фокус.
|
|
|
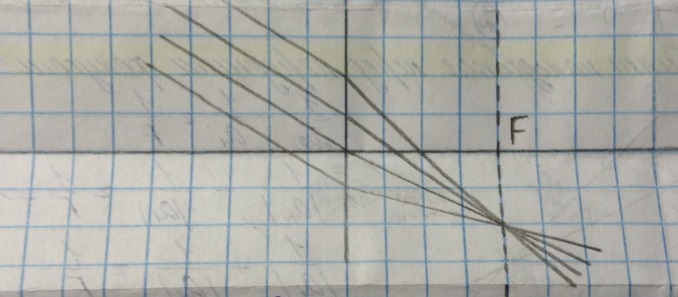
Для рассеивающей линзы
Увеличение линзы.
Различают линейное и угловое увеличение, а линейное бывает поперечным и продольным.
Линейное поперечное увеличение
Угловое увеличение
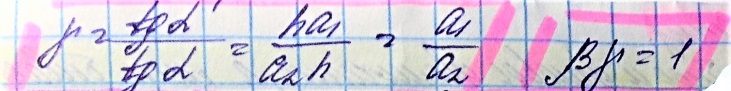
Линейное продольное увеличение
Дефекты линз.
1) Если на собирающую линзу направить параллельный пучок лучей, то они соберутся в фокусе, но это факт следует для параксиальных лучей, для которых угол падения на поверхность линзы настолько мал, что sin a = a. В реальной линзе это условие выполняется для лучей в близи главной оптической оси. Для лучей, далеких от главной оптической оси тогда sin a < a.
Значит, лучи отклоняются сильнее, чем параксиальные и пересекают оптическую ось ближе, чем в фокусе.
Максимальное расстояние будет для крайнего луча, который определяет отрезок б, называемый мерой сферической аберрацией. Для собирающей линзы б >0, то есть смещение происходит против хода луча. Для рассеивающей линзы б <0, то есть смещение происходит по ходу лучей. Сферическая аберрация проявляется в размытости фокуса вдоль главной оптической оси, что приводит к размытости изображения. Для уменьшение этого дефекта можно: диафрагмировать пучок, калибровать собирающую или рассеивающую линзу.
2) Астигматизм – Если точечный источник света находиться не на главной оптической оси, то лучи, идущие в сторону линзы, образуют пучок, волновой фронт которого является сферическим. После преломление в линзе, волновые поверхности становятся не сферическими. Поэтому преломленные лучи сходятся не в одной точке. Это приводит в случае действительного изображения к тому, что на разном удалении от линзы четкими будут разные элементы изображения.
Если расположить экран в плоскости 1, изображение точки S превратиться в горизонтальный отрезок, если в плоскости 3, то получиться вертикальный отрезок. Наиболее приемлемый вариант расположение экрана в плоскости 2, тогда изображение точки S будет размытым овалом. Например, если в качестве объекта взять и разместить его центр на главной оптической оси, то в плоскости 1 получим четкие окружности размытые отрезки, а в плоскости 2 – наоборот.
3) Кома. Если святящееся точка посылает широкий пучок и находиться вне главной оптической оси, ее изображение может представлять собой неравномерное освященное пятнышко, представляющая собой комету с хвостиком.
|
|
|
4) Дисторсия – неодинаковость поперечных увеличений для объектов разной угловой величины, приводят к искажениям, которые меняют изображение от центра к периферии.
5) Хроматическая аберрация.
|
|
|
