 |
смо смешанного типа с ограничением времени ожидания в очереди
|
|
|
|
Рассмотрим СМО с п каналами. На вход системы поступает простейший поток заявок с плотностью l. Время ожидания заявки в очереди Тож распределено по показательному закону со средним значением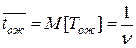 
. Время обслуживания показательное со средним значением 
. Параметр n полностью аналогичен параметрам l и m. Его можно интерпретировать, как плотность «потока уходов» заявки, стоящей в очереди.
Пусть максимальное число мест в очереди ограничено и равно т.
В этом случае система имеет т + n + 1 состояние. Размеченный граф состояний выглядит так:
Можно составить уравнения, аналогичные уравнениям Эрланга для предельного стационарного режима при t ® ¥ вероятности состояний, полученные из этих уравнений запишутся так:
, (6.1)
, (6.2)
где 
.
Параметры a и b выражают соответственно среднее число заявок и среднее число уходов заявки, стоящей в очереди, приходящиеся на среднее время обслуживания одной заявки. Данные формулы достаточно громоздки и требуют большой вычислительной работы. Поэтому их можно записать в другом виде:
(6.3)
(6.4)
где 
Если d не является целым, то вычисление можно провести для двух ближайших к величине d целых числе и произвести между ними линейную интерполяцию.
Средне число занятых каналов определяем по формуле:
(6.5)
Вероятность обслуживания заявки Робс = 
.
Если число мест в очереди не ограничено (т ® ¥), то формулы упрощаются с учетом того, то 
.
Если заявки, попавшие в очередь, не покидают ее, а терпеливо дожидаются обслуживания (n = 0, а значит, и b = 0), то формулы (6.1) и (6.2) превращаются в формулы (5.1), (5.2), которые мы рассматривали в § 5).
Если при этом длина очереди не ограничена (т ® ¥), то получим формулы (4.1), (4.2), мак как система превращается в чистую систему с ожиданием (см. § 4).
|
|
|
Задача 1. В магазине обслуживают покупателей четыре продавца. Среднее время обслуживания одного покупателя 4 мин. Плотность потока покупателей около двух человек в минуту. В очереди могут ожидать одновременно не более 20 человек. В среднем покупатель, вставший в очередь, ожидает 10 мин., после чего он покидает магазин.
Определить: 1) среднее число занятых продавцов;
2) среднее число покупателей, ожидающих в очереди;
3) вероятность того, что все места в очереди будут заняты;
4) вероятность того, что покупатель будет обслужен;
5) среднее время пребывания в очереди;
6) среднее время, затачиваемое на всю процедуру (ожидание в очереди и обслуживание).
Решение. Работа магазина может быть представлена как работа СМО смешанного типа. Параметры этой системы следующие:
п = 4 – число каналов обслуживания;
т = 20 – максимальное число мест в очереди;
– среднее число покупателей, приходящих в магазин;
– среднее время обслуживания одного покупателя 
;
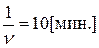– среднее время ожидания покупателя в очереди. После чего он покидает магазин 
;
; 
; 
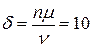– целое число.
1) Среднее число занятых продавцов:
то есть практически все продавцы будут заняты.
2) Среднее число покупателей, ожидающих в очереди:
3) Вероятность того, что все места в очереди будут заняты:
то есть все места в очереди будут заняты с вероятностью менее 1 %.
4) Вероятность обслуживания:
6) Среднее время, затачиваемое на всю процедуру:
Задача 2. С целью увеличения дальности беспосадочного полета производится дозаправка самолетов горючим в воздухе. В районе дозаправки постоянно дежурят четыре самолета-дозаправщика. Если дозаправка началась, то она осуществляется до конца и длится в среднем 10 минут. Если все дозаправщики заняты, то самолет, нуждающийся в дозаправке, может некоторое время «ожидать» (совершать полет по кругу в районе дозаправки); среднее время ожидании 20 минут. Если самолет не дождался дозаправки в воздухе, он садится на запасной аэродром. Интенсивность полетов такова, что в среднем за час в район дозаправки прибывает 24 самолета. Число самолетов, ожидающих дозаправки в воздухе, не ограничено.
|
|
|
Определить: 1) вероятность Робс того, что самолет будет дозаправлен;
2) среднее число занятых дозаправщиков;
3) вероятность того, что произвольно взятый дозаправщик будет занят;
4) среднее время простоя дозаправщика.
Решение. Рассматриваемая система может быть рассмотрена как СМО смешанного типа с параметрами:
число каналов обслуживания п = 4;
число мест в очереди не ограничено (т ® ¥);
плотность потока заявок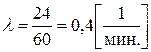 
;
плотность потока обслуживаний 
;
плотность потока уходов из очереди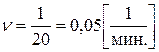 
.
Отсюда 
– целое число.
По формуле (6.5) находим среднее число дозаправщиков, занятых обслуживанием самолетов:
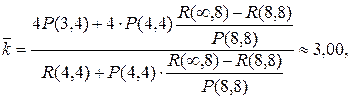
где R (¥;8) = 1.
Вероятность тог, что самолет будет дозаправлен:
Среднее время простоя дозаправщика:
Задачи.
1. Гарантийная мастерская принимает заказы на ремонт по одному телефону. Среднее число заказов за 1 час – 2 п. Среднее время оформления заявки т мин. Считается, что если клиент позвонил, а телефон занят, то он обратится в другую мастерскую (система без очереди). Найти основные характеристики СМО: 1) р 0, р 1; 2) робс; 3) 
; 4) 
. Проанализировать, как изменятся соответствующие показатели, если подключить второй телефон. С какой интенсивностью должны работать два работника, чтобы доля потерь заявок была менее 10 %?, менее 5 %?
2. В мастерской по ремонту холодильников имеются 3 мастера. Мастер в среднем может отремонтировать 1 холодильник за 80 минут. Рабочий день составляет 8 часов. В мастерскую в среднем поступает 40 заявок на ремонт за рабочий день. В случае, если все мастера заняты, холодильник в ремонт не принимается (СМО с отказом). Заработная плата мастеров почасовая,
150 рублей в час. Клиент в среднем платит за ремонт 300 рублей (запчасти оплачиваются отдельно). Определить чистую прибыль мастерской за смену. Как изменится прибыль, если пригласить в мастерскую 4-го мастера? Определить количество мастеров, при котором прибыль мастерской максимальна.
3. В платной справочной телефонной службе имеется четыре телефонные линии. В справочную поступает простейший поток заявок со средней интенсивностью 1 заявка в 2 минуты. Ответ на каждый вопрос длится в среднем 6 минут. За ответ на каждый вопрос клиент платит 10 руб.. Эксплуатация одного канала обслуживания составляет 30 руб./час, создание канала обслуживания требует расхода 8000 руб. Определить чистый доход за один час. Через сколько часов произойдет окупаемость системы?
|
|
|
4. Гарантийная мастерская принимает заказы на ремонт по одному телефону. Среднее число поступающих в течение часа заказов – 20, среднее время оформления заказа – 4 минуты. Определить показатели СМО:
1) вероятности состояний системы р 0, р 1; 2) вероятность обслуживания заявки робс; 3) среднее число занятых каналов ; 4) вероятность занятости канала; 5) среднее время простоя канала. Проанализировать, как они изменятся, если подключить второй телефон.
5. Средний интервал между поступающими в прокатный пункт заявками и запросами на наличие определенных предметов составляет 5 мин. Принимают заявки два работника, каждый с интенсивностью 12 заявок в час. С какой интенсивностью должен работать один работник, выполняя работу двух, чтобы доля потерянных требований осталась на прежнем уровне? На сколько требуется повысить интенсивность обслуживания двум работникам, чтобы доля потерянных заявок была менее 10 %?
6. На диспетчерском пункте дежурят 4 приемщика заявок на ремонт телерадиоаппаратуры. Заявки принимаются по телефону. В диспетчерский пункт поступает простейший поток заявок с плотностью l = 3 (заявки в минуту). Вызов, поступивший в момент, когда все приемщики заняты, получает отказ. Средняя длительность оформления заявки 2 минуты. Найти все характеристики СМО: 1) вероятности состояний системы р 0, р 1;
2) вероятность обслуживания заявки робс; 3)среднее число занятых каналов ; 4) вероятность занятости канала; 5) среднее время простоя канала.
С какой интенсивностью должны работать 2 работника, выполняя работу четырех, чтобы доля потерянных требований осталась на прежнем уровне?
|
|
|
7. Библиотека принимает заявки на книги по одному телефону. Среднее число поступающих в течение часа заявок – 70, среднее время оформления заявки – 2 минуты. Определить показатели СМО (задача 6). Найти, как изменятся параметры системы, если заявки будут приниматься по двум телефонам и при этом доля потерянных заявок уменьшится в 2 раза по сравнению с прежним уровнем. Как изменится время пребывания заявки в системе?
8. Пусть в СМО с отказом поступает в среднем 15 заявок в час. Среднее время обслуживания заявки составляет 12 мин. За обслуживание заявки клиент платит 80 рублей. Содержание одного канала обслуживания обходится 100 рублей в час. Определить число каналов обслуживания, при которых прибыль максимальна.
Литература
1. Венцель Е.С. Теория вероятностей. М., 1962.
2. Венцель Е.С., Овчаров Л.А. Теория вероятностей. М., 1969.
3. Гнеденко Б.В. Лекции по теории массового обслуживания. Изд. КВИРТУ, 1960.
4. Н.Ш.Кремер Теория вероятностей и математическая статистика. Учебник. 2-е издание. Москва, 2003, 2006 ЮНИТИ.
|
|
|
