 |
Вписанные и описанные фигуры.
|
|
|
|
В8 все задачи из банка
Площади поверхности
Параллелепипед
27143. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
27128. Рёбра прямоугольного параллелепипеда равны 1, 2, 3. Найдите площадь его поверхности.
27067. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.

Многогранники
25541 25561 25581 25601 25621





25641 25661 25681 25701 25721




25881 27071 77155 77156 77157





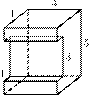
27158. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Куб
27055 Площадь поверхности куба равна 18. Найдите его диагональ.
27139. Диагональ куба равна 1. Найдите площадь его поверхности.
27056. Объем куба равен 8. Найдите площадь его поверхности.
27061. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
27130. Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличить в три раза?
27168. Объём первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
27075. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Призма
27132. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
27151. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
|
|
|
27062. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
27148. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
27063. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
27157. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
245356. Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней?
27065. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен  , а высота равна 2.
, а высота равна 2.

27170 Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен  , а высота равна 2.
, а высота равна 2.

245354. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
27064. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.

27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен  , а высота равна 2.
, а высота равна 2.

27057. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
27068. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

27153. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
|
|
|

Пирамида
27069. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
27155. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
27171. Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.
27070. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
27131. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
27172. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
27215. Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.

Цилиндр
27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на  .
.
27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
245358. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
284361. Площадь боковой поверхности цилиндра равна  , а диаметр основания — 1. Найдите высоту цилиндра.
, а диаметр основания — 1. Найдите высоту цилиндра.
284362. Площадь боковой поверхности цилиндра равна  , а высота — 1. Найдите диаметр основания.
, а высота — 1. Найдите диаметр основания.
316557. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
Конус
27136. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?
27137. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?
27160. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
|
|
|

27161. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсеченного конуса.
27135. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.
324458. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна  . Найдите площадь боковой поверхности конуса.
. Найдите площадь боковой поверхности конуса.

Шар
27059. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
508286. Площадь поверхности шара равна 12. Найдите площадь большого круга шара.

27072. Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
27163. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
27073. Шар вписан в цилиндр. Площадь поверхности цилиндра равна 18. Найдите площадь поверхности шара.

ОБЪЕМ
Параллелепипед
27079. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
27100. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
27041 Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
27042 Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
27103. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна  и образует с плоскостью этой грани угол 45
и образует с плоскостью этой грани угол 45  . Найдите объем параллелепипеда.
. Найдите объем параллелепипеда.
27104. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60  . Одно из ребер параллелепипеда составляет с плоскостью этой грани угол 60
. Одно из ребер параллелепипеда составляет с плоскостью этой грани угол 60  и равно 2. Найдите объем параллелепипеда.
и равно 2. Найдите объем параллелепипеда.
|
|
|
Куб
27141. Площадь поверхности куба равна 24. Найдите его объем.
27099. Объем куба равен  . Найдите его диагональ.
. Найдите его диагональ.
27098. Диагональ куба равна  . Найдите его объем.
. Найдите его объем.
27081. Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза?
27102. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
245355. Куб вписан в шар радиуса  . Найдите объем куба.
. Найдите объем куба.
27043 Куб описан около сферы радиуса 1. Найдите объём куба.
27105. Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
324449. Шар, объём которого равен  , вписан в куб. Найдите объём куба.
, вписан в куб. Найдите объём куба.
324459. Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 2. Найдите объём куба.

Многогранник
27044 27187 27188 27189 27190



27191 27192 27193



27194 27210 27211 27212 27213

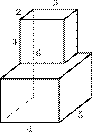




27117. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

27214. Объём тетраэдра равен 19. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.

245335. Найдите объем многогранника, вершинами которого являются точки  ,
, 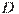 ,
,  ,
,  ,
,  ,
,  прямоугольного параллелепипеда
прямоугольного параллелепипеда  , у которого
, у которого  ,
,  ,
,  .
.
245336. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  прямоугольного параллелепипеда
прямоугольного параллелепипеда 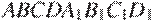 , у которого
, у которого 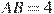 ,
,  ,
,  .
.
245337. Найдите объем многогранника, вершинами которого являются точки 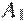 ,
,  ,
,  ,
,  ,
,  прямоугольного параллелепипеда
прямоугольного параллелепипеда  , у которого
, у которого 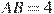 ,
,  ,
,  .
.
245338. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  прямоугольного параллелепипеда
прямоугольного параллелепипеда  , у которого
, у которого  ,
,  ,
,  .
.
245339. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  прямоугольного параллелепипеда
прямоугольного параллелепипеда 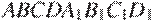 , у которого
, у которого  ,
,  ,
,  .
.
245340. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  правильной треугольной призмы
правильной треугольной призмы  , площадь основания которой равна 2, а боковое ребро равно 3.
, площадь основания которой равна 2, а боковое ребро равно 3.
245341. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  ,
,  правильной треугольной призмы
правильной треугольной призмы  , площадь основания которой равна 3, а боковое ребро равно 2.
, площадь основания которой равна 3, а боковое ребро равно 2.
245342. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  правильной треугольной призмы
правильной треугольной призмы  , площадь основания которой равна 4, а боковое ребро равно 3.
, площадь основания которой равна 4, а боковое ребро равно 3.
245343. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  ,
, 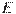 ,
,  ,
,  правильной шестиугольной призмы
правильной шестиугольной призмы  , площадь основания которой равна 4, а боковое ребро равно 3.
, площадь основания которой равна 4, а боковое ребро равно 3.
|
|
|
245344. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  ,
,  ,
,  правильной шестиугольной призмы
правильной шестиугольной призмы  , площадь основания которой равна 6, а боковое ребро равно 3.
, площадь основания которой равна 6, а боковое ребро равно 3.
245345. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 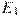 правильной шестиугольной призмы
правильной шестиугольной призмы  , площадь основания которой равна 6, а боковое ребро равно 2.
, площадь основания которой равна 6, а боковое ребро равно 2.
245346. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  правильной шестиугольной призмы
правильной шестиугольной призмы  , площадь основания которой равна 6, а боковое ребро равно 2.
, площадь основания которой равна 6, а боковое ребро равно 2.
245347. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  правильной шестиугольной призмы
правильной шестиугольной призмы  , площадь основания которой равна 6, а боковое ребро равно 3.
, площадь основания которой равна 6, а боковое ребро равно 3.
Цилиндр
27051. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
27045 В цилиндрический сосуд налили  воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в
воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в  .
.

27046. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
27091. В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.
27118. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
27053. Дано два цилиндра. Объём первого цилиндра равен 12. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра.
27049. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра призмы равны  . Найдите объём цилиндра, описанного около этой призмы.
. Найдите объём цилиндра, описанного около этой призмы.

27050. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра призмы равны  . Найдите объём цилиндра, описанного около этой призмы.
. Найдите объём цилиндра, описанного около этой призмы.

245349. Шар, объём которого равен 24, вписан в цилиндр. Найдите объём цилиндра.
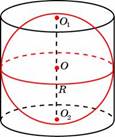
245350. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 5.
Призма
27047. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 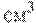 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в
воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в 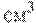 .
.

27048. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает  см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в
см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в  раза больше, чем у первого? Ответ выразите в см.
раза больше, чем у первого? Ответ выразите в см.
27106. Через среднюю линию основания треугольной призмы, объём которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объём отсеченной треугольной призмы.
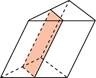
27107. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 5.
27082 (дубль). Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 6 и 8, боковое ребро призмы равно 5. Найдите объём призмы.
27083. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5, объём призмы равен 30. Найдите боковое ребро призмы.
27112. От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

27183. Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
27084. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны  .
.
27108. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны  и наклонены к плоскости основания под углом 30
и наклонены к плоскости основания под углом 30  .
.
Пирамида
27087. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна  .
.
27088. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен  .
.
27111. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

27176. Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.
27086. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
27109. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
318146. В правильной четырёхугольной пирамиде  с основанием
с основанием  боковое ребро
боковое ребро  равно 5, сторона основания равна
равно 5, сторона основания равна  . Найдите объём пирамиды.
. Найдите объём пирамиды.
27178. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
27085. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
27089. Во сколько раз увеличится объем шестиугольной пирамиды, если ее высоту увеличить в четыре раза?
27179. Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
27180. Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро
27113. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.

27114. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.

27110. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60  . Высота пирамиды равна 6. Найдите объем пирамиды.
. Высота пирамиды равна 6. Найдите объем пирамиды.

27116. Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1: 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
27074. Объем параллелепипеда  равен 9. Найдите объем треугольной пирамиды
равен 9. Найдите объем треугольной пирамиды  .
.
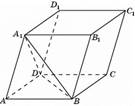
77154. Найдите объем параллелепипеда  , если объем треугольной пирамиды
, если объем треугольной пирамиды  равен 3.
равен 3.

27115. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

27182. Объем параллелепипеда  равен 12. Найдите объем треугольной пирамиды
равен 12. Найдите объем треугольной пирамиды  .
.

27209. Объем параллелепипеда  равен
равен  . Найдите объем треугольной пирамиды
. Найдите объем треугольной пирамиды 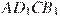 .
.

27184. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
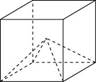
27181. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45  . Найдите объем пирамиды.
. Найдите объем пирамиды.

Конус
245351. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 28. Найдите объём конуса.
27096. Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 150. Найдите объём конуса.
27094. Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
27095. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 1,5 раза, а высота останется прежней?
318145. В сосуде, имеющем форму конуса, уровень жидкости достигает  высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

27052. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Шар
27097. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
27162. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
245352. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём конуса равен 6. Найдите объём шара.
245348. Цилиндр, объём которого равен 33, описан около шара. Найдите объём шара.

СЕЧЕНИЯ
315131. В прямоугольном параллелепипеде  ребро
ребро  , ребро
, ребро  , ребро
, ребро  . Точка
. Точка  — середина ребра
— середина ребра  . Найдите площадь сечения, проходящего через точки
. Найдите площадь сечения, проходящего через точки  ,
,  и
и  .
.
316552. В прямоугольном параллелепипеде  известны длины рёбер:
известны длины рёбер: 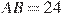 ,
,  ,
,  . Найдите площадь сечения, проходящего через вершины
. Найдите площадь сечения, проходящего через вершины  ,
,  и
и  .
.
324452. В прямоугольном параллелепипеде  известны длины рёбер:
известны длины рёбер:  ,
,  ,
,  . Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки
. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки  ,
, 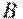 и
и  .
.

324457. В правильной четырёхугольной призме  ребро
ребро 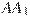 равно 15, а диагональ
равно 15, а диагональ  равна 17. Найдите площадь сечения призмы плоскостью, проходящей через точки
равна 17. Найдите площадь сечения призмы плоскостью, проходящей через точки  ,
,  и
и  .
.

324451. В правильной треугольной призме  стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер
стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер  ,
, 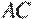 ,
,  и
и  .
.

324450. В правильной четырёхугольной пирамиде все рёбра равны 1. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.

324453. Площадь основания конуса равна 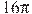 , высота — 6. Найдите площадь осевого сечения конуса.
, высота — 6. Найдите площадь осевого сечения конуса.

324455. Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
324456. Диаметр основания конуса равен 12, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
324454. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

27175. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

РАССТОЯНИЯ
Многогранники
284357. В прямоугольном параллелепипеде  известно, что
известно, что  ,
,  ,
,  . Найдите длину ребра
. Найдите длину ребра 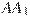 .
.
284363. В прямоугольном параллелепипеде  известно, что
известно, что  ,
,  ,
,  . Найдите длину диагонали
. Найдите длину диагонали  .
.
245366. В правильной шестиугольной призме  все ребра равны
все ребра равны  . Найдите расстояние между точками
. Найдите расстояние между точками  и
и 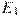 .
.
245364. В правильной шестиуголь
|
|
|


