 |
Математическое описание случайных погрешностей
|
|
|
|
Измеряемая величина это случайная величина. Наиболее общей характеристикой непрерывной случайной величины является плотность распределения её вероятности, которая определяется как
,где dF(x) – вероятность значений случайной величины x в интервале dx.
Кроме этого используется функция распределения вероятностей случайной величины
которая выражает собой вероятность того, что случайная величина находится в интервале от 
до некоторого значения <x1
Функция распределения любой случайной величины является неубывающей функцией, определенной так, что 
. Вероятность того, что случайная величина x примет значение в интервале между x1 и x2 равна
В практике электроизмерений чаще всего имеют дело с нормальным и равномерным распределениями.
Случайная величина 
распределена нормально, если её плотность вероятностей имеет вид
где 
– среднее квадратическое отклонение (СКО)
– математическое ожидание
Оценка случайных погрешностей прямых равноточных измерений
Случайные погрешности проявляются при многократных наблюдениях измеряемой величины в одинаковых условиях, их влияние на результат измерения надо учитывать и стремиться по возможности уменьшить.
К оценкам случайной величины, получаемым по статистическим данным, предъявляются требования состоятельности, несмещенности и эффективности.
Оценка параметра Q считается состоятельной, если 
, несмещенной, если 
, эффективной, если 
. Здесь 
– результат i- того наблюдения n – число наблюдений.
Способы нахождения оценок конечного ряда наблюдений и показатели их качества зависит от законов распределения.
Для нормального распределения, а если пренебречь эффективностью оценки, то и для всех симметричных распределений, в качестве оценки математического ожидания ряда равноточных наблюдений принимают среднее арифметическое ряда наблюдений.
|
|
|
При 
, если нет систематических погрешностей, 
. Разность 
представляет собой случайную погрешность при i- том наблюдении. Она может быть положительной и отрицательной.
Среднее арифметическое независимо от закона распределения, обладает следующими свойствами:
В качестве оценки дисперсии берется дисперсия отклонения результата наблюдения
А в качестве оценки СКО результата наблюдения –
Широко используется понятие максимальной погрешности, под которой понимают закон трех сигм. Так как на практике число измерений не превышает несколько десятков, то появление погрешности равно 
, маловероятно. Потому погрешность – максимальная возможная случайная погрешность. Погрешности больше считаются промахами и при обработке результатов измерений не учитываются. Схема обработки результатов измерения с многократными измерениями:
n наблюдений 
|
| Оценка закона распределения |
|
|
Исключение систематических погрешностей 
|
|
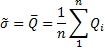
| Оценка доверительного интервала |
Запись результата 
|
Проверка
|
Остаточные погрешности 
|
|
| Выбор доверительной вероятности Р |
Суммирование погрешностей
При суммировании погрешностей пользуются:
1. Систематические погрешности 
если они известны или достаточно точно определены, суммируют алгебраически (с учетом знаков)
Рекомендуется при суммировании рассматривать все погрешности измерительной аппаратуры как случайные.
2. Случайные погрешности (среднеквадратические оценки) суммируют с учетом их взаимных коррекционных связей. Среднеквадратическая погрешность 
суммы двух случайных погрешностей характеризуемых среднеквадратичными отклонениями 
и 
,
|
|
|
Где 
Т.к. обычно информация о тесноте корреляционных связей отсутствует, то на практике рассматриваются 2 крайних случая: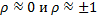 
. При этом:
· Некоррелированные (вызванные взаимно независимыми источниками или причинами) погрешности суммируются геометрически 
Если количество источников погрешностей n, то 
Где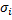 
– среднеквадратическая оценка погрешности, обусловленной -тым источником.
· Случайные погрешности, сильно или жестко коррелированные (коэффициент корреляции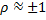 
), суммируются с учетом следующих предпосылок. Если причина вызывает в разных узлах прибора изменение погрешностей, то погрешности складываются, т. е. 
Когда же изменения получаются противоположными, погрешности складываются, т.е. 
3. Суммирование системной погрешности со случайной осуществляют с учетом корреляционных связей по тому же принципу, что и суммирование случайных погрешностей.
|
|
|
