 |
Понятия ссудного и учетного процента
|
|
|
|
ЛЕКЦИИ ПО ДИСЦИПЛИНЕ «ФИНАНСОВАЯ МАТЕМАТИКА»
Введение.
С развитием денежного обращения и используемого в расчетах математического аппарата совершенствовались и финансовые расчеты. Сейчас такие расчеты стали необходимыми для успешного проведения любой коммерческой деятельности. Вместе с современными методами анализа и моделирования финансовых ситуаций финансовые вычисления переросли в новое, все более влиятельное направление организации и управления предпринимательской деятельностью – финансовый менеджмент.
Ядром финансового менеджмента остается финансовая математика – изучающая определенные способы финансовых вычислений.
Финансовая математика – это область прикладной математики, предметом которой являются методы решения задач, необходимых при финансовых операциях.
Финансовая операция – это сделка между двумя или более участниками, в процессе которой осуществляется переход прав собственности на финансовые средства от одного участника сделки к другому (включая операции, связанные с использованием финансовых средств в качестве средства платежа).
Любые финансовые операции требуют учета трех групп параметров:
ü стоимостные характеристики (размеры платежей, кредитов, долговых обязательств);
ü временные данные (даты и сроки выплат, отсрочки платежей, продолжительность льготных периодов);
ü специфические элементы условий финансовых операций (ставки ссудного и учетного процента).
Все эти параметры равноправны, игнорирование какого-либо одного из них может привести к нежелательным финансовым последствиям для одной из участвующих сторон сделки.
Между различными видами параметров существуют функциональные зависимости. Изучение этих зависимостей и разработка на их основе методов решения финансовых задач – важнейшее направление деятельности специалистов в области финансовой математики.
|
|
|
Методы финансовой математики имеют сугубо практическое значение. Они применяются в финансовом менеджменте, оценочной деятельности, инвестиционном анализе, банковском деле, расчетах доходности операций на рынке ценных бумаг и валютном рынке, во внешнеэкономической деятельности.
В частности, они применяются:
ü в депозитарных операциях;
ü в кредитных операциях;
ü в операциях учета векселей;
ü при оценке стоимости любых активов или приносящего доход имущества, в т.ч. ценных бумаг;
ü при расчетах доходности вложений в финансовые инструменты;
ü при расчетах величины амортизационных отчислений и остаточной стоимости имущества.
Основные задачи финансовой математики:
1. Расчет конечных сумм денежных средств, находящихся во вкладах, займах, ценных бумагах путем начисления процентов;
2. Учет векселей и других ценных бумаг;
3. Установление взаимосвязи между отдельными параметрами сделки (финансовой операции) и определение неизвестных параметров, исходя из заданных значений известных параметров;
4. Определение эквивалентности параметров сделки с целью получения равной отдачи от затрат (финансовых вложений), произведенных различными способами;
5. Анализ последствий изменения условий финансовой операции;
6. Расчет обобщающих характеристик и отдельных параметров многократных регулярных поступлений или выплат денежных средств, рассматриваемых как финансовые потоки;
7. Разработка планов выполнения финансовых операций (т.е. финансовой стратегии организации);
8. Расчет показателей доходности финансовых операций.
Однако не следует считать, что с помощью простейших методов финансовых вычислений решаются все проблемы финансово-банковской и инвестиционной практики.
|
|
|
Методы и понятия финансовой математики обязательно используются в качестве исходных инструментов при создании более сложных методов количественного финансового анализа, которые изучают в других дисциплинах.
Лекция 1. ССУДНЫЙ И УЧЕТНЫЙ ПРОЦЕНТ.
Основные понятия финансовой математики
Важнейшей категорией финансовой математики является понятие процента, который в отличие от элементарной математики рассматривается не как сотая доля числа, а как доход, получаемый в результате предоставления кредитов и займов.
Большинство финансовых операций, в которых увеличение стоимости капитала происходит в результате предоставления его в долг и взимания процентной платы, требует проведения расчетов, основанных на методах финансовой математики.
В основе таких сделок лежат заранее оговоренные их субъектами правила получения дохода в виде процента от предоставления денежных средств в долг, т.е. части прибыли, полученной в результате оборота фондов денежных средств в процессе воспроизводства.
Таким образом, процент (процентный доход) выступает как причина изменения стоимости денежных средств во времени и именно поэтому рассматривается в качестве основной категории финансовый математики. Необходимо иметь ввиду, что процент в финансовой математике рассматривается не только как плата за пользование заемными средствами, а шире – как показатель доходности любого вложения капитала. (Причем это вложение капитала может и не состояться).
Процент или процентный доход (I) – это абсолютная величина дохода от предоставления денежных средств в долг на некоторый, заранее оговоренный срок, в любой его форме: выдача ссуды, продажа товара в кредит, учет векселя и т.д. (Или доход от любых видов финансовых вложений на определенный срок).
В любой сделке, связанной с финансовой операцией, всегда участвует две стороны, которые условно можно назвать кредитором и заемщиком. Если клиент берет в банке кредит, то в роли кредитора выступает банк, но если клиент наоборот, размещает свои денежные средства на банковском счете (депозите), то в таком случае он будет выступать в качестве кредитора для банка.
|
|
|
При заключении финансового или кредитного соглашения стороны (кредитор и заемщик) договариваются о размере процентной ставки.
Процентная ставка (i) – это относительная величина дохода за фиксированный отрезок времени, т.е. отношение дохода (процентных денег) к сумме долга за единицу времени. Процентная ставка измеряется в процентах и в виде десятичной или натуральной дроби, например 70% годовых, 3/12 годовых.
Помимо понятий «процент» и «процентная ставка» в финансовой математике фигурируют понятия: «первоначальная» (или текущая) и «наращенная» (или будущая) сумма денежных средств.
Первоначальная (или современная, имеющаяся в настоящее время) сумма (P или PV от англ. present value) – это исходная инвестируемая сумма.
Проценты согласно договоренности между кредитором и заемщиком регулярно выплачиваются по мере их начисления или присоединяются к основной сумме долга (т.е. происходит капитализация процентов).
Наращенная (или будущая) сумма (S или FV от англ. future value) – это первоначальная сумма с начисленными процентами (1).


Период (или срок) начисления – это весь промежуток времени, за который начисляются проценты.
Интервал начисления – это минимальный промежуток времени, по прошествии которого происходит начисление процентов. Например, первоначальная сумма может быть инвестирована на три года (период начисления), а проценты на нее будут начисляться каждый квартал, т.е. 3 месяца (интервал начисления).
В финансовой математике различают два способа начисления процентов:
ü декурсивный;
ü антисипативный.
При декурсивном способе проценты начисляются в конце каждого интервала начисления. Декурсивная ставка процента называется также ссудной ставкой (процентом) от англ. rate of interest).
При антисипативном (авансовом) способе проценты начисляются в начале каждого интервала начисления. Антисипативная ставка процента называется также учетной ставкой (процентом) от англ. discount rate).
В обоих способах начисления процентов процентные ставки могут быть в зависимости от базы для их начисления либо простыми – в течение всего периода начисления применяются к первоначальной сумме, либо сложными – в каждом интервале начисления применяются к текущей наращенной сумме.
|
|
|
Понятия ссудного и учетного процента
Ставка ссудного процента (i) может рассматриваться как стоимость услуги, оказываемой ссудодателем (кредитором) заемщику (клиенту), состоящей в предоставлении ему за плату некоторой суммы денежных средств на определенный срок, выраженная в процентах:
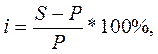

где: Р – сумма в настоящий момент времени;
S – наращенная сумма.
Наращенная сумма таким образом может быть рассчитана не только по формуле (1), но и по формуле (3):


Схема формирования наращенной суммы (будущей стоимости) представлена на рис. 1.
 | |||
 | |||
 настоящее будущее время
настоящее будущее время
Рис. 1. Схема формирования наращенной стоимости
Ссудный процент используется в кредитных и депозитарных операциях. Понятия «кредитный договор» и «депозитный вклад», а также условия заключения кредитных и депозитных договоров регламентируются Гражданским кодексом Российской Федерации.
По кредитному договору банк или иная кредитная организация (кредитор) обязуется предоставить денежные средства (кредит) заемщику в размере и на условиях, предусмотренных договором, а заемщик обязуется возвратить полученную денежную сумму и уплатить проценты на нее. (ГК РФ п. 1 ст. 819).
По договору банковского вклада (депозита) одна сторона (банк), принявшая поступившую от другой стороны (вкладчика) или поступившую для нее денежную сумму (вклад), обязуется возвратить сумму вклада и выплатить проценты на нее на условиях и в порядке, предусмотренных договором (ГК РФ п. 1 ст. 834).
|
|
|


