Главная | Обратная связь | Поможем написать вашу работу!

Максимизация ожидаемого дохода

Ответ

Строим матрицу выплат. Альтернативами или стратегиями магазина являются различные показатели пакетов с кефиром, которые ему, возможно, следует продать. Состояниями природы выступают величины спроса на аналогичное число пакетов. По условию, спрос на кефир может колебаться от 71 до 91 пакетов, поэтому магазину целесообразно продавать от 71 до 91 пакетов кефира.

Элементы платежной матрицы – это прибыль, которую получит компания в зависимости от выбранной альтернативы и спроса. Рассчитаем ее.

В итоге получим следующую платежную матрицу:

Продажа пакетов кефира	Спрос на кефир	Средняя ожидаемая прибыль


					455,65

	-16				131,25
Вероятность	0,2	0,25	0,45	0,1

Средняя ожидаемая прибыль продажи 91 пакета составит:

71*0,2+76*0,25+81*0,45+91*0,1= 131,25

Аналогичный расчет средней ожидаемой прибыли осуществляется для остальных объемов производства.

Исходя из критерия средней ожидаемой прибыли (5) следует остановиться на рекомендации продавать 76 пакетов

ЗАДАНИЕ 2. Для выпуска нового вида продукции рассматриваются 3 вариантов оборудования. Оборудование характеризуется следующими экономическими показателями:

Показатели	Оборудование

Постоянные издержки, млн. руб.		87,5	52,5
Средние переменные издержки, тыс. руб./шт.		36,5

Спрос на новую продукцию в течение месяца может принимать значения:

Спрос, тыс. шт.
Вероятность	0,3	0,4	0,3

Постройте дерево решений и определите наиболее подходящий тип оборудования, учитывая, что фирма стремится минимизировать ожидаемые затраты.

На основе данной таблицы затрат можно построить дерево решений (рис. 1).

Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение платежа.

Определим средние ожидаемые затраты (математическое ожидание):

Ø для оборудования 1

М(х) = 102000000+37000*850000*0,3= 9537000000 млн.руб.;

Ø для оборудования 2

М(х) = 87500000+36500*950000*0,4= 13957500000 млн.руб.;

Ø для оборудования 3

М(х) = 52500000+38000*1050000*0,3= 12022500000 млн.руб.;

Рис. 1. Построение дерева решений

Вывод. Так как по условию данной задачи фирма стремится минимизировать ожидаемые затраты, то наиболее целесообразно использовать оборудование 1, потому что средние ожидаемые затраты этого варианта минимальные из всех существующих и составляют 9537 млн.руб.

Задача

Имеются следующие данные о количестве и ценах угля, необходимого зимой для отопления дома (табл. 3.4). Вероятности зим: мягкой - 0,35; обычной - 0,5; холодной - 0,15.

Таблица 3.4

Зима	Количество угля, т	Средняя цена за 1 т в ф. ст.
Мягкая
Обычная		7,5
Холодная

Эти цены относятся к покупкам угля зимой. Летом цена угля 6 ф. ст. за 1 т, у вас есть место для хранения запаса угля до 6 т, заготавливаемого летом. Если потребуется зимой докупить недостающее количество угля, докупка будет по зимним ценам. Предполагается, что весь уголь, который сохранится до конца зимы, в лето пропадет.* Сколько угля летом покупать на зиму?

Решение. Построим платежную матрицу (табл. 3.5).

Таблица 3.5

Произведем расчет ожидаемой средней платы за уголь (табл. 3.6).

Таблица 3.6

Зима	Средняя ожидаемая плата
Мягкая	-(240,35+31,50,5+40*0,15)= -30,15
Обычная	-(300,35+300,5+38*0,15)= -31,2
Холодная	-(360,35+360,5+36*0,15)= -36

Как видим из табл. 3.6, наименьшая ожидаемая средняя плата приходится на случай мягкой зимы (30,15 ф. ст.). Соответственно если не учитывать степени риска, то представляется целесообразным летом закупить 4 т угля, а зимой, если потребуется, докупить уголь по более высоким зимним ценам.

Если продолжить исследование процесса принятия решения и аналогично задаче 3.5 вычислить средние квадратичные отклонения платы за уголь для мягкой, обычной и холодной зимы, то соответственно получим:

• для мягкой зимыsx = 5,357;

• для обычной зимы sx = 2,856;

• для холодной зимы sx = 0.

Минимальный риск, естественно, будет для холодной зимы, однако при этом ожидаемая средняя плата за уголь оказывается максимальной - 36 ф. ст.

Вывод. Мы склоняемся к варианту покупки угля для обычной зимы, так как согласно табл. 3.6 ожидаемая средняя плата за уголь по сравнению с вариантом для мягкой зимы возрастает на 3,5 %, а степень риска при этом оказывается почти в 2 раза меньшей (sx = 2,856 против 5,357).

Отношение среднего квадратичного отклонения к математическому ожиданию (средний риск на затрачиваемый 1 ф. ст.) для обычной зимы составляет = 0,0915 против аналогичного показателя для мягкой зимы, равного 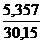= 0,1777, т.е. вновь различие почти в 2 раза.

Эти соотношения и позволяют нам рекомендовать покупку угля, ориентируясь не на мягкую, а на обычную зиму

Задача

Руководство некоторой компании решает, создавать ли для выпуска новой продукции крупное производство, малое предприятие или продать патент другой фирме. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка (табл. 3.1).

На основе данной таблицы выигрышей (потерь) можно построить дерево решений (рис. 3.1).

Рис. 3.1. Дерево решений без дополнительного обследования конъюнктуры рынка: ÿ - решение (решение принимает игрок): [*] - случай (решение "принимает" случай); // - отвергнутое решение

Таблица 3.1

Номер стратегии	Действия компании	Выигрыш, дол., при состоянии экономической среды*
благоприятном	неблагоприятном
	Строительство крупного предприятия (а₁)	200 000	-180 000
	Строительство малого предприятия (a₂)	100 000	-20 000
	Продажа патента (a₃)	10 000	-10 000

• Вероятность благоприятного и неблагоприятного состояний экономической среды равна 0,5.

Определим средний ожидаемый выигрыш (ОДО):

• для вершины 1 ОДО₁ = 0,5*200 000 + 0,5(-180 000) = 10 000 дол.;

• для вершины 2 ОДО₂ = 0,5*100 000 + 0,5(-20 000) = 40 000 дол.;

• для вершины 3 ОДО₃ = 10 000 дол.

Вывод. Наиболее целесообразно выбрать стратегию а₂, т.е. строить малое предприятие, а ветви (стратегии) а₁ и а₃ дерева решений можно отбросить. ОДО наилучшего решения равна 40 000 дол. Следует отметить, что наличие состояния с вероятностями 50 % неудачи и 50 % удачи на практике часто означает, что истинные вероятности игроку скорее всего неизвестны и он всего лишь принимает такую гипотезу (так называемое предположение «fifty - fifty» - пятьдесят на пятьдесят).

Усложним рассмотренную выше задачу.

Пусть перед тем, как принимать решение о строительстве, руководство компании должно определить, заказывать ли дополнительное исследование состояния рынка или нет, причем предоставляемая услуга обойдется компании в 10 000 дол. Руководство понимает, что дополнительное исследование по-прежнему не способно дать точной информации, но оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым значения вероятностей.

Относительно фирмы, которой можно заказать прогноз, известно, что она способна уточнить значения вероятностей благоприятного или неблагоприятного исхода. Возможности фирмы в виде условных вероятностей благоприятности и неблагоприятности рынка сбыта представлены в табл. 3.2. Например, когда фирма утверждает, что рынок благоприятный, то с вероятностью 0,78 этот прогноз оправдывается (с вероятностью 0,22 могут возникнуть неблагоприятные условия), прогноз о неблагоприятности рынка оправдывается с вероятностью 0,73.

Таблица 3.2

Прогноз фирмы	Фактически
Благоприятный	Неблагоприятный
Благоприятный	0,78	0,22
Неблагоприятный	0,27	0,73

Предположим, что фирма, которой заказали прогноз состояния рынка, утверждает:

• ситуация будет благоприятной с вероятностью 0,45;

• ситуация будет неблагоприятной с вероятностью 0,55.

На основании дополнительных сведений можно построить новое дерево решений (рис. 3.2), где развитие событий происходит от корня дерева к исходам, а расчет прибыли выполняется от конечных состояний к начальным.

Рис. 3.2. Дерево решений при дополнительном обследовании рынка (см. условные обозначения к рис. 3.1)

Анализируя дерево решений, можно сделать следующие выводы:

• необходимо проводить дополнительное исследование конъюнктуры рынка, поскольку это позволяет существенно уточнить принимаемое решение;

• если фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно строить большое предприятие (ожидаемая максимальная прибыль 116 400 дол.), если прогноз неблагоприятный - малое (ожидаемая максимальная прибыль 12 400 дол.).

Задача

АО «Фото и цвет» - небольшой производитель химических реактивов и оборудования, которые используются некоторыми фотостудиями при изготовлении 35-мм фильмов. Один из продуктов, который предлагает «Фото и цвет», - ВС-6. Президент АО продает в течение недели 11, 12 или 13 ящиков ВС-6. От продажи каждого ящика АО получает 35 дол. прибыли. Как и многие фотографические реактивы, ВС-6 имеет очень малый срок годности. Поэтому, если ящик не продан к концу недели, он должен быть уничтожен. Каждый ящик обходится предприятию в 56 дол. Вероятности продать 11, 12 и 13 ящиков в течение недели равны соответственно 0,45; 0,35; 0,2. Как вы советуете поступить? Как вы порекомендуете поступить, если бы «Фото и цвет» мог сделать ВС-6 с добавкой, значительно продлевающей срок его годности?

Решение. Матрицу игры с природой (здесь АО «Фото и цвет» - игрок с природой, а природа - торговая конъюнктура) строим по аналогии с рассмотренными выше задачами (табл. 3.7).

Таблица 3.7

* В скобках приведены вероятности спроса на ящики.

Расчет средней ожидаемой прибыли производится с использованием вероятностей состояний природы, как и в задачах 3.5 и 3.6.

Вывод. Наибольшая из средних ожидаемых прибылей (385 дол.) отвечает при заданных возможностях спроса производству 11 ящиков ВС-6.

Производство 11 ящиков в неделю и следует рекомендовать АО «Фото и цвет», ибо показатель риска - среднее квадратичное отклонение, как нетрудно убедиться, sx = 0 - минимален при максимальной средней ожидаемой прибыли.

Если срок службы химического реактива будет удлинен, то его производство даже при прежнем спросе можно увеличить, частично поставляя на склад для последующей реализации.

Задача

Для финансирования проекта бизнесмену нужно занять сроком на один год 15млн. руб. Банк может одолжить ему эти деньги под 15% годовых. В тоже время банк может вложить эту сумму в другой проект со 100%-ной гарантией возврата кредита, но под 9% годовых. Из прошлого опыта банкиру известно, что 4,1% таких клиентов ссуду не возвращают.

Что делать банку? Давать заем или нет? Постройте дерево решений и ответьте на вопросы.

Задача 1

Магазин «Молоко» продает в розницу молочные продукты. Директор магазина должен определить, сколько пакетов сметаны следует закупить у производителя для торговли в течение недели. Вероятности того, что спрос на сметану в течение недели будет 700,800,900 или 1000 упаковок, равны соответственно 0,2; 0,2; 0,5 и 0,1. Покупка одного пакета сметаны обходится магазину в 7 руб., а продается сметана по цене 11 руб. за пакет. Если сметана не продается в течение недели, она портится и магазин несет убытки.

Сколько пакетов сметаны желательно приобретать для продажи? Какова ожидаемая средняя прибыль магазина от этого решения?

Решение:

Спрос на сметану принимает значения 700, 800, 900, 1000, т.е. возможны 4 рыночные ситуации. С другой стороны, т.к. магазин может купить от 700 до 1000 упаковок сметаны, то у него есть 4 возможных курса действия. Строим матрицу выплат.

На пересечении строк и столбцов матрицы – ожидаемая прибыль магазина. Заполним таблицу. Если магазин закупит 700 упаковок сметаны и продаст 700, то прибыль магазина составит:

П = TR – TC = P∙Q – ATC∙Q = 11∙700 – 7∙700 = 2800 руб.

Если магазин закупит 700 упаковок, то каким бы ни был спрос, более 700 упаковок продать нельзя. Потому прибыль в первой строке таблицы будет равна 2800.

Закупка 800 упаковок сметаны обойдется магазину в 7∙800=5600 руб., а от продажи 700 упаковок выручка составит TR = 11∙700 = 7700 руб. Суммарная прибыль П = 7700 – 5600 = 2100 руб.

Рассуждая подобным образом, заполним таблицу выплат.

Закупаемое количество упаковок сметаны, шт.	Ситуация на рынке (объем спроса)	Математическое ожидание
700 (0,2)	800 (0,2)	900 (0,5)	1000 (0,1)

Определим среднюю ожидаемую прибыль для каждого курса действий:

1. при покупке 700 упаковок 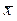= 2800.

2. при покупке 800 упаковок 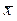= 2100∙0,2 + 3200∙0,8 = 2980.

3. при покупке 900 упаковок = 1400∙0,2 + 2500∙0,2 + 3600∙0,6 = 2940.

4. при покупке 1000 упаковок = 700∙0,2 + 1800∙0,2 + 2900∙0,5 + 400∙0,1 = 2350.

Наибольшую ожидаемую прибыль приносит покупка 800 упаковок сметаны. Этот курс действий и будет выбран. Средняя ожидаемая прибыль при выборе этого варианта составит 2980 руб.

Ответ: 800 упаковок; 2980 руб.

Задача 4

Автомобильный завод получает реле поворота от двух поставщиков: А и В. Качество этих изделий характеризуется следующими данными:

Процент брака	Вероятность для поставщика
А	В
	0,7	0,4
	0,1	0,3
	0,09	0,15
	0,07	0,1
	0,04	0,05

Полные затраты, связанные с ремонтом одного бракованного реле, составляют 5 руб.

Реле поступают партиями по 20000 шт. Поскольку качество изделий у поставщика В хуже, он уступает всю партию на 500 руб. дешевле.

Постройте дерево решений. Какого поставщика следует выбрать?

Решение:

Строим дерево решений.

Выплаты для каждой ветки – это потери автомобильного завода, связанные с ремонтом бракованных реле. Расчет следующий.

Так как партия поставки 20000 шт., в партии 1% брака, то количество бракованных реле в партии 200 шт., затраты на ремонт составляют 200∙5 = 1000 руб.

Аналогично расчеты проводятся для остальных значений брака (2%, 3%, 4%, 5%). Так как затраты на ремонт – это потери предприятия, то ставится знак минус «-».

Для заполнения кружков графика находимы соответствующие значения математического ожидания потерь.

М(х_А) = (-1000)∙0,7 + (-2000)∙0,1 + (-3000)∙0,09 + (-4000)∙0,07

+ (-5000)∙0,04 = -1650 руб.

М(х_В) = (-1000)∙0,4 + (-2000)∙0,3 + (-3000)∙0,15 + (-4000)∙0,1 + (-5000)∙0,05 = -2100 руб.

Так как поставщик В предлагает скидку, то средние ожидаемые потери по поставщику В снижаются на 500 руб. и составляют -2100+500 = -1600.

Средние ожидаемые затраты на ремонт бракованных реле, полученных от поставщика В (1600) меньше, чем потери по поставщику А (1650). Значит, оптимальным является решение о выборе поставщика В.

Задача

Главный инженер предприятия решает, строить или не строить новую производственную линию, использующую более современную технологию. Если новое оборудование заработает, компания будет получать прибыль $ 200 000. Если не заработает, то компания получит убыток $ 150 000. Главный инженер считает, что шансы на успех нового процесса – 60 %.

Другое решение – проводить дополнительное исследование и тогда решать пускать или не пускать новую линию. Такое исследование требует затрат $ 10 000. Главный инженер считает, что шанс того, что исследование даст благоприятный результат 50%. Если оно успешно, то вероятность того, что оборудование будет работать 0,9. Если нет, то только 20% составляет вероятность того, что оборудование будет работать. Перед лицом главного инженера дилемма.

Должен ли он проводить исследование и затем принимать решение? Какое решение следует принять главному инженеру?

Решение:

Строим дерево решений.

где БР – благоприятный рынок;

НР – неблагоприятный рынок.

Рассчитываем математическое ожидание.

М(х₁) = 200000∙0,6 + (-150000)∙0,4 = 60000 долл.

М(х₂) = 200000∙0,9 + (-150000)∙0,1 = 165000 долл.

М(х₃) = 200000∙0,2 + (-150000)∙0,8 = -80000 долл.

М(х₄) = 165000∙0,5 + 0∙0,4 = 82500 долл.

Исследования рынка позволяет уточнить ожидаемые оценки и получить более высокую ожидаемую прибыль – 72500 (82500 - 10000) долл.

Вывод. Дополнительное исследование следует проводить. Если результаты исследования положительные, то следует строить новую производственную линию. Если результаты исследования неблагоприятны, то ничего не следует строить.

Задача

Небольшая фирма производит косметическую продукцию для подростков. В течение месяца реализуется 10+К, 15+К или 20+К упаковок товара. От продажи каждой упаковки фирма получает (200+10*К) руб. прибыли. Косметика имеет малый срок годности, поэтому, если упаковка не продана в месячный срок, она должна быть уничтожена. Поскольку производство одной упаковки обходится в (100+10*К) руб., потери фирмы составляют (100+10*К) руб., если упаковка не продана к концу месяца. Вероятности продать 10+К,15+К или 20+К упаковок за месяц составляют соответственно 0,25; 0,4; 0,35.

Постройте матрицу выплат. Сколько упаковок косметики следует производить фирме ежемесячно? Какова ожидаемая стоимостная ценность этого решения? Сколько упаковок можно было бы производить при значительном продлении срока хранения косметической продукции?

Решение

В данной задаче альтернативами является количество упаковок косметики, которое следует производить фирме. Состояниями среды выступают величины спроса на аналогичное число упаковок косметики. По условию, спрос на косметику может колебаться от 24 до 36 упаковок, поэтому компании целесообразно производить от 24 до 36 упаковок.

Элементы матрицы выплат – это прибыль, которую получит фирма в зависимости от выбранной альтернативы и спроса. Ее расчет.

Если фирма производит 24 упаковки и спрос на них равен 24, тогда прибыль в данном случае равна 24*140=3360. Если фирма производит 24 упаковки спрос на них равен 29, тогда прибыль в данном случае равна 24*140=3360 рублей. Если фирма производит 24 упаковки спрос на них равен 34, тогда прибыль в данном случае равна 24*140=3360.

Если фирма производит 29 упаковок косметики и спрос на них равен 24, тогда прибыль от продажи 24 упаковок равна 24*140=3360 рублей, а убытки от непроданных 5 упаковок равны 940*5=4700 рублей, тогда прибыль в данном случае равна 3360-4700=-1340 рублей (т.е. убытки 1340 рублей).Если фирма производит 29 упаковок косметики и спрос на них равен 34, тогда прибыль в данном случае равна 29*140=4060 рублей.

Если фирма производит 34 упаковки косметики и спрос на них равен 24, тогда прибыль от продажи 24 упаковок равна 24*140=3360 рублей, а прибыль в данном случае равна 3360-9400=-6040 рублей (т.е. убытки 6040 рублей). Если фирма производит 34 упаковки косметики и спрос на них равен 29, тогда прибыль от продажи 29 упаковок равна 29*140=4060, а убытки от непроданных 5 упаковок равны 940*5=4700 рублей, тогда прибыль в данном случае равна 4060-4700=-640 рублей (т.е. убытки 640 рублей). Если фирма производит 34 упаковки косметики и спрос на них равен 34, тогда прибыль в данном случае равна 34*140=4760 рублей.

В итоге получится следующая матрица выплат:

Объем производства	Спрос на косметику	X	сигма
24(0.4)	29(0.35)	34(0.25)

	-1340
	-6040	-640		-1450

Средняя ожидаемая прибыль продажи 24 упаковок косметики составит:

X24=3360*0.4+3360*0.35+3360*0.25=3360(руб.)

X29=-1340*0.4+4060*0.35+4060*0.25=-1900(руб.)

X34=-6040*0.4+640*0.35+4760*0.25=-1450(руб.)

Дисперсии равны:

D24=(3360-3360)2*0.4+(3360-3360)2*0.35+(3360-3360)2*0.25

D29=(1900+1340)2*0.4+(1900-4060)2*0.35+(1900-4060)2*0.25=6998400

D34=(-1450+6040)2*0.4+(-1450+640)2*0.35+(-1450-4760)2*0.25=18297900

Среднеквадратические отклонения равны:

сигма24=корень(0)

сигма29=корень(6998400)

сигма34=корень(18297900)

Исходя из критерия средней ожидаемой прибыли, К=3360рублей при производстве 24 упаковок косметики, т.е. исходя из критерия максимума средне ожидаемой прибыли, необходимо производить 24 упаковки косметики, при этом прибыль составит 3360 рублей.

Исходя из критерия ожидаемого риска, К=2645 рублей при производстве 29 упаковок косметики, т.е. исходя из критерия максимума средне ожидаемой прибыли, необходимо производить 29 упаковки косметики, при этом прибыль составит 1900 рублей.

Если продолжить срок хранения косметической продукции, то изменятся элементы матрицы выплат. Ее расчет.

Если фирма производит 34 упаковки косметики и спрос на них равен 24, тогда прибыль в данном случае равна 24*140=3360 рублей. Если фирма производит 24 упаковки косметики и спрос на них равен 29, тогда прибыль в данном случае равна 24*140=3360 рублей. Если фирма производит 24 упаковки косметики и спрос на них равен 34, тогда прибыль в данном случае равна 24*140=3360 рублей.

Если фирма производит 29 упаковки косметики и спрос на них равен 24, тогда прибыль от продажи 24 упаковок равна 24*140=3360 рублей. Если фирма производит 29 упаковки косметики и спрос на них равен 29, тогда прибыль в данном случае равна 29*140=3360 рублей. Если фирма производит 29 упаковки косметики и спрос на них равен 34, тогда прибыль в данном случае равна 34*140=4760 рублей.

В итоге получается следующая матрица выплат:

Объем производства	Спрос на косметику	X	сигма
24(0.4)	29(0.35)	34(0.25)

Средняя ожидаемая прибыль продажи 24 упаковок косметики составит:

X24=3360*0.4+3360*0.35+3360*0.25=3360(руб.)

Средняя ожидаемая прибыль продажи 29 упаковок косметики составит:

X29=3360*0.4+4060*0.35+4060*0.25=3780(руб.)

Средняя ожидаемая прибыль продажи 34 упаковок косметики составит:

X34=3360*0.4+4060*0.35+4760*0.25=3955(руб.)

Дисперсии равны:

D24=(3360-3360)2*0.4+(3360-3360)2*0.35+(3360-3360)2*0.25

D29=(3780-3360)2*0.4+(3780-4060)2*0.35+(3780-4060)2*0.25=117600

D34=(3955-3360)2*0.4+(3955-4060)2*0.35+(3955-4760)2*0.25=307475

Среднеквадратические отклонения равны:

сигма24=корень(0)

сигма29=корень(6998400)

сигма34=корень(18297900)

Исходя из критерия средней ожидаемой прибыли:

Т.о. К=3955 рублей при производстве 34 упаковок косметики, т.е. исходя из критерия максимума средне ожидаемой прибыли, необходимо производить 34 упаковки косметики, при этом прибыль составит 3955 рублей.

Исходя из критерия ожидаемого риска, К=343 рублей при производстве 29 упаковок косметики, т.е. исходя из критерия максимума средне ожидаемой прибыли, необходимо производить 29 упаковки косметики, при этом средне ожидаемая прибыль составит 3780 рублей, риск – 343 рубля.

Задача

Предприниматель собирается построить ночную дискотеку неподалеку от университета. По одному из допустимых проектов предприниматель может в дневное время открыть в здании дискотеки столовую для студентов и преподавателей. Другой вариант не связан с дневным обслуживанием клиентов. И в том и в другом случае, его шансы на успех будут 0,6 (провал – 0,4). Представленные бизнес-планы показывают, что план, связанный со столовой, может принести доход в 415000 тыс. руб.. Без открытия столовой бизнесмен может заработать 340000 тыс. руб. Потери в случае открытия дискотеки со столовой составят 160000 тыс. руб., а без столовой – 110000 тыс. руб.

Постройте дерево решений. Определите наиболее эффективную альтернативу.

Решение:

Номер стратегии	Действия компании	Выигрыш, руб., при состоянии экономической среды
благоприятном (Р=0,6)	неблагоприятном (Р=0,4)
	Столовая (а1)		-160000
	Дневное обслуживание клиентов (а2)		-110000

На основе данной таблицы выигрышей (потерь) можно построить дерево решений.

Определим средний ожидаемый выигрыш (математическое ожидание):

Ø для столовой

М(х) = 0,6*415 000 + 0,4(-160 000) = 185000 руб.;

Ø для маленького предприятия

М(х) = 0,6* 340 000 + 0,4(-110 000) = 160000 руб.;

Вывод. Наиболее целесообразно открыть столовую. Средний ожидаемый выигрыш наилучшего решения равен 185000 руб.

Издатель обратился в отдел маркетинга, чтобы выяснить предполагаемый спрос на книгу, исследования одела маркетинга показали- данные в таблице.

Спрос на книгу в ближайший год, кол. экз.
Вероятность	0,1	0,2	0,3	0,2	0,2

Смета расходов и размер прибыли составляют 90 грн. Если книга не продается, убытки составляют 30 грн. За штуку. Если издатель не удовлетворяет спрос, убытки по неудовлетворенному спросу составят 10 грн.(для поддержания репутации фирмы и будущего спроса. Используя каждое из правил, определите, сколько книг должно быть издано в расчете на год.

Решение

Таблица 1. Доход (прибыль) в год, грн.

Спрос	Кол-во книг	max/max	max/min

					15000(max)
					15000(max)


				45000(max)

1.1)90*200=18000

1.2)(90*200)-(100*10)=18000-1000=17000

1.3)(90*200)-(200*10)=18000-2000=16000

1.4)(90*200)-(250*10)=18000-2500=15500

1.5)(90*200)-(300*10)=18000-3000=15000

2.1)(90*200)-(100*30)=18000-3000=15000

2.2)90*300=27000

2.3)(90*300)-(100*10)=27000-1000=26000

2.4)(90*300)-(150*10)=27000-1500=25500

2.5)(90*300)-(200*10)=27000-2000=25000

3.1)(90*200)-(200*30)=18000-6000=12000

3.2)(90*300)-(100*30)=27000-3000=24000

3.3)90*400=36000

3.4)(90*400)-(50*10)=36000-500=35500

3.5)(90*400)-(100*10)=36000-1000=35000

4.1)(200*90)-(250*30)=18000-7500=10500

4.2)(300*90)-(150*30)=27000-4500=22500

4.3)(400*90)-(50*30)=36000-1500=34500

4.4)450*90=40500

4.5)(450*90)-(50*10)=40500-500=40000

5.1)(200*90)-(300*30)=18000-9000=9000

5.2)(300*90)-(200*30)=27000-6000=21000

5.3)(400*90)-(100*30)=36000-3000=33000

5.4)(450*90)-(50*30)=36000-3000=39000

5.5)500*90=45000

Правило максимакса – максимизация максимума доходов.Согласно критерию max/max необходимо издавать 500 ед. книг, что бы обеспечить максимальную прибыль.

Правило миксимин-максимизация минимальных результатов.

Критерий Севиджа (min/ max)

спрос	Кол-во книг
		min/ max
			9000(min)

Согласно критерию min/ max минимальная величина максимальных потерь возникает в результате издательства 200 ед. книг в год.

Критерий Гурвица

Спрос	Доход	Вес	Всего
н	в	0,4	0,6




				30600(max)

В данном примере критерий Гурвица свидетельствует в пользу решения о издательстве 500 ед. книг, максимальная сумма составила 30600 тыс.руб.

Максимизация ожидаемого дохода

Максимизирует ожидаемый доход для решений:

М(х)=∑(вероятность × доход)(суммируем для всех исходов рассматриваемого решения)

Спрос	Кол-во книг	Вер-ть

			0,1
			0,2
			0,3
			0,2
			0,2
М(х)

1)(0,1*18000)+(17000*0,2)+(16000*0,3)+(15500*0,2)+(15000*0,2)=16100

2)(0,1*15000)+(0,2*27000)+(26000*0,3)+(15500*0,2)+(25000*0,2)=22800

3)(12000*0,1)+(24000*0,2)+(36000*0,3)+(35500*0,2)+(35000*0,2)=30900

4)(10500*0,1)+(22500*0,2)+(34500*0,3)+(40500*0,2)+(40000*0,2)=32000

5)(9000*0,1)+(21000*0,2)+(33000*0,3)+(39000*0,2)+(45000*0,2)=31800

Итак, максимальное значение ожидаемого дохода 32000 тыс.руб в год, следовательно, используя критерий максимизации ожидаемого дохода, издатель должен издавать 450 ед. книг.

Воспользуйтесь поиском по сайту: