Индивидуальное задание студента

ЛАБОРАТОРНАЯ РАБОТА № 1

По дисциплине «Имитационное моделирование»

Модели межотраслевого баланса

Цель занятия:

- ознакомиться с содержанием таблицы «Затраты – выпуск»;

- освоить методы построения балансовых моделей;

- освоить методы решения балансовых моделей с помощью

программы MS Excel.

Краткие сведения из теории

Балансовые модели применяются для изучения сложных структур, как на отраслевом уровне, так и на уровне отдельных предприятий. Исходной базой для анализа балансовых моделей является таблица «Затраты – выпуск», которая в простейшем виде имеет вид таблицы 1.

 

Пример 1. Исходя из сложившейся структуры производства (табл.1), определите:

а) матрицу прямых затрат, матрицу полных затрат и матрицу косвенных затрат;

б) сбалансированные уровни производства валовой продукции на следующий период, если план по конечной продукции принят в промышленности в 100 ед., в строительство в 30 ед., в сельском хозяйстве – в 20 ед.

в) матрицу межотраслевых поставок продукции для планового года;

г) сведите в таблицу той же формы всю полученную информацию для планового года.

 

Таблица 1

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

Решение.

1. Определим матрицу прямых затрат

2. Определим матрицу

определитель этой матрицы

Матрица S невырожденная, т.к.

3. Матрицу полных затрат 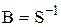найдем методом присоединенной матрицы.

Вычислим алгебраические дополнения матрицы S:

 

 

 

 

Присоединенная матрица

 

Матрица полных затрат

 

 

4. Матрицу косвенных затрат С определим по формуле

 

5. Сбалансированный уровень производства валовой продукции рассчитаем по основному уравнению:

 

 

6. Матрицу межотраслевых поставок продукции для планового года определим по формуле: , i=1,2,3

Таблица 3.3

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность	72,7	12,3	5,3
	Строительство
	Сельское хоз-во	22,2		12,2
	Всего		12,3	17,5

 

Рассмотрим ещё пример построения балансовой модели при задании матрицы коэффициентов прямых затрат (табл.2). Необходимо найти коэффициенты полных материальных затрат B, валовую продукцию X_j и чистую Z_j продукцию.

Таблица 2 – Исходные данные для расчета

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,3	0,1	0,4
Отрасль 2	0,2	0,5
Отрасль 3	0,3	0,1	0,2
Условно чистая продукция, Zj
Валовая продукция, Xj

Последовательность расчета включает следующие этапы.

1. Представим исходные данные в матричной форме:

- матрица коэффициентов прямых затрат А

A = ;

- конечная продукция Y = .

2. Найдем матрицу (Е – А), где Е – единичная матрица.

(Е – А) = - = .

3. Вычислим определитель матрицы (Е – А):

= = 0,196.

4. Найдем алгебраические дополнения A_d матрицы:

A_d = .

5. Вычислим матрицу коэффициентов полных затрат:

B = (E – A)^-1 = A_d/ = .

6. Определим величины валовой продукции:

X = B Y = .

7. Определим величины межотраслевых потоков:

x_ij = x_ij X_j,

8. Рассчитаем величину чистой продукции:

Z_j = X_j - .

Результаты расчетов сведем в таблицу 3.

Таблица 3 – Результаты расчетов

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	232,6	51,0	291,8		775,3
Отрасль 2	155,1	255,0			510,1
Отрасль 3	232,6	151,0	145,9		729,6
Условно чистая продукция, Zj	155,0	153,1	291,9	Итого: 600
Валовая продукция, Xj	775,3	510,1	729,6		Итого:2015

 

Покажем последовательность расчетов межотраслевого баланса с использованием пакета MS Excel.

Исходя из сложившейся структуры производства (табл.4), определить:

- матрицы прямых затрат, полных и косвенных затрат;

- матрицу межотраслевых поставок X_ij;

- общие (валовые) объемы выпускаемой продукции, если известны результаты деятельности текущего периода.

Таблица 4 – Исходные данные для расчета

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1
Отрасль 2
Отрасль 3
Zj
Xj

 

1. Представим исходные данные в матричной форме:

- матрица коэффициентов прямых затрат a_ij = x_ij / X_j:

 

A = ; - матрица конечной продукции: Y = .

 

Вычислим матрицу (Е – А), введя формулы в ячейки B8:D10. Получим результат:

(Е – А) = .

 

2. Введем исходные данные в таблицу Excel (рис.1).

 

 

	A	B	C	D	E	F
		Отрасль1	Отрасль2	Отрасль3	Yj	Xj
	Отрасль1	0,36	0,41	0,10		=МУМНОЖ (B12:D14;E2:E4)
	Отрасль2
	Отрасль3	0,11		0,23
	Zj	=B6 – СУММ (B16:B18)	=C6 – СУММ (C16:C18)	=D6 – СУММ (D16:D18)
	Xj	=F2	=F3	=F4
		Матрица E - A
		=1-B2	=0-C2	=0-D2
	E - A	=0-B3	=1-C3	=0-D3
		=0-B4	=0-C4	=1-D4
		Матрица полных затрат B
		=МОБР(B8:D10)
	B
		Матрица межотраслевых поставок
		=B2*B6	=C2*C6	=D2*D6
	Xij	=B3*B6	=C3*C6	=D3*D6
		=B4*B6	=C4*C6	=D4*D6

 

Рис. 1 – Исходные данные

 

 

3. Рассчитаем матрицу полных затрат B = (E – A)^-1 с помощью функции МОБР:

- для этого выделим область матрицы – ячейки (B12:D14);

- вызовем функцию МОБР и укажем диапазон исходных данных (B8:D10);

- одновременным нажатием клавиш Shift + Ctrl + Enter

получим матрицу B = .

 

4. Определим величины валовой продукции X = B Y, используя функцию МУМНОЖ:

- выделим ячейки (F2:F4);

- вызовем функцию МУМНОЖ и для неё укажем диапазон исходных данных: массив 1 – (B12:D14), массив 2 – (E2:E4);

- одновременным нажатием клавиш Shift + Ctrl + Enter получаем искомый результат: X = .

 

5. Определим величины межотраслевых потоков x_ij = a_ij X_j:

- в ячейки B6,C6,D6 запишем значения клеток F2,F3,F4 соответственно;

- в ячейки (B17:D19) запишем формулы вычисления межотраслевых поставок, например, в ячейке B16 будет запись =B2*B6. В результате получим матрицу: (x_ij) = .

 

6. Рассчитаем величину чистой продукции Z_j = X_j - , введя в ячейки (B5:D5) соответствующие формулы, например, в ячейке B5 запишем

=B6–СУММ(B16:B18), в ячейке C5 - =C6–СУММ(C16:C18) и т.д.

Получим значения величин чистой продукции каждой отрасли:

Z = .

Результаты расчетов представлены в виде таблицы на рис.2.

 

	отрасль1	отрасль2	отрасль3	Y	Xj
отрасль1	0,36	0,41	0,1		169,7702
отрасль2
отрасль3	0,11		0,23		47,62951
Zj	89,97823	17,11	31,91177
Xj	169,7702		47,62951
	Матрица	Е - А
	0,64	-0,41	-0,1
Е - А
	-0,11		0,77
	Матрица	B
	1,598174	0,655251	0,207555
B
	0,228311	0,093607	1,328352
	Матрица	(xij)
	61,11729	11,89	4,762951
(xij)
	18,67473		10,95479

 

Рис.2 Результаты расчета

На рис.2 приведены сбалансированные результаты расчета трехотраслевой модели. Таким образом, получили данные, которые могут быть использованы для планирования выпуска продукции следующего года.

 

Индивидуальное задание студента

Исходя из сложившейся структуры производства (таблица исходных данных), определите:

-матрицу прямых затрат, матрицу полных затрат и матрицу косвенных затрат;

- матрицу межотраслевых поставок продукции;

- провести расчеты с использованием пакета MS Excel;

- данные расчетов оформить в виде отчета в формате А4.

 

Вариант 1

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

Вариант 2

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

Вариант 3

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

 

Вариант 4

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

Вариант 5

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

Вариант 6

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

Вариант 7

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

Вариант 8

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

 

Вариант 9

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

 

Вариант 10

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

Вариант 11

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,2	0,1	0,4
Отрасль 2	0,25	0,4	0,2
Отрасль 3	0,5	0,125	0,2
Zj
Xj

Вариант 12

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,2	0,1	0,1
Отрасль 2	0,1	0,2	0,2
Отрасль 3	0,5	0,05	0,3
Zj
Xj

 

Вариант 13

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,2	0,5	0,1
Отрасль 2	0,2	0,2	0,2
Отрасль 3	0,05	0,1	0,1
ZJ
Xj

 

Вариант 14

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,1	0,3	0,2
Отрасль 2	0,1	0,2	0,4
Отрасль 3	0,3	0,1	0,1
Zj
Xj

 

Вариант 15

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,2	0,1	0,1
Отрасль 2	0,4	0,2	0,3
Отрасль 3	0,3	0,2	0,1
Zj
Xj

 

Вариант 16

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,5	0,2
Отрасль 2	0,2		0,1
Отрасль 3		0,1	0,2
Zj
Xj

Вариант 17

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,1	0,2	0,15
Отрасль 2	0,05	0,5	0,05
Отрасль 3	0,3	0,2	0,25
Zj
Xj

 

Вариант 18

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1		0,2	0,3
Отрасль 2	0,4		0,1
Отрасль 3	0,5	0,2
Zj
Xj

 

Вариант 19

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1		0,1	0,4
Отрасль 2	0,2		0,1
Отрасль 3	0,3	0,1
Zj
Xj

Вариант 20

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1		0,1	0,2
Отрасль 2	0,3		0,4
Отрасль 3	0,1	0,2
Zj
Xj

 

Вариант 21

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,2	0,2	0,1
Отрасль 2	0,5	0,3	0,2
Отрасль 3	0,2	0,2	0,4
Zj
Xj

 

Вариант 22

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1		0,1	0,2
Отрасль 2	0,3		0,4
Отрасль 3	0,1	0,2
Zj
Xj

Вариант 23

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,2	0,2	0,1
Отрасль 2	0,5	0,3	0,2
Отрасль 3	0,2	0,2	0,4
Zj
Xj

 

Вариант 24

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1		0,1	0,2
Отрасль 2	0,3		0,4
Отрасль 3	0,1	0,2
Zj
Xj

 

Вариант 25

Производящая Отрасль	Затраты потребляющей отрасли А	Конечная Продукция Yj	Валовая продукция Xj
Отрасль 1	Отрасль 2	Отрасль 3
Отрасль 1	0,1	0,2	0,15
Отрасль 2	0,05	0,5	0,05
Отрасль 3	0,3	0,2	0,25
Zj
Xj

Вариант 26

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

Вариант 27

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

Вариант 28

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

 

Вариант 29

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

Вариант 30

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

Вариант 31

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

Вариант 32

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

Вариант 33

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

 

Вариант 34

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего

 

 

Вариант 35

№№	Отрасли производства	Потребление	Конечная продукция	Валовая продукция
	Промышленность
	Строительство
	Сельское хоз-во
	Всего		Поделиться: Воспользуйтесь поиском по сайту: ©2015 - 2025 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...