 |
Вычисление площадей плоских фигур
|
|
|
|
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пусть функция 
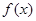 определена на отрезке
определена на отрезке 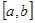 . Разделим отрезок [ a,b ] на n произвольных частей точками a=x0 <x1 <x2 ……<xn-1<xn =b, выберем на каждом элементарном отрезке [ xk-1,xk ] произвольную точку xk и найдём длину каждого такого отрезка: D xk=xk-xk-1. Тогда интегральной суммой для функции f(x) на отрезке [ a,b ] называется сумма вида
. Разделим отрезок [ a,b ] на n произвольных частей точками a=x0 <x1 <x2 ……<xn-1<xn =b, выберем на каждом элементарном отрезке [ xk-1,xk ] произвольную точку xk и найдём длину каждого такого отрезка: D xk=xk-xk-1. Тогда интегральной суммой для функции f(x) на отрезке [ a,b ] называется сумма вида
|
Эта сумма имеет конечный предел J, если для любого, сколь угодно малого положительного числа e>0 найдётся такое число d>0, что как только длина наибольшего из элементарных отрезков станет меньше чем d (то есть выполнится неравенство max D xk <d) неравенство |s-J|<e будет выполняться при любом выборе точек xk внутри элементарных отрезков[ xk-1,xk ].
Определённым интегралом от функции f(x) на отрезке [ a,b ] (или в пределах от a до b) называется число J, являющееся пределом интегральной суммы при условии, что длина наибольшего из элементарных отрезков (max D xk) стремится к нулю:
|
Теорема. Если функция f(x) непрерывна (кусочно-непрерывна) на [ a,b ], то предел интегральной суммы при max D xk ®0 существует и не зависит ни от способа разбиения [ a,b ] на элементарные отрезки, ни от выбора точек xk.
Числа a и b называются нижним и верхним пределами интегрирования.
Основные свойства определённого интеграла:
b а
1. ò f(x) dx = -ò f(x) dx
a b
a
2. ò f(x) dx=0
a
b c b
3. ò f(x) dx= ò f(x) dx + ò f(x) dx
a a c
b b b
4. ò [f1(x)±f2(x)]dx= ò f1(x) dx ± ò f2(x) dx
a a a
b b
5. ò C f(x) dx=Cò f(x) dx
a a
6. Оценка определённого интеграла: если m£f(x)£M на [ a,b ], то
b
m(b-a)<ò f(x) dx<M(b-a).
a
Приемы вычисления определённого интеграла
1. Формула Ньютона-Лейбница:
|
|
|
b
òf(x)dx = F(b) - F(a), где F(x) любая первообразная для f(x), т.е. F¢(x)=f(x).
a
2. Интегрирование по частям
b b b
òUdV = UV½ - òVdU, где U=U(x) и U=U(x) - дифференцируемые на отрезке
a a a
[a,b] функции.
3. Замена переменной:
b b
òf(x)dx = òf[j(t)]j¢(t)dt, где x=j(t) - функция, непрерывная вместе со своей
a a
производной на отрезке a£t£b, a=j(а), b=j(b), f[j(t)] - непрерывная на [a,b].
a
4. а) Если f(x) - нечетная функция, т.е. f(-x) = -f(x), то òf(x) dx=0
-a
б) Если f(x) - четная функция, т.е. f(-x)=f(x), то  f(x)dx = 2
f(x)dx = 2 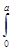 f(x) dx
f(x) dx
Примеры:
________
1. Вычислить 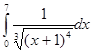 .
.
Используем табличный неопределенный интеграл вида òUndU для нахождения первообразной функции и применим формулу Ньютона-Лейбница.. В подынтегральном выражении степенная функция умножается на дифференциал от её основания.
Найдём дифференциал от основания данной степенной функции - d(x+1)=dx, тогда имеем:
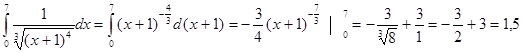
2. Вычислить  .
.
Для вычисления этого интеграла используем табличный вида ò 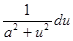 .
.
Так как x8=(x4)2 и d(x4) =4x3dx, то
 =
= 

3. Вычислить 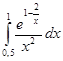
В этом примере используем табличный интеграл вида òeU dU. Найдём дифференциал от показателя степени d(1-2/x)=2/x2 dx, тогда можно записать
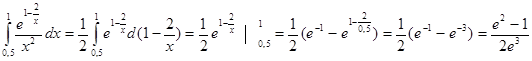
4. Вычислить 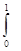 xe-x dx
xe-x dx
Воспользуемся методом интегрирования по частям. Положим U=x, dU=e-x dx,
Тогда dU=dx, U=-e-x.
1 1 1 1
òxe-x dx=-xe-x ½+òe-x dx= - e-1 - e-x½=-2e-1+1=(e-2)/e
0 0 0 0
5. Вычислить 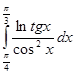
Интегрируем по частям. Положим U= ln tgx, dU=  dx, тогда
dx, тогда
dU= 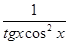 , U=òdU=ò
, U=òdU=ò  dx=tgx
dx=tgx
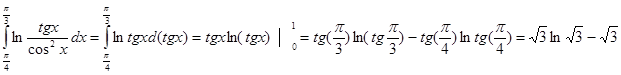
6. Вычислить  .
.
Введём переменную 1+lnx=t, lnx=t-1, тогда dx/x =dt. Находим новые пределы интегрирования tн=1+ln1=1, tв=1+ln e3 =1+3ln e=1+3=4, следовательно,
e3
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
Площадь всякой плоской фигуры в прямоугольной системе координат может быть представлена в виде суммы или разности площадей криволинейных трапеций, прилегающих к оси 0x или 0y.
1. Площадь плоской фигуры, ограниченной непрерывной кривой, уравнение которой имеет вид y=f(x), осью Ox и двумя прямыми x=a и x=b, где a£x£b, f(x)³0, находится по формуле:
|
|
|
 |
b У
 S=òf(x) dx y=f(x)
S=òf(x) dx y=f(x)

 a
a
S
 О
О
a b Х
2. В том случае, когда криволинейная трапеция, ограниченная кривой y=f(x), осью Ох и прямыми х=a и х=b, лежит под осью Ох, площадь находится по формуле
b y


 S=ò½f(x)½ dx a b x
S=ò½f(x)½ dx a b x
a О
S
 |
3. Если криволинейная трапеция прилегает к оси Оу так, что c£y£d, x=j(x), то площадь плоской фигуры находится по формуле
 |
d y
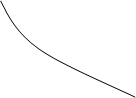 S=òj(y) dy х=j(y)
S=òj(y) dy х=j(y)
 c d
c d
S

 c x
c x
4. 
 Если фигура ограничена двумя пересекающимися кривыми y=f1(x) и y=f2(x) и прямыми x=a и x=b, где a £ x £ b и f1(x)£ f2(x), то её площадь находится по формуле
Если фигура ограничена двумя пересекающимися кривыми y=f1(x) и y=f2(x) и прямыми x=a и x=b, где a £ x £ b и f1(x)£ f2(x), то её площадь находится по формуле
 b У y=f2(x)
b У y=f2(x)
S=ò[f2(x)-f1(x)] dx

 a S
a S
y=f1(x)
 |
 a b Х
a b Х
5. Если кривая, заданная уравнением y=f(x) на отрезке [a,b], пересекает ось Ох в точках х1 и х2 и располагается между этими точками под осью Ох, то вся площадь фигуры, заключённой между кривой, соответствующей этому уравнению, осью Ох и прямыми x=a и x=b,выразится так:
 У
У
x1 x2 b b

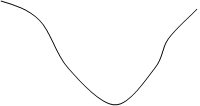
 S = òf(x)dx + ò½f(x)½dx + òf(x)dx = ò½f(x)½dx
S = òf(x)dx + ò½f(x)½dx + òf(x)dx = ò½f(x)½dx
a x1 x2 a
 О x1 x2 Х
О x1 x2 Х
a b
1. Вычислить площадь фигуры, ограниченной кривой y=x2+1, прямыми x=-1, x=2
Решение: Построим данную фигуру. Площадь фигуры ABCD находим по формуле
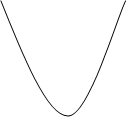
 b У
b У
S=òf(x) dx, где f(x)=x2+1, a=-1, b=2.
 a
a
Следовательно, B C
 2 2
2 2
S=ò(x2+1) dx=( +x)½= (
+x)½= ( +2)-(-
+2)-(- 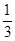 -1)= 6 (кв.ед.)
-1)= 6 (кв.ед.)
-1 -1
 А D
А D
-1 2 Х
2. Вычислить площадь фигуры, ограниченной линиями y=x2-6x+9 и y=x-1
Решение. Данная фигура ограниченна параболой y=x2-6x+9 и прямой y=x-1.
Определим точки пересечения этих линий, решив систему уравнений
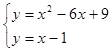
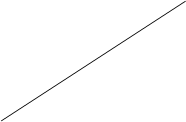 Находим
Находим
x2-6x+9=x-1
 x2-7x+10=0 Þ x1=5, x2=2, y1=4, y2=1
x2-7x+10=0 Þ x1=5, x2=2, y1=4, y2=1
Построим данную фигуру.
 Используем для нахождения искомой площади
Используем для нахождения искомой площади

 формулу
формулу
b 2 5 x
S=ò[f2(x)-f1(x)] dx
a
где f1(x)=x2-6x+9, f2(x)=x-1, a=2, b=5.
5 5
Тогда S=ò(x-1-x2+6x-9) dx=(-  +
+ 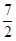 x2-10x)½=-
x2-10x)½=-  +7
+7 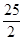 -
-
2 2
- 50+  +20=4,5 (кв. ед.).
+20=4,5 (кв. ед.).
3. Найти площадь фигуры, ограниченной линиями х=Öу, х=0, у=4.
Решение: Построим заданные линии.
Y
Так как полученная криволинейная трапеция прилежит к
 оси Оу, то применим формулу
оси Оу, то применим формулу
 d _
d _
 4 S=òj(y) dy, где j(y)=Öy, c=0, d=4
4 S=òj(y) dy, где j(y)=Öy, c=0, d=4
 S=
S= 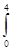 Öy dx=
Öy dx= 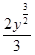 ½=
½= 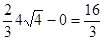
0 Х
1
4. Найти площадь фигуры, ограниченной линиями у=-х2, у=х-2, у=0
Решение: Построим заданные линии.

Y Из чертежа видно, что искомая площадь S
криволинейного треугольника OAB может
|
|
|

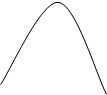
 0 1 2 x рассматриваться как площадь над кривой OAB на
0 1 2 x рассматриваться как площадь над кривой OAB на
C B отрезке [0,2].Однако указанная кривая задаётся не
одним уравнением.
A Поэтому разобъём криволинейный DOAB на
части, проецируя т.А на ось Ох.
у=-х2 Тогда S=SOAC+SCAB. Абсциссы точек О,А,В
задают пределы интегрирования.
у=х-2 1 1
SOAC=ò½-x2½ dx=½-  ½½=½-
½½=½- 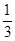 ½=
½= 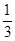
02 0 2
SCAB=ò½x-2½dx=½x2/2-2x½½=½2-4-  +2½=
+2½= 
1 1
S=  (кв. ед.)
(кв. ед.)
|
|
|



