 |
Фазометр с преобразованием сигналов
|
|
|
|
в прямоугольное напряжение
Принцип работы фазометра основан на том, что в двух совершенно идентичных каналах исследуемые напряжения усиливаются и ограничиваются (рис. 9.2, а). Эти прямоугольные колебания подаются на суммирующий каскад, а затем на линейный детектор и магнитоэлектрический прибор. Показания прибора пропорциональны фазовому сдвигу j, причем при 
; при 
, а при 
.
Форма сигналов в цепях фазометра при различных фазовых сдвигах показана на рис. 9.2, б.
| б) |
Рис. 9.2. Фазометр
Измерения фазового сдвига с помощью осциллографа
К осциллографическим методам измерения фазового сдвига относят методы линейной развертки, эллипса и круговой развертки.
Метод линейной развертки. Используется двухлучевой осциллограф. На входы V подаются напряжения 
и 
, фазовый сдвиг которых необходимо определить. Частота развертки подбирается такой, чтобы на экране наблюдалось 1,5 – 2 периода исследуемого сигнала (рис. 9.3).
Амплитуды сигналов подбираются одинаковыми, тогда непосредственно по шкале осциллографа можно определить
,
где ab и ас – измеренные на экране длины отрезков.
Причинами погрешности измерений в данном случае являются смещение оси, толщина светового луча, неточность определения ab и ас.
Метод эллипса. Существует ряд методов определения фазового сдвига по интерференционной фигуре на экране осциллографа при подаче на вертикально и горизонтально отклоняющие пластины синусоидального напряжения (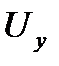
и 
).
| 
|
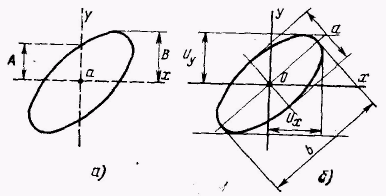
| Рис. 9.3. Метод линейной развертки | Рис. 9.4. Метод эллипса |
Метод 1. Угол j определяется из выражения 
.
Величины А и В показаны на рис. 9.4, а. Метод несколько неудобен из-за неточности определения центра эллипса О, но зато эта формула не зависит от отношения напряжени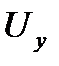й и .
|
|
|
Метод 2. (рис. 9.4, б). При условии = ,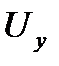 
, где а – малая ось эллипса, b – его большая ось.
Метод 3. При любых значениях 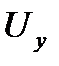и
,
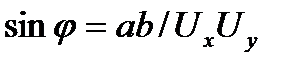где значения a, b, 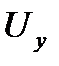и определяются на экране ЭЛТ осциллографа (рис. 9.4, б).
При всех трех методах определение фазового сдвига по интерференционной фигуре – эллипсу знак угла остается неопределенным. По наклону эллипса (рис. 9.5) можно определить приблизительное значение фазового сдвига. Погрешность измерения методами эллипса составляет 5 – 10 % из-за неточности определения длин отрезков, деформации эллипса.
Рис. 9.5. Фигура Лиссажу
Компенсационный метод
На рис. 9.6 приведена схема измерения фазового сдвига компенсационным методом. Напряжение источника U одновременно подается на исследуемый четырехполюсник и фазовращатель. Он позволяет плавно регулировать величину фазового сдвига и по шкале отсчитать его значение.
Выходные напряжения четырехполюсника 
и фазовращателя 
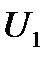подаются на индикатор равенства фаз. В качестве индикатора может быть использован осциллограф. Очевидно, что при равенстве фаз напряжений 
и 
.
Поскольку отсчет ведется по шкале фазовращателя, а осциллограф лишь является индикатором равенства, точность измерения может быть значительно повышена по сравнению с интерференционными методами. Она будет в основном погрешностью градуировки фазовращателя.
Рис. 9.6. Компенсационный метод
Фазовращатель. Наиболее часто применяются фазовращатели, построенные с использованием RC -цепей (рис. 9.7, а). Векторная диаграмма фазовращателя показана на рис. 9.7, б. Диаметр изображенной полуокружности представляет собой входное напряжение 
, причем 
, так как R1 = R2. В этом случае точка с является центром окружности. Вектор ad изображает напряжение на конденсаторе С, a ab – на резисторе R. При изменении сопротивления резистора R вектор cd будет изменять лишь фазу, оставаясь по величине неизменным и равным 
.
|
|
|
При R = 0 вектор cd будет совпадать по фазе с напряжением 
, а при 
, точка d совпадает с точкой а и 
по фазе сдвинуто относительно 
на 180°. Значение фазового сдвига в зависимости от элементов фазовращателя определяется выражением 
,
где 
– частота сигнала, С – емкость сигнала, R – сопротивление переменного резистора.
Рис. 9.7. Фазовращатель
Погрешность фазовращателя не превышает десятых долей градуса при условии, что сопротивление нагрузок, подключаемых к точкам cd, бесконечно велико или, по крайней мере, много больше величины сопротивлений, входящих в схему фазовращателей. Важен и тот факт, что величина фазового сдвига фазовращателя зависит от частоты подведенного сигнала. Построение схем фазовращателей, позволяющих получить постоянный фазовый сдвиг в диапазоне частот, связано с трудностями и поэтому не рассматривается
|
|
|
