Метод наложения (суперпозиции).

Метод преобразования D сопротивлений в эквивалентную звезду.

 

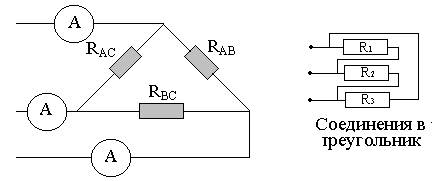Этим методом пользуются, если схему нельзя свернуть. Треугольник считается эквивалентным звезде, если токи в питающих проводах одинаковы.

 

 

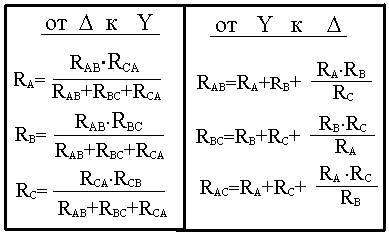Потери напряжения в линиях электропередач.

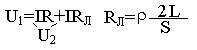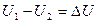
_DU_ГОСТ=>_DU=IR_Л

 

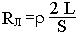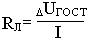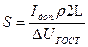- Округляют до большего стандартного сечения

 

Методы расчета сложных Э/Ц.

Сложная цепь –это цепь с несколькими источниками соединенными между собой ни последовательно, ни параллельно, ни смешанно.

Метод узлового напряжения.

Он применяется для расчёта сложных Э/Ц с двумя узлами.

1.Произвольно выбираем направление токов в ветвях.

2.Находим междуузловое напряжение.

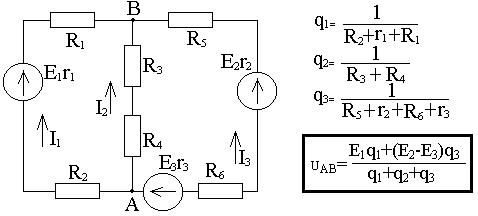; i- число ветвей с источниками -2;

n=3 – общее число ветвей.

φ _A= φ _B+I₁(R₂+r₁+R₁)-E₁

φ _A= φ _B+I₂(R₃+R₄)

φ _A= φ _B+I₃(R₅+r₂+R₆+r₃)-E₂+E₃

φ _A- φ _B= U_AB=I₁(R₂+r₁+R₁)-E₁

φ _A- φ _B= U_AB=I₂(R₃+R₄)

φ _A- φ _B= U_AB=I₃(R₅+r₂+R₆+r₃)-E₂+E₃

Метод уравнений Кирхгофа.

порядок составления уравнений:

1.Произвольно выбираем направления токов в ветвях.

2.Произвольно выбираем направления обхода контуров.

3.Составляем уравнения по 1-му закону Кирхгофа (на 1 меньше, чем число узлов в схеме).

 

 

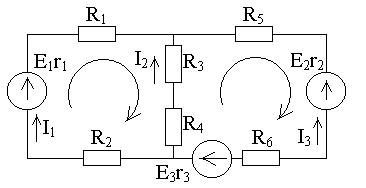
4.Недостающие уравнения составляем по 2-му закону Кирхгофа (всего уравнений столько, сколько ветвей в схеме).

I₁+I₂+I₃=0

E₁=I₁(R₁+r₁+R₂) - I₂(R₃+R₄)

E₃-E₂=I₂(R₃+R₄) - I₃(R₅+r₂+R₆+r₃)

 

I₁+I₂+I₃=0

E₁=I₁(R₄+R₁)-I₂(R₃+r₁)

E₂-E₁=I₂(R₂+r₁)-I₃(R₃+r₂)

 

Метод контурных токов.

Контурный ток-это нереальный, условный ток, который протекает по всем элементам данного контура.

1.Определяем количество независимых контуров в схеме. (независимый контур –

– это контур, в который входит хотя бы одна ветвь, не входящая ни в один, другой контур.)

2.Произвольно выбираем направление контурных токов.

3.Составляем уравнения по 2-му закону Кирхгофа для каждого независимого контура (необходимо учитывать падение напряжения в смежных ветвях от соседнего контурного тока).

4.Решаем систему уравнений и находим контурные токи.

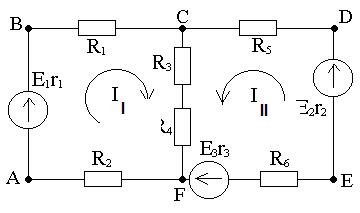5.Находим реальные токи в ветвях.

 

E₁=I_I(R₁+R₂+R₃+R₄+r₁)+I_II(R₃+R₄)

E₂-E₃=I_II(R₃+R₄+R₅+R₆+r₂+r₃)+I_I(R₃+R₄)

I₁= I_I I₂= (I_I-I_II) I₃= I_{II, т.е. реальные токи во внешних ветвях равны или равны, но противоположны соответствующим контурным токам, а во внутренних ветвях они находятся как алгебраическая сумма соседних контурных токов.}

 

Метод эквивалентного генератора.

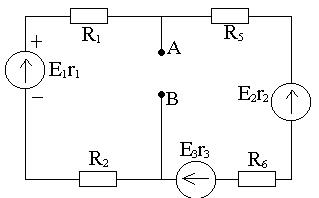
Он применяется, если изменяются параметры одного элемента. Из схемы убирают этот элемент и рассчитывают напряжение между зажимами «A»и «B». А так как при отсутствии резистора R₃ будет наблюдаться холостой ход относительно зажимов АВ, то следовательно 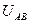будет численно равна ЭДС эквивалентного генератора. Далее рассчитывается эквивалентное сопротивление генератора, оно будет равно сопротивлению всей цепи, относительно зажимов АВ.

 

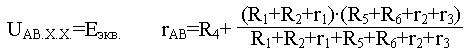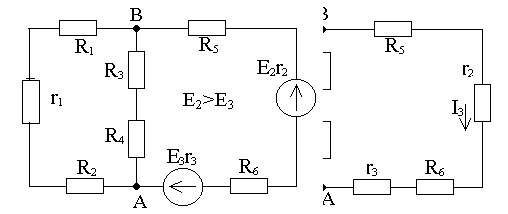
Метод наложения (суперпозиции).

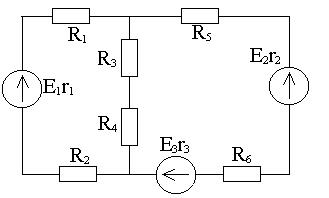
Он применяется, когда схема содержит не более трех ветвей с источниками. Сложная цепь заменяется столькими простыми цепями, сколько ветвей с источниками. Каждая простая цепь рассчитывается методом свёртывания. Определяются частичные токи в ветвях. Далее мысленно накладываем одну простую цепь на другую и находим реальные токи в ветвях, как алгебраическую сумму соответствующих частичных токов.

 

 

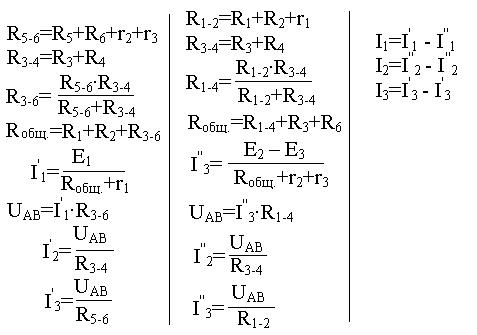ЧЕТЫРЕХПОЛЮСНИКИ.

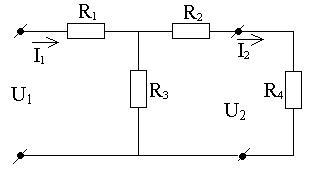
Распространенным элементом электрических цепей является четырехполюсник – часть схемы имеющая две пары зажимов, называемые обычно входными и выходными.Четырехполюсники могут быть активными (с источниками во внутренней схеме) и пассивными, линейными и нелинейными (содержащими нелинейные элементы во внутренней схеме). Примерами являются ЛЭП,трансформаторы, Эл. Фильтры, стабилизаторы, усилители и др. электротехнические устройства. Рассмотрим линейный пассивный четырехполюсник

; -это входные напряжение и ток, а ; 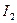-это выходные напряжение и ток. Между входными и выходными величинами в четырехполюснике существует жесткая связь, которая описывается уравнениями четырехполюсника:

U₁=AU₂+BI₂ уравнения

I₁=CU₂+DI₂ четырехполюсника

 

A, B, C, D – постоянные коэффициенты данного четырёхполюсника.

Свойства коэффициентов четырехполюсника: AD-BC=1

Пассивный четырёхполюсник:

1.Опытный метод определения коэффициентов четырёхполюсника.

 

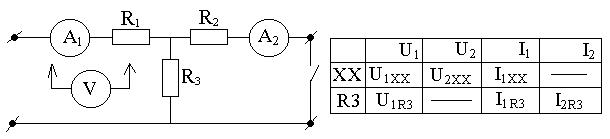2.Расчётный метод коэффициентов четырёхполюсника.

Коэффициенты определяются при помощи законов Ома и Кирхгофа.

 

 

 

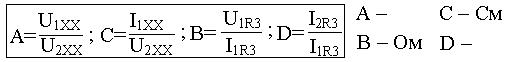Поделиться:

Воспользуйтесь поиском по сайту: