Тема №5: Обработка результатов измерений

Целью обработки результатов измерений является установление значения измеряемой величины и оценка погрешности полученного результата измерения. Методы обработки ре­зультатов наблюдений могут быть разными в зависимости от пред­варительной информации, которой располагает экспериментатор об источниках и характере проявления погрешностей, условиях эксперимента, свойствах используемых средств измерений, от вида измерений, числа выполненных наблюдений и других причин.

Рассмотрим наиболее характерные случаи обработки результа­тов наблюдений при различных видах измерений.

Прямые измерения. Предположим, что при многократном из­мерении интересующей нас величины получили n отдельных ре­зультатов наблюдений. Исключив систематическую погрешность из каждого наблюдения, получаем исправленный ряд значений х₁, х₂,.., х_n, математическим ожиданием которого является дей­ствительное значение измеряемой величины. За действительное значение измеряемой величины принимаем среднее арифмети­ческое

=

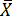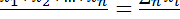
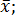Отклонения между отдельными значениями наблюдений и сред­ним арифметическим (разности p₁ = x ₁- ; p₂ = x₂- ...; p_n = x_n- 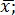)называются рассеянием результатов в ряду измерений, или оста­точными погрешностями. Они могут быть как положительными, так и отрицательными. На основании свойства среднего арифме­тического алгебраическая сумма остаточных погрешностей равна нулю, т.е. 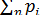= 0. Этим следует пользоваться для контроля правильности подсчета .

Если дисперсия полученного ряда наблюдений известна из предыдущих экспериментов или из технической документации на применяемые средства измерений, то дисперсию среднего арифметического можно определить по формуле σ²[ 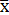] = , где

σ²[ 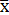] — дисперсия действительного значения (среднего арифме­тического) измеряемой величины этого ряда; 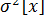— дисперсия исправленного ряда наблюдений.

Если дисперсия ряда неизвестна, то ее оценку можно найти по формуле

S² = ,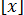

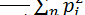где p_i — остаточные погрешности исправленного ряда наблюде­ний.

В этом случае за оценку дисперсии действительного значения измеряемой величины принимают

 

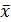S²[ ] = S² ,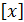

Для нахождения доверительного интервала погрешности изме­рения необходимо найти закон распределения для величины: при известной дисперсии —

( - х_и) / σ[ ];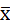

при неизвестной дисперсии —

( - х_и)/S .

 

Косвенные измерения. Допустим, что измеряемая величина у является функцией аргументов а, b, с, измеряемых прямыми измерениями, т.е. у = F(a, b, с,...). Проведя обработку ряда на­блюдений для каждого аргумента методом, изложенным для пря­мых измерений, можно найти оценки значений аргументов:

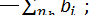A = ; B = C = …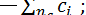

и оценки дисперсий А, В, С,...

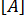S² = ; S² = ;

где п_а, п_b, п_с,... — число измерений соответствующего аргумента.

Дальнейшую обработку результатов наблюдений можно про­водить по-разному. Наиболее распространенным является метод линеаризации, основанный на разложении функциональной за­висимости Y = F(A, В, С,...) в ряд Тейлора с ограничением ряда членами, содержащими первые производные:

Y = Y_и + 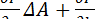𝛥B + ,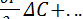

где Y_и — действительное значение косвенно измеряемой величины; 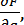значения частных производных от функции по соответствующему аргументу в точке, где аргументы име­ют действительное значение; 𝛥А, 𝛥В, 𝛥С,... — погрешности ре­зультата измерения соответствующего аргумента.

В правой части выражения случайными величинами яв­ляются 𝛥А, 𝛥В, 𝛥С,... Если результаты измерения аргументов не зависят друг от друга (что чаще всего и бывает на практике), то эти случайные величины являются независимыми.

Совместные измерения. Целью совместных измерений является установление функциональной зависимости между величинами, например зависимости сопротивления от температуры. Отыски­вая зависимость между величинами а и b, необходимо устанавли­вать и измерять различные размеры величины а и одновременно измерять величину Ь. Таким образом, можно получить координа­ты исследуемой зависимости а₁ b₁; а₂, b₂, а_n, b_п. Так как ре­зультаты измерения этих величин содержат погрешности, то по­лученные координаты не будут принадлежать истинной исследу­емой зависимости. Исключив систематическую погрешность из каж­дого результата измерения, можно уточнить эти координаты, но и уточненные координаты все-таки будут отклоняться (рассеи­ваться) относительно истинной зависимости из-за случайных по­грешностей.

Степень рассеивания характеризуется дисперсией. Правильной зависимостью, построенной по полученным координатным то­чкам, следует считать такую зависимость, при которой дисперсия координатных точек относительно этой зависимости будет мини­мальной. Для оценки дисперсии нужно вычислить сумму квадра­тов отклонений координатных точек от истинной зависимости. Минимальной дисперсии будет соответствовать минимальное зна­чение суммы квадратов этих отклонений. Поэтому метод, с помо­щью которого отыскивается истинная зависимость, называется методом наименьших квадратов.

Суммирование погрешностей. В практике измерений часто вста­ет задача определения результирующей (суммарной) погрешно­сти по известным значениям составляющей этой погрешности.

При рассмотрении составляющих погрешности как случайных величин, результирующую погрешность следует определять по правилу суммирования случайных величин. Это правило основано на известных из теории вероятности положениях:

1)математическое ожидание (систематическая погрешность) результирующей погрешности определяется алгебраической сум­мой математических ожиданий (систематических погрешностей) составляющих;

2)дисперсия результирующей погрешности определяется вы­ражением

=

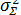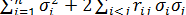
где п — число суммируемых составляющих погрешностей; 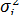— дисперсия i-й составляющей погрешности; 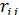— коэффициент корреляции между j-й и i-й составляющими (знак i < j под сум­мой означает, что суммирование распространяется на все воз­можные попарные сочетания составляющих, для которых i < j).

Нахождение результирующей систематической погрешности по известным систематическим погрешностям суммируемых состав­ляющих не вызывает трудностей. Использование же выражения для расчета затруднительно, так как точное значение ко­эффициента корреляции между составляющими обычно неизвест­но. В этом случае при расчетах полагают r равным нулю, если слу­чайные составляющие можно считать независимыми, или равным единице со знаком «+» или «-», если заметна корреляция между суммируемыми случайными составляющими погрешностей. Рассмот­рим подробнее суммирование случайных погрешностей.

Суммирование случайных погрешностей при нормальных законах их распределения. Будем считать, что результирующая погрешность измерения состоит из п случайных составляющих, имеющих нор­мальный закон распределения, ±δ_im — границы доверительного интервала i-й случайной составляющей.

Зная доверительную вероятность и доверительный интервал для каждой составляющей погрешности, можно найти среднее квадратическое отклонение каждой из них по формуле

= δ_im/ɀp_i,

где ɀp_i — коэффициент, взятый из таблиц для нормального рас­пределения и соответствующей доверительной вероятности Р_i.

Если для суммируемых составляющих погрешностей известны их предельные значения, то предельное значение результирующей погрешности находят путем арифметического суммирования пре­дельных значений составляющих.

Суммирование случайных погрешностей при законах распреде­ления, отличных от нормального. Трудность нахождения суммар­ной погрешности в этом случае заключается в том, что закон ее распределения зависит от конкретных видов и характеристик за­конов распределения суммарных составляющих. Например, при сложении двух независимых случайных погрешностей, имеющих равномерные законы распределения с одинаковыми дисперси­ями, результирующая погрешность будет распределяться по тре­угольному закону. Если же эти равномерные законы имеют разные дисперсии, то результирующая погрешность будет распределять­ся по трапецеидальному закону. Поэтому для установления дове­рительного интервала результирующей погрешности необходимо в каждом конкретном случае искать методами теории вероятно­стей закон распределения результирующей погрешности.

Зная закон распределения результирующей погрешности, мож­но найти доверительный интервал этой погрешности по выраже­нию, аналогичному:

δ_Σ = ± ,

где 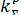— коэффициент, зависящий от закона распределения ре­зультирующей погрешности с доверительной вероятностью Р.

Возможны приближенные способы определения доверитель­ного интервала суммарной погрешности без установления закона распределения результирующей погрешности.

Первый способ базируется на центральной предельной теоре­ме: если число суммируемых независимых составляющих доста­точно велико (практически при п > 5), то закон распределения результирующей погрешности близок к нормальному и в качестве коэффициента 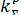можно принимать ɀp_.

Второй способ основан на экспериментальном исследовании, показавшем, что при суммировании независимых составляющих, имеющих симметричные законы распределения, можно пользо­ваться приближенными значениями :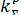

при доверительной вероятности Р = 0,90 коэффициент 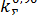= 1,6;

при доверительной вероятности Р= 0,95 коэффициент 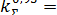1,8.

При этом погрешность в определении δ_Σ не превышает ±10 %.

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: