 |
Первый признак сравнения рядов.
|
|
|
|
Пусть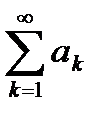 
и 
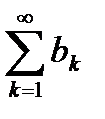– два знакоположительных числовых ряда и выполняется неравенство 
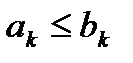для всех k = 1, 2, 3,... Тогда из сходимости ряда 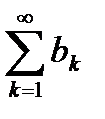следует сходимость 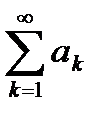, а из расходимости ряда 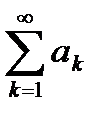следует расходимость .
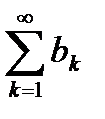Второй признак сравнения.
Пусть 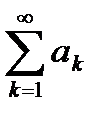и 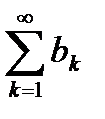– знакоположительные числовые ряды. Если 
, то из сходимости ряда 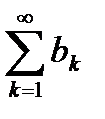следует сходимость 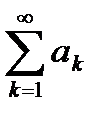. Если 
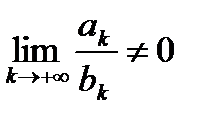, то из расходимости числового ряда 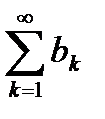следует расходимость .
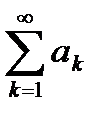Третий признак сравнения.
Пусть 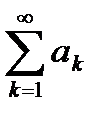и 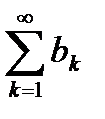– знакоположительные числовые ряды. Если с некоторого номера N выполняется условие 
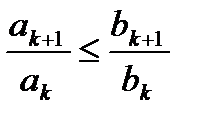, то из сходимости ряда 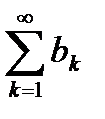следует сходимость 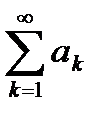, а из расходимости ряда 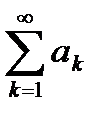следует расходимость .
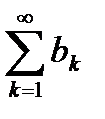Признак Даламбера.
Пусть 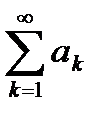– знакоположительный числовой ряд. Если 
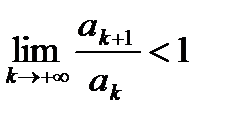, то числовой ряд сходится, если 
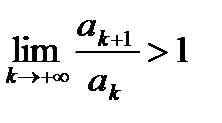, то ряд расходится.
Замечание.
Признак Даламбера справедлив, если предел бесконечен, то есть, если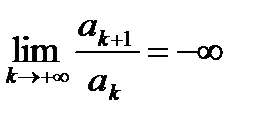 
, то ряд сходится, если 
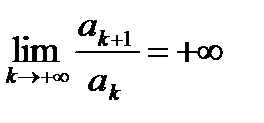, то ряд расходится.
Если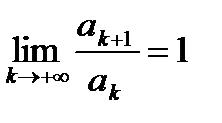 
, то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
Радикальный признак Коши.
Пусть 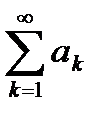– знакоположительный числовой ряд. Если 
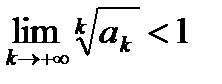, то числовой ряд сходится, если 
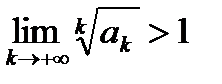, то ряд расходится.
Замечание.
Радикальный признак Коши справедлив, если предел бесконечен, то есть, если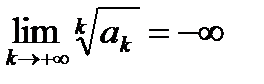 
, то ряд сходится, если 
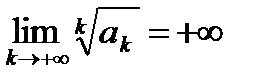, то ряд расходится.
Если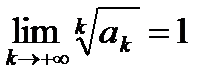 
, то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
Интегральный признак Коши.
Пусть 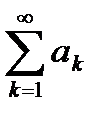– знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции 
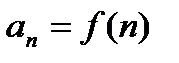. Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале [ a; +∞), где a ≥ 1). Тогда в случае сходимости несобственного интеграла 
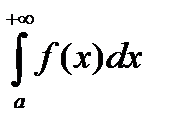сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.
|
|
|
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
Исследовать сходимость рядов:
1) 
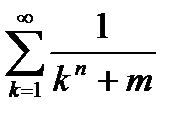
2) 
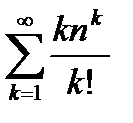
3) 
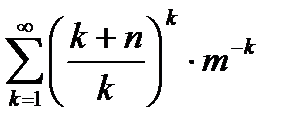
4) 
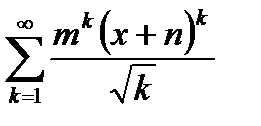
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Признаки сходимости.
2. Радиус и область сходимости.
3.
Практическая работа №17
Тема: Разложение функций в ряд.
Цель: Научиться раскладывать функцию в степенной ряд и применять его для приближенных вычислений с заданной точностью.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Если функция f (x) имеет непрерывные производные вплоть до (n +1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
,
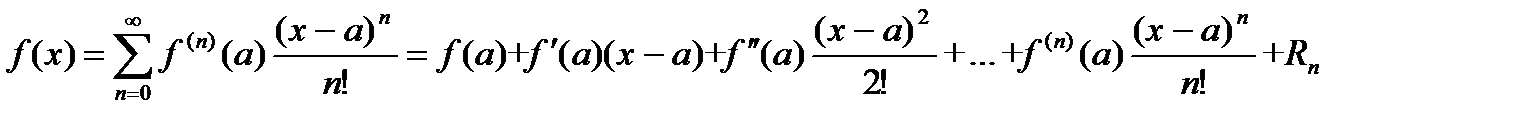где Rn − остаточный член в форме Лагранжа определяется выражением
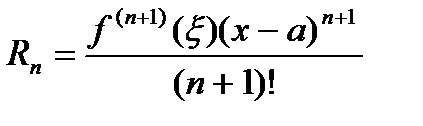, a < ξ < x.
Если приведенное разложение сходится в некотором интервале x, т.е.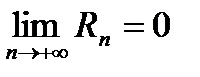 
, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
Если a = 0, то такое разложение называется рядом Маклорена:
.
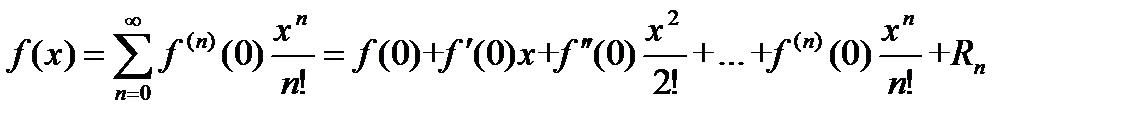Разложение некоторых функций в ряд Маклорена
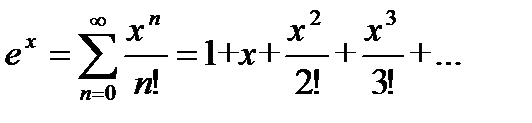
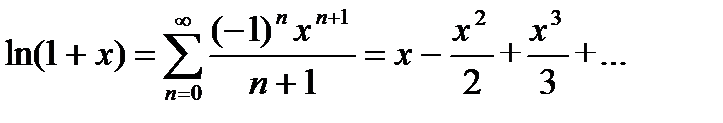, −1 < x ≤ 1.
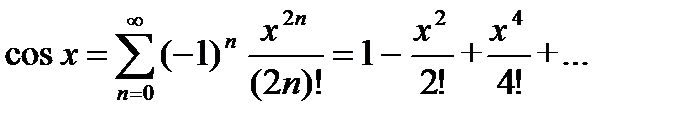
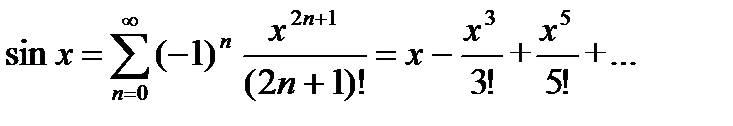
Ряд Фурье.
Говорят, что функция f (x) имеет период P, если f (x + P) = f (x) для всех значений x. Пусть период функции f (x) равен 2 π. В этом случае достаточно рассмотреть поведение функции в интервале [− π, π ].
1. Предположим, что функция f (x) с периодом 2 π абсолютно интегрируема в интервале [− π, π ]. При этом является конечным, так называемый интеграл Дирихле: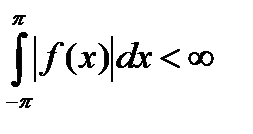 
;
2. Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).
|
|
|
Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции.
Ряд Фурье функции f (x) представляется в виде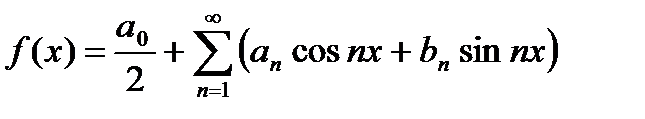 
,
где коэффициенты Фурье a 0, an и bn определяются формулами
, 
, 
.
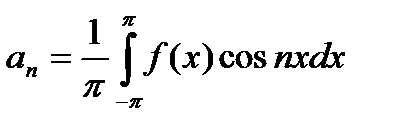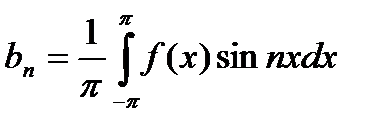Разложение в ряд Фурье четных и нечетных функций
Разложение в ряд Фурье четной функции f (x) с периодом 2 π не содержит синусов и имеет вид
,
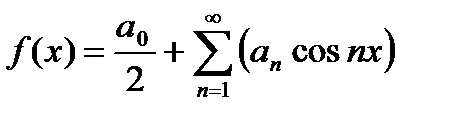где коэффициенты Фурье определяются выражениями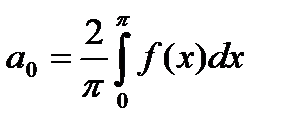 
, 
.
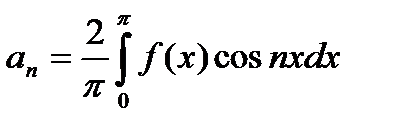Аналогично, разложение в ряд Фурье нечетной функции f (x), имеющей период 2 π, содержит только синусы и имеет вид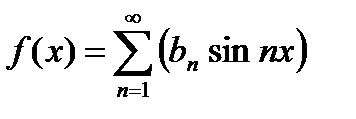 
,
где коэффициент равен 
.
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1) Используя разложение в ряд Маклорена, вычислите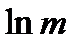 
с точностью до 
.
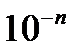2) Разложить в ряд Фурье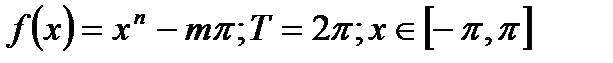 
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Ряд Тейлора и Маклорена.
2. Ряд Фурье.
3.
|
|
|
12 |
