 |
Введение иррационального числа. Методическая схема введения действительного числа
|
|
|
|
Следующее расширение понятия числа – иррациональное число. В соответствии с построением множества действительных чисел по Дедекинду на множестве рациональных чисел существуют только три вида сечений: 1) в В нет наибольшего, в В` наименьшее(деление множества рациональных чисел по числу, например,2); 2) в В есть наибольшее, в В` нет наименьшего; 3) в В нет наибольшего числа, в В` нет наименьшего
Пример. 
Докажем, что в В нет наибольшего числа.
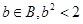. Покажем, что можно подобрать такое целое положительное число n, для которого 
, т.е.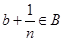 
- доказать. 
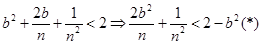Если для неравенства 
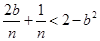найдётся n, для которого оно справедливо, то будет верно и данное неравенство: (*) 
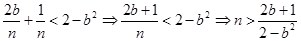, т.е. число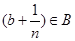 
Так как во множестве рациональных чисел существует сечение третьего типа, то оно не является полным. Это сечение определяет число иррациональное. С геометрической точки зрения этот факт означает, что на координатной прямой существуют точки, которые не соответствуют никаким числам из множества рациональных чисел: множество рациональных чисел несвязно.
В школе при введении иррационального числа используют следующий факт: известно, что каждому рациональному числу r соответствует единственная точка M(r) прямой l, на которой заданы: начало отсчета, направление и масштаб. При этом число 
называется координатой точки M. Верно ли обратное утверждение? Ответ иллюстрируется следующим примером:
Докажем, что точка М не соответствует никакому рациональному числу.
, что противоречит тому, что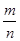 
- несократимая дробь определение рационального числа).
Ещё один способ доказательства иррациональности числа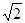 
является построение последовательных рациональных приближений этого числа по недостатку и по избытку, которые обладают следующими свойствами:
|
|
|
1) каждое число последовательности (2) больше числа последовательности (1) с тем же номером: 1,4; 1,41; 1,414; 1,4142;…. (1)
1,5; 1,42; 1,415; 1,4143;…. (2)
2) последовательность (1) 
; (2) - 
3) разность между членами последовательностей с одинаковыми номерами неограниченно уменьшается по абсолютной величине при увеличении номера и равна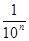 
. Геометрически этот факт определяет сближение точек последовательности к .
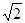Иначе говоря, члены последовательностей (1) и (2) образуют непериодическую десятичную дробь.
Методическая схема введения действительного числа:
а) делается попытка решения уравнения 
, т.е. необходимо доказать теорему: не существует ни целого, ни дробного числа, квадрат которого равнялся бы числу 2
б) так как теорема доказана, то надо показать, что не существует целого числа, квадрат которого равен 2;
в) параллельно вводится понятие действительного числа на геометрической основе, т.е. в процессе измерения отрезков (отыскание абсциссы точки графика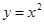 
, ордината которой равна 2). Такая задача приводит к проблеме измерения отрезка другим, принятым за единицу измерения;
г) измерение отрезка. Соизмеримые и несоизмеримые отрезки. Десятичные приближения длины отрезка;
д) бесконечные периодические и непериодические дроби;
е) обращение обыкновенной дроби в бесконечную периодическую и обратная задача;
ж) иррациональные числа. Примеры;
з) действительные числа;
и) сравнение действительных чисел;
к) операции над действительными числами.
Следует помнить, что если в заданиях для следующих выражений:
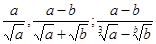необходимо избавится от иррациональности в знаменателе, это означает, что в знаменателях этих дробей находятся иррациональные числа. В этом учащиеся могут убедиться, придав буквам конкретные значения. Алгебраические категории представляют собой абстракции более высокого порядка, а значит, рассуждения в алгебре носят более обобщённый характер, нежели непосредственно в числовых системах.
|
|
|
Заключение
Изучение арифметики натуральных чисел основано на наглядности. Учащиеся должны твердо усвоить, что любое натуральное число может быть изображено точкой на координатном луче, но не всякой точке на этом луче отвечает натуральное число. Этот последний факт готовит учащихся к пониманию необходимости введения новых чисел. Учащиеся знакомятся с одним из свойств множества натуральных чисел – бесконечностью. При изучении законов арифметических действий, для избегания формализма необходимо отметить их теоретическое значение. В частности, коммутативный и ассоциативный законы умножения целесообразно связать с геометрическим материалом (вычислением площадей прямоугольников, объёмом прямоугольных параллелепипедов).
Литература
1. К.О. Ананченко «Общая методика преподавания математики в школе», Мн., «Унiверсiтэцкае»,1997г.
2. Н.М. Рогановский «Методика преподавания в средней школе», Мн., «Высшая школа», 1990г.
3. Г. Фройденталь «Математика как педагогическая задача»,М., «Просвещение», 1998г.
4. Н.Н. «Математическая лаборатория», М., «Просвещение», 1997г.
5. Ю.М. Колягин «Методика преподавания математики в средней школе», М., «Просвещение», 1999г.
6. А.А. Столяр «Логические проблемы преподавания математики», Мн., «Высшая школа», 2000г.
|
|
|
