Расчёт увеличения надёжности элементов.

 

По графику (рис.2) находим для  (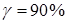) - процентную наработку системы

 

часов

 

Проверочный расчёт показывает, что при часов

По условиям задания повышенная - процентная наработка системы.

 

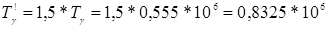 часов

 

Расчёт показывает, что при  для элементов преобразованной схемы (рис1.2)

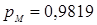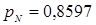, , . Следовательно, из 3-х последовательно соединённых элементов минимальное значение вероятности имеет элемент N (мост).

Для того, чтобы при ч. система в целом имела вероятность безотказной работы , необходимо чтобы элемент N имел вероятность безотказной работы:

 

 

Но при этом значении элемент N будет самым надёжным. Значит

 

 

Значит надо увеличивать надёжность 2-х элементов: 1 и N.

 

 

Увеличим надёжность моста. Для этого посчитаем значимость элементов A, B, C и D в нём.

 

 

Значит, важность(значимость) элементов B и C больше, значит их мы будем увеличивать.

Для нахождения минимально необходимой вероятности безотходной работы элемента 2 необходимо решить уравнение (1.6) относительно P₂ при Р_N=0,9574. Найдём его графически. График представлен на рис.3(по данным таблицы 7).

 

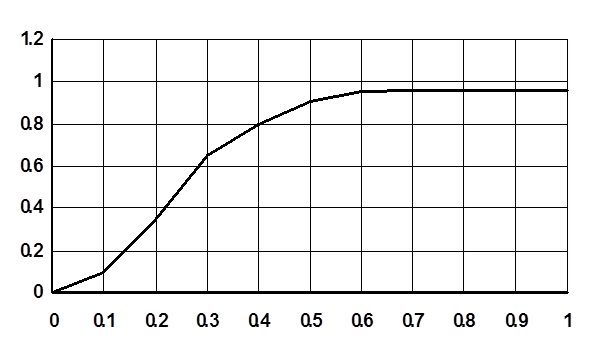
Рис.3

График зависимости вероятности безотказной работы моста N от вероятности без работы его элементов. По графику находим при P_N=0,9574

 

P₂=0,6875

 

Так как по условиям задания всё элементы работают в условиях нормальной эксплуатации и подчиняются экспоненциальному закону, то для элемента P₂ при t=0,8325*10⁶ ч., находим:

 

 

Таким образом, для увеличения -процентной наработки необходимо увеличить надёжность элементов 5, 6, 7 и 8 и снизить интенсивность их отказов с 1 до 0,45, то есть в 2,2 раза.

Результаты расчётов для системы с увеличенной надёжностью элементов B^!, С^! и 1 приведены в таблице 2, элемента N(моста) и системы S^! после повышения надёжности.

 

Таблица №2

Элемент	li, *10-6ч-1	Наработка t, * 106 ч.
		0,2	0,4	0,6	0,8	0,555	0,8325	1	1,2	1,4	1,8	2,0
2!	0,45	0,9139	0,8353	0,7634	0,6977	0,9297	0,6875	0,6376	0,5827	5326	0,4449	0,4066
A	-	0,994	0,9642	0,9082	0,8330	0,9512	0,8196	0,7474	0,6588	5724	0,4184	0,8335
B!, C!	-	0,9926	0,9729	0,9440	0,9086	0,9521	0,9024	0,8687	0,8259	7815	0,6918	0,6478
N!	-	0,9999	0,9977	0,9871	0,9602	0,9907	0,9539	0,9120	0,8429	7578	0,5677	0,4758
S!	-	0,9922	0,9502	0,9401	0,9144	0,9434	0,908	0,8686	0,8028	7217	0,5407	0,4532

 

 

График зависимости вероятности безотказной системы после увеличения надёжности элементов приведён на рис.2(кривая S^!).

 

Увеличение надёжности за счёт резервирования элементов.

 

Для элемента N(моста) резервирование означает увеличения большего числа элементов. B и C– наиболее значимые элементы в нём. Будем их улучшать наряду с первым элементом.

 

Для повышения надёжности моста добавляем параллельно к элементам B и C элементы до тех пор, пока вероятность безотказной работы квазиэлемента N не достигнет заданного значения.

 

P_N должна быть больше P_N=0,9539

1. Добавим параллельно по одному элементу к B и C

P_N=0,9522<0,9539

2. Добавляем ещё по одному

P_N=0,9687>0,9539

3. Добавим параллельно к первому элементу ещё один аналогичный:

P₁=1-(1-P₁)²=21-(1-0,9201)²=0,9936>0,9574

 

Результаты расчётов вероятностей безотказной работы системы N, 1 и системы в целом приведены в таблице 3.

Расчёты показывают, что при t=0б8325*10⁶ ч.

PS=0,9451>0,9, что соответствует условию задачи.

 

Таблица №3

Элемент	li, *10-6ч-1	Наработка
		0,2	0,4	0,6	0,8	1	0,8325	1,4	1,8	2,0
1	0,1	0,9802	0,9607	0,9417	0,9231	0,9048	0,9201	0,8693	0,8353	0,8187
2!!	-	0,8187	0,6703	0,5488	0,4493	0,3679	0,4350	0,2466	0,1653	0,1353
C!!, B!!	1,0	0,9998	0,9961	0,9813	0,8724	0,8991	0,833	0,7573	0,5948	0,5167
1!!	-	0,9996	0,9985	0,9966	0,9941	0,9909	0,9936	0,9829	0,9729	0,9671
N!!	-	0,9999	0,9995	0,9944	0,9323	0,9271	0,9687	0,7407	0,4962	0,3837
S!!	-	0,9984	0,9935	0,9813	0,9411	0,8954	0,9451	0,6940	0,4477	0,3390

 

На рис.2 представлена вероятность безотказной работы системы S^!! После структурного резервирования (кривая S^!!).

 

Схема после структурного резервирования представлена на рис. 4

 

Рис.4

Таким образом, для увеличения надёжности надо добавить элементы 16, 17, 18, 19, 20(рис.4).

 

Выводы

1. На рис. 2 представлена зависимость вероятности безотказной работы системы (кривая). Из графика видно, что 90% - наработка исходной системы составляет 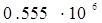часов.

2. Для повышения надежности и увеличения 50% - наработки системы в 1.5 раза (до часов) предложены два способа:

а) повышение надежности элементов 2, 3, 4, 5 и 6 и уменьшение их отказов с 1 до  ч;

б) нагруженное резервирование основных элементов 1, 2, 3, 4, 5 и 6 идентичными по надежности резервными элементами 16, 17, 18,19 и 20.

3. Анализ зависимостей вероятности безотказной работы системы от времени (наработки) показывает, что второй способ повышения надежности системы (структурное резервирование) предпочтительнее первого, так как в период наработки до  часов вероятность безотказной работы системы при структурном резервировании (кривая) выше, чем при увеличении надежности элементов (кривая).

 

 

12	Поделиться:

Воспользуйтесь поиском по сайту: