Второй закон излучения Вина

В 1896 году Вин на основе дополнительных предположений вывел второй закон:

U_v=C₁V³e^-C2*(V/T)

где uν — плотность энергии излучения
ν — частота излучения
T — температура излучающего тела
C1,C2 — константы.
Опыт показывает, что вторая формула Вина справедлива лишь в пределе высоких частот (малых длин волн). Она является частным конкретным случаем первого закона Вина.
Позже Макс Планк показал, что второй закон Вина следует из закона Планка для больших энергий квантов, а также нашёл постоянные C1 и C2. С учётом этого, второй закон Вина можно записать в виде:

U_v=(8пhV³/C³)e^-hv/kT

где uν — плотность энергии излучения
ν — частота излучения
T — температура излучающего тела
h — постоянная Планка
k — постоянная Больцмана
c — скорость света в вакууме

Интенсивность излучения абсолютно чёрного тела в зависимости от температуры и частоты определяется законом Планка:

I(v)=((2пhV³)/C²)*(1/(e^hv/kT-1))

где I(ν)dν — мощность излучения на единицу площади излучающей поверхности в диапазоне частот от ν до ν + dν.
Эквивалентно,

U(лямбда)=(2пhC²/лямбда⁵)*(1/(e^hv/kT-1))
где u(λ)dλ — мощность излучения на единицу площади излучающей поверхности в диапазоне длин волн от λ до λ + dλ.

74) ФОТОЭФФЕКТ, группа явлений, связанных с "освобождением" электронов твердого тела от внутриатомной связи под действием электромагнитного излучения. Различают: 1) внешний фотоэффект, или фотоэлектронная эмиссия, - испускание электронов с поверхности твердого тела под действием света, g-излучения и др. (открыт Г. Герцем в 1887, объяснен А. Эйнштейном); 2) внутренний фотоэффект - то же, что фотопроводимость; 3) вентильный фотоэффект - возбуждение светом эдс на границе между металлом и полупроводником или между разнородными полупроводниками.

Рождение квантовой механики, пожалуй, естественнее отнести к моменту написания Эйнштейном закона сохранения энергии для внешнего фотоэффекта, где Эйнштейн использовал выводы из формулы Планка:

hv=A_вых+mU²/2
Эйнштейн доверился результату Планка, состоящему в том, что при взаимодействии с веществом энергия электромагнитного излучения может поглощаться порциями - квантами, величина которых равна hν, таким образом, можно предположить, что поле ведет себя как поток частиц.
Квант с энергией hν выбивает с поверхности металла электрон, затрачивая на это энергию, равную работе выхода электрона из этого металла Авых, оставшаяся энергия кванта идет на сообщение электрону кинетической энергии.mU²/2
Уравнение Эйнштейна для фотоэффекта объяснило все экспериментальные результаты по выбиванию электронов лучами света с поверхности металлов, в том числе наличие «красной» границы фотоэффекта, которое (наличие) не могло быть объяснено по законам классики.

Применение:
1. Кино: воспроизведение звука
2. Фототелеграф.
3. Фотометрия: для измерения силы света, яркости, освещенности.
4. Управление производственными процессами.

II внутренний фотоэффект используется в фоторезисторах
Фоторезистор – устройство, сопротивление которого зависит от освещенности.
Механизм внутреннего фотоэффекта. При попадании излучения внутрь вещества происходят два явления. Одни кванты излучения, поглощаясь атомами (или ионами), увеличивают кинетическую энергию их теплового движения, поэтому вещество нагревается. Другие кванты излучения, поглощаясь атомами, производят фотоионизацию, в результате чего в веществе образуются дополнительные носители заряда – электроны проводимости и дырки. Их образование ведет к уменьшению электрического сопротивления.
Используется при автоматическом управлении электрическими цепями с помощью световых сигналов и в цепях переменного тока.

75) Эффект Комптона: При длине волны l<0,4 мкм, мы переходим в ультрафиолетовую область света. При этом переходе в области РИ (рентгеновского излучения) и гамма излучения, наблюдается так называемый эффект Комптона:

Особенно отчетливо проявляются корпускулярные свойства света в явлении, которое получило название эффект Комптона. В 1923г. А Комптон, исследуя рассеяние рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах наряду с излучением первоначальной длины волны l содержатся также лучи большей длины волны . Разность оказалась зависящей только от угла q, образуемого направление рассеянного излучения с направлением первичного пучка.

Эффект Комптона (рис 4)

еупругое соударение гамма-кванта с покоящимся электроном, в результате которого изменяется энергия электрона и гамма кванта.
Для объяснения закона фотоэффекта необходимо использовать закон сохранения импульса и закон сохранения энергии:

 

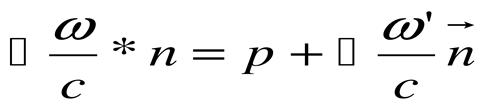
где: ;

 

 

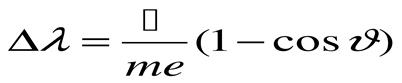
где J - угол, на который откланяется квант.

КОМПТОНОВСКАЯ ДЛИНА ВОЛНЫ
величина размерности длины, характерная для релятив. квант. процессов; выражается через массу т ч-цы и универсальные постоянные А и с: l0=h/mc. Назв. К. д. в. связано с тем, что l0 определяет изменение длины волны Dl эл.-магн. излучения при комптоновском рассеянии на эл-не (см. КОМПТОНА ЭФФЕКТ). Чаще К. д. в. называют величину l0=ћ/mc. Для эл-на l0»З,9•10-11 см, для протона l0»2,1•10-14 см.
К. д. в. определяет масштаб пространств. неоднородностей полей, при к-рых становятся существенными квант. релятив. процессы. Напр., если рассматривается эл.-магн. поле, длина волны к-рого l меньше К. д. в. эл-на, то энергия квантов этого поля?=hn (где n=c/l — частота) оказывается больше, чем энергия покоя эл-на mec2((?=hc/l>mee2), и, следовательно, в этом поле становятся существенны процессы рождения электрон-познтронных пар, к-рые описываются релятив. квант. теорией поля.
К. д. в. определяет также расстояние, на к-рое может удалиться виртуальная частица массы т от точки своего рождения. Поэтому радиус действия яд. сил (определяемый самыми лёгкими из виртуальных адронов — p-мезонами) по порядку величины равен К. д. в. p-мезона (=10-13 см). Аналогично поляризация вакуума за счёт рождения виртуальных электрон-позитронных пар проявляется на расстояниях порядка К. д. в. эл-на.

76) КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ
лежащее в основе квант. теории представление о том, что в поведении микрообъектов проявляются как корпускулярные, так и волн. черты. По представлениям классич. (неквантовой) физики, движение ч-ц и распространение волн — принципиально разные физ. процессы. Однако опыты по вырыванию светом эл-нов с поверхности металлов (фотоэффект), изучение рассеяния света на эл-нах (Комптона эффект) и результаты ряда др. экспериментов убедительно показали, что свет — объект, имеющий, согласно классич. теории, волн. природу, обнаруживает сходство с потоком ч-ц — фотонов, обладающих энергией? и импульсом р, к-рые связаны с частотой v и длиной волны К света соотношениями:?=hv, p=h/l. С др. стороны, пучок эл-нов, падающих на кристалл, даёт дифракц. картину, к-рую можно объяснить лишь на основе волн. представлений: со свободно движущимся эл-ном сопоставляется т. н. волна де Бройля, длина волны и частота к-рой связаны соотношениями
l=h/p, v=?lh,
где р — импульс,? — энергия эл-на.
Позже было установлено, что это явление свойственно вообще всем микрочастицам (см. ДИФРАКЦИЯ МИКРОЧАСТИЦ). Такой дуализм корпускулярных и волн. св-в не может быть понят в рамках классич. физики; так, возникновение дифракц. картины при рассеянии ч-ц несовместимо с представлением о движении их по траекториям. Естеств. истолкование К.-в. д. получил в квантовой механике.

Двойственная природа света: Впервые проблема корпускулярно-волнового дуализма проявила себя при исследовании природы света. В XVII веке Исаак Ньютон предложил считать свет потоком мельчайших корпускул. Это позволяло просто объяснить ряд наиболее характерных свойств света – например, прямолинейность световых лучей и закон отражения, согласно которому угол отражения света равен углу падения. Вообще, вся геометрическая оптика прекрасно согласуется с корпускулярной теорией света. Но явления интерференции и дифракции света никак в эту теорию не вписывались. Объяснить их ученым удалось лишь в XIX веке создателям волновой теории света. А теория электромагнитного поля и знаменитые уравнения Максвелла, казалось бы, вообще поставили точку в этой проблеме. Оказалось, что свет – это просто частный случай электромагнитных волн, то есть процесса распространения в пространстве электромагнитного поля. Мало того, волновая оптика объяснила не только те явления, которые не объяснялись с помощью корпускулярной теории, но и вообще все известные к XIX веку световые эффекты. И все законы геометрической оптики тоже оказалось возможным доказать в рамках волновой оптики.
Однако уже в самом начале XX века опять возродилась корпускулярная теория света, так как были обнаружены явления, которые с помощью волновой теории объяснить не удавалось. Это – давление света, фотоэффект, Комптон-эффект и законы теплового излучения. В рамках корпускулярной теории эти явления прекрасно объяснялись, и корпускулы (частицы) света даже получили специальное название. Макс Планк назвал их световыми квантами (по-русски – порциями), а Альберт Эйнштейн – фотонами. Оба этих названия прижились и употребляются до сих пор.
В итоге сложилась удивительная ситуация – сосуществование двух серьезных научных теорий, каждая из которых объясняла одни свойства света, но не могла объяснить другие. Вместе же эти две теории полностью дополняли друг друга. Только что мы рассмотрели ряд явлений, где свет ведет себя как поток частиц. Но явление интерференции и дифракции могут быть объяснены только с позиции волновой теории. Что же такое свет? В. Брегг писал: «неужели мы должны считать свет состоящим из корпускулов в понедельник, вторник и среду, когда проводим опыты с фотоэффектом и эффектом Комптона, и представлять себе его волнами в четверг, пятницу и субботу, когда работаем с явлениями дифракции и интерференции?» Выход из этой ситуации был найден следующий. Во-первых, электромагнитное излучение и его разновидность свет – это более сложный объект нашего мира, чем волна или корпускула. Во-вторых, нужна синтетезированная теория, объединяющая в себе и волновую, и корпускулярную теории. Она была создана и получила название квантовой физики.Очень важно, что квантовая физика не отвергает ни корпускулярную, ни волновую теории. Каждая из них имеет свои преимущества и свой, достаточно развитый математический аппарат.
Свет – диалектическое единство противоположных свойств: он одновременно обладает свойствами непрерывных электромагнитных волн и дискретных фотонов.
При уменьшении длины волны все явственнее проявляются корпускулярные свойства. Волновые свойства коротковолнового излучения проявляются слабо (например, рентгеновское излучение). Наоборот, у длинноволнового (инфракрасного) излучения квантовые свойства проявляются слабо.
Взаимосвязь между корпускулярными и волновыми свойствами света находит простое толкование при статистическом подходе к распространению света.
Взаимодействие фотонов с веществом (например, при прохождении света через дифракционную решетку) приводит к перераспределению фотонов в пространстве и возникновению дифракционной картины на экране. Очевидно, что освещенность в различных точках экрана прямо пропорциональна вероятности попадания фотонов в эти точки экрана. Но, с другой стороны, из волновых представлений видно, что освещенность пропорциональна интенсивности света J, а та, в свою очередь, пропорциональна квадрату амплитуды А2. Отсюда вывод: квадрат амплитуды световой волны в какой-либо точке есть мера вероятности попадания фотонов в эту точку.

77) ФОРМУЛА де БРОЙЛЯ И КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ
Фотоны проявляют двойственные свойства: в одних случаях ведут себя как частицы, а в других – как волны. Однако свойства частицы и волны несовместимы в головах современных ученых. Частица локализована в пространстве, а волна не занимает определенного пространственного положения. Поэтому возник термин: «корпускулярно-волновой дуализм» смысл которого так и остался непонятым. Луи де Бройль высказал смелое предположение, что корпускулярно-волновым дуализмом обладают все микрочастицы, что и подтвердилось экспериментально, они подчиняются формуле:
l=h/mV (1), где l - длина волны частицы, h – постоянная Планка, m – масса частицы, V – скорость ее движения.
Здесь нужно отметить нечестный прием официальной физики, которым она часто пользуется для маскировки собственных противоречий. В формуле (1) под постоянной Планка h имеется в виду вполне определенное численное значение, зависящее только от выбора системы единиц измерения, но не зависящее от конкретного физического объекта. Чтобы вывести это мошенничество на чистую воду, подставим в (1) постоянную Планка в другом виде: =h/2p:
l=2p/mV (2), но l/2p=r, где r – радиус винтовой траектории, тогда (2) превращается в определение момента импульса частицы:
=mVr (3). Но по представлениям официальной физики у «бозонов» целое или нулевое, а у «фермионов» - полуцелое, хотя те и другие подчиняются формуле (1) де Бройля, т.е. фактически соответствуют формуле (3). Следовательно ни «бозонов», ни «фермионов» не существует в природе. Они существуют только в головах теоретиков.
Еще одна грубая ошибка официальной физики состоит в том, что в знаменатель (1) подставляют огромную массу макротел, получают умопомрачительно малую «длину волны» этих тел и этим «подтверждают» правильность (1). Но извольте тогда и в числитель подставлять огромный момент импульса макротел, тогда получите «длину волны» космических масштабов.
Новая физика пошла дальше де Бройля и утверждает корпускулярно-волновой дуализм для любых свободных тел, в том числе и для макротел. Для них, аналогично формуле де Бройля (1), можно записать:
l=H/mv (4), где H – аналог постоянной Планка для макротел (очевидно, что обе постоянные Планка h и нельзя считать постоянными, т.к. момент импульса частицы может быть изменен).
Примем:
H/2p=L (5), тогда (4) можно переписать в виде:
l=2pL/mV (6), где L=mVr – момент импульса макротела на винтовой траектории или на стационарной орбите. Из (6) видно, что «длина волны» Земли равна длине окружности ее орбиты. Если Землю удалить от Солнца на периферию Солнечной системы, то в результате действия закона сохранения момента импульса, если ее скорость там окажется 1 км/сек (вместо 30 км/сек), то радиус орбиты и «длина волны» Земли увеличатся в 30 раз.
ПОЛЕВАЯ ПРИРОДА МАТЕРИИ(Волновая теория)
Поле - основа всей материи
«По современным представлениям, квантовое поле является наиболее фундаментальной и универсальной формой материи, лежащей в основе всех ее конкретных проявлений.»
Физическая энциклопедия. КВАНТОВАЯ ТЕОРИЯ ПОЛЯ.
«Принято считать, что масса элементарной частицы определяется полями, которые с ней связаны.»
Физический энциклопедический словарь. МАССА.
Т.е. весомая (вещественная) материя или составляющие ее элементарные частицы представляют овеществленную форму полевой материи - возбужденные состояния поля.
Волновая теория строения элементарных частиц является обобщением и последовательным развитием представлений о единстве природы вещества и поля, поэтому, как основа для рассмотрения этих вопросов, в тексте приводятся цитаты, которые по теме связаны с полевой природой материи. При этом предпочтение отдается материалистическим представлениям, а не метафизическим концепциям и интерпретациям, построенным на математическом формализме.
«... элементарные частицы материи по своей природе представляют собой не что иное, как сгущения электромагнитного поля,...»
А.Эйнштейн. Собрание научных трудов. М.: Наука. 1965. Т.1. С.689.
«... согласно последовательной теории поля весомую материю или составляющие ее элементарные частицы также следовало бы рассматривать как особого рода "поля", или особые "состояния пространства". Однако приходится признать, что при современном состоянии физики такая идея преждевременна, так как до сих пор все направленные к этой цели усилия физиков-теоретиков терпели провал. Таким образом, теперь мы фактически вынуждены различать "материю" и "поля", хотя и можем надеяться на то, что грядущие поколения преодолеют это дуалистическое представление и заменят его единым понятием, как это тщетно пыталась сделать теория поля наших дней.»
А.Эйнштейн. Собрание научных трудов. М.:Наука. 1966. Т.2. С.154.
Т.е. элементарные частицы, согласно последовательной теории поля, представляют особые состояния полевого пространства (состояние поля с наименьшей энергией называется вакуумом).
С современной точки зрения частицы материи - это квантованные волновые образования, возбужденные состояния квантового поля, т.е. последовательное рассмотрение строения элементарных частиц надо проводить, исходя из анализа возмущений поля, представляющих возбужденные состояния. Поэтому изложение волновой теории строения элементарных частиц начинается с рассмотрения основ полевой природы материи, анализа свойств дискретных полевых потоков, возмущений поля и протекающих в них процессов.
«С квантовой точки зрения элементарные возбуждения электромагнитного поля обладают всеми свойствами частиц.»

78) Соотношение неопределенности Гейзенберга представляется как одно из основных, фундаментальных положений квантовой механики.
Приводим характеристику, данную этому соотношению Л. Д. Ландау:
“Открытие принципа неопределенности показало, что человек в процессе познания природы может оторваться от своего воображения, он может открыть и осознать даже то, что ему не под силу представить” [1].
Точка зрения Ландау отражает распространенное мнение о соотношении неопределенности Гейзенберга. Рассмотрим положения, в основном, сформулированные авторами квантовой механики, связанными с изложением и трактовкой этого соотношения, которые могут оправдать приведенную характеристику.
1. “Классическая физика как раз и кончается в том месте, где нельзя уже отказаться от учета влияния наблюдателя на исследуемые процессы” [2]. “Невозможность отдалить самостоятельное поведение от их взаимодействия с измерительными приборами, предназначенных для изучения условий протекания явления, влечет за собой неоднозначность в приписывании обычных атрибутов атомным явлениям. Это обстоятельство вызывает необходимость пересмотра нашего отношения к проблеме физического объяснения” [3].
Данный фактор, в действительности, имеет место и в процессе обычных измерений, описываемых с помощью классической механики. Но влияние измерительного прибора и методики измерения либо учитывается и вводится поправка, либо результат измерений фигурирует как условный, т. е. оговаривается методика. Во всяком случае, этот фактор достаточно очевидный и не выглядит парадоксальным.
2. “Специфическая неточность, обусловленная соотношением неопределенности, в классической физике отсутствует” [4].
“В квантовой механике мы встречаемся с парадоксальной ситуацией — наблюдаемые события повинуются закону случая… Сегодня порядок идей обратный [по сравнению с “предвзятыми идеями о причинности”]: случайность стала первичным понятием” [5,6]. “С точки зрения квантовой теории нет никакой причины, по которой [например] распались имменно эти ядра, они распались “просто так”, спонтанно. Квантовая теория предсказывает лишь вероятность распада ядер” [7].
В данном случае отрицается наличие причины происходящих явлений. Это часто используемый в квантовой механике способ “решения научных задач”: проблема “закрывается” путем провозглашения соответствующего “закона” или “принципа”. Для Борна “детерминизм” являлся ярлыком, характеризующим неприятие “современной” науки [6]. Его совершенно не устраивала и “компромиссная” теория “скрытых переменных”.
В основе мистического миропонимания лежит аналогичное восприятие необъяснимого: подразумевается, что феномен, недоступный нашему пониманию, находится вне сферы возможности его объяснения.
Следует отметить, что не все классики квантовой механики придерживались этой теории, в частности, против нее решительно выступал Планк: “eсли подобный шаг оказался бы действительно необходимым, то тем самым цель физического исследования была бы значительно отброшена назад, что нанесло бы значительный ущерб, значение которого нетрудно оценить” [8]. Тем не менее, подобное толкование “принципа неопределенности” вошло в ортодоксальную науку.
3. Соотношение неопределенности ряд авторов рассматривал как отражение волновых свойств частиц — следствие корпускулярно-волнового дуализма. “Соотношения неопределенности Гейзенберга непосредственно вытекают из положения, что элементами новой картины мира являются не материальные частицы, а простейшие периодические волны материи” [9]. “Соотношения неопределенности следуют из способа которым связываются с помощью постоянной h корпускулярная и волновая сторона единых объектов вещества и излучения” [9].
Однако эта точка зрения не является обоснованной, о чем, в частности, свидетельствует вывод соотношения Гейзенбергом без “непосредственного обращения к волновой картине с помощью математической схемы квантовой теории” [9].
4. Соотношение неопределенности Гейзенберга показывает, что “между точностью, с которой одновременно может быть установлено положение частицы, и точностью ее импульса существует определенное соотношение” [2]:
q p ≥ h, (1)
где — среднеквадратичное отклонение. Нетрадиционное обозначение в формуле вводится для того, чтобы подчеркнуть отличие от единичного отклонения, которое часто обозначается символом D, что в отдельных случаях вызывает неверное толкование формулы.
О неприятии данного соотношения в период становления квантовой теории свидетельствуют дискуссии между Эйнштейном и Бором и, в частности, т. н. “парадокс Эйнштейна – Подольского – Розена”, в котором предполагается “мысленное” одновременное измерение импульса и координаты у двух частиц – “двойников” [3, 7,9,10].
Характерная деталь: анализ приведенного выражения проводится так, как будто это эмпирическая формула, а не соотношение, полученное аналитическим путем. В результате трактовка соотношения оказывается не связанной с предпосылками и условностями, которые подразумевались при его выводе, и это является одной из причин тех парадоксов, которые связываются с данным соотношением. Конкретно, эти противоречия отметим в заключении нашего анализа.
Приводим относительно простой вывод соотношения, делая упор на исходные постулаты и условности.
1. В основе соотношения лежит формула Планка, отражающая положение о квантовании “действия”:
E = nh
(E —энергия фотона, n — частота электромагнитной волны)
или ее следствия:
(p — импульс, l — длина волны).
Приращение “действия”, соответствующее h,
DSh = p Dq
(Dq — приращение координаты)
или при одновременном изменении p и q [11]
DSh = Dp Dq.(2)
2. Отметим, что проявление импульса невозможно без перемещения, а проявление энергии — вне времени. Под “проявлением” подразумевается регистрация путем взаимодействия объекта с наблюдателем, с измерительным прибором. Это условие справедливо и в классической механике.
3. В случае использования соотношения неопределенности, а возможно и в общем случае, измеряется “действие”, а не его компоненты — импульс, координаты, энергию, время.
Знаменательно — в действии объединены три основополагающие понятия: сила, длина, время. Измерительный же прибор “отградуирован”, соответственно, на импульс, координаты, энергию и время.
4. Неопределенность — это принципиальная невозможность определить величину параметра, а не результат влияния помех или ошибки измерения, подчиненных вероятностным законам, если их точное воздействие неизвестно.
Неопределенность, которую нельзя устранить, имеет место и в классической механике, она просто объясняется и легко воспринимается. Это случай, когда ограничена разрешающая способность конкретного измерительного инструмента: слишком велика при измерении “цена деления”, т. е. измерение осуществляется с помощью определенного шаблона, а требуется точность более высокая, чем та, что обеспечивается размерами или другими параметрами шаблона. Ни у кого, например, не вызывает удивления, что величина разрешения, достигаемого микроскопом, ограничена длиной волны в луче освещения. Эта неопределенность не связана с нашим незнанием причины погрешности, тем более, что этой причины не существует — у нас нет методики или инструмента для более точного определения измеряемого параметра.
5. В соотношении неопределенность рассматривается как фактор, вызывающий ошибку. Следовательно, формально предполагается стремление получить большую точность, чем та, которая может обеспечить дискретная величина кванта действия.
Если проводим измерение длины R линейкой с ценой деления r, то мы можем сказать, что гарантированная точность — ± r и абсолютная ошибка измерения — D R = r. Но если мы из результата измерения хотим оценить возможное значение R с большей точностью, чем допускается цена деления, то D R ≤ r.
Из примеров использования соотношения, которые приводит Гейзенберг [9], следует, что имеется в виду первый вариант, то есть под неопределенностью в соотношении понимается — невозможность определения значения параметра, связанная с его оценкой исключительно с той точностью, которая обеспечивается методикой.
Приведенные положения исходя из формулы (2) позволяют выразить, в соответствии с п. 5, ошибку измерения действия
DS ≥ Dp Dq ≥ DSh = h (3)
DS ≥ DE Dt ≥ DSh = h (4)
Если соотношению удовлетворяют каждое конкретное измерение, то ему соответствует результат при их статистической обработке — (1), и его разновидность — соотношение неопределенности Бора:
E t ≥ h. (5)
Выражения (1) и (5), включающими усредненную погрешность, не являются основными — они приводятся в связи с традиционным представлениям соотношения. Значительно большее теоретическое и практическое содержание заключено в формулах (3), (4).
Традиционное выражение соотношения связано с укоренившимся взглядом на волновые свойства частиц, который представляется цепочкой: частица — волновой пакет — вероятностная интерпретация волновой функции, по которой рассматривается только вероятность характеристик частицы. Даже тогда, когда Гейзенберг выводит соотношение “без обращения к волновой картине”, он рассматривает среднеквадратичное отклонение p и q, при этом приписывает этим величинам гауссовское распределение вероятности [5], хотя, как указывалось, основной фактор, влияющий на погрешность, не связан со случайными воздействиями, да их и может не существовать. Использование волновой функции [12,13], даже, считая ее абстракцией, затмевает физическую сущность соотношения.

ВОЛНОВАЯ ФУНКЦИЯ, в КВАНТОВОЙ МЕХАНИКЕ - функция, позволяющая найти вероятность того, что квантовая система находится в некотором состоянии s в момент времени t. Обычно пишется: (s) или (s, t). Волновая функция используется в уравнении ШРЕДИНГЕРА.

Физический смысл волновой функции:
Волновая функция зависит от координат (или обобщённых координат) системы и, в общем случае, от времени, и формируется таким образом, чтобы квадрат её модуля представлял собой плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами в момент времени:
Тогда в заданном квантовом состоянии системы, описываемом волновой функцией, можно рассчитать вероятность того, что частица будет обнаружена в любой области пространства конечного объема:
Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор величин определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока и др.
Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.

Свойства волновой функции:
Отметим свойства волновой функции в частном случае трёхмерного пространства в декартовых координатах. В этом случае зависит от трёх переменных и имеет следующие свойства (справедливо только для таких волновых функций, которые являются решением уравнения Шредингера):
1.Правило нормировки:
Правило выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией во всем пространстве равна единице.
2.Импульс частицы в каждом из направлений пропорционален первой производной волновой функции, делённой на саму волновую функцию, а именно
где — проекции импульсов на соответствующие оси координат, — мнимая единица, — постоянная Планка.
3.Кинетическая энергия частицы пропорциональна второй производной, или кривизне волновой функции, деленной на эту волновую функцию

79). Уравнение Шредингера для стационарных состояний
В развитие идеи де Бройля о волновых свойствах частиц Шредингер в 1926 г. получил уравнение

где m - масса частицы, i=корень из -1 - мнимая единица, U - потенциальная энергия частицы, D - оператор Лапласа.
Решение уравнения Шредингера позволяет найти волновую функцию Y(x, y, z, t) частицы, которая описывает микросостояние частицы и ее волновые свойства.
Если поле внешних сил постоянно во времени (т.е. стационарно), то U не зависит явно от t. В этом случае решение уравнения (20) распадается на два множителя
Y(x, y, z, t) =y(x, y, z) exp[-i(E/h)t] (21)
где E/h=w.

В стационарном случае уравнение Шредингера имеет вид

(22)

где Е, U - полная и потенциальная энергия, m - масса частицы.
Следует заметить, что исторически название "волновой функции" возникло в связи с тем, что уравнение (20) или (22), определяющее эту функцию, относится к виду волновых уравнений.

Свободной называют частицу, на которую не действуют силы, т.е.F(x)= -дельта U/д.X=0. Cледовательно, U(x)=const и ее можно принять равной нулю. Таким образом, в случае свободного движения частицы, ее полная энергия совпадает с кинетической, а скорость. Направим ось Х вдоль вектора. Тогда (22) можно записать в виде

. (23)
Прямой подстановкой можно убедится, что частным решением этого уравнения является функция y(х)=Аexp(ikx), где А=сonst, k=const c собственным значением энергии

E= .(24)

C учетом (21) волновая функция

Y(х)=Аexp(-iwt+ ikx)= Аexp[-(i/h)(Еt- р_xх)]. (25)

здесь w=Е/h, k=р_x/h

Функция (25) представляет собой плоскую монохроматическую волну де Бройля.
Из (24) следует, что зависимость энергии от импульса

Е=h²k²/(2m)=Р_x²/(2m)=mv²/2 (26)
оказывается обычной для нерелятивиских частиц. Следовательно, энергия свободной частицы может принимать любые значения, т.е. ее энергетический спектр является непрерывным.
Плотность вероятности обнаружить частицу в данной точке пространства
|y| 2=yy*=A2,т.е. все положения свободной частицы в пространстве являются равновероятными.
Электроны в потенциальном ящике:
Положим, что в таком ящике находится один электрон (или любая другая частица), и по­пробуем решить вопрос о ха­рактере его движения. Мы ре­шаем простейшую одномерную задачу и полагаем, что электрон движется лишь вдоль оси х. Ес­ли бы к электрону были приме­нимы законы механики Ньютона, то такой электрон двигался бы непрерывно сначала в одну сто­рону ящика, упруго отражал­ся бы от стенки, затем двигался бы в обратную сторону и т. д.
Иначе быть не может с точки зрения механики Ньютона, поскольку при U—0 кинетическая энергия mv2!2 будет постоянной. Таким образом, по поводу возможных движений в потенциальном ящике механика «обычной» частицы приводит к следующим заключениям. В ящике возможно движение с любой кинетической энергией mv2!2; частица может также покоиться в ящике. Для каждой данной энер­гии движение будет равномерным и будет происходить то в одну, то в другую сторону, причем в конце дозволенного интервала скорость меняется скачком по направлению.
Посмотрим теперь, какой ответ о движении электрона в таком ящике даст квантовая механика.
Поведение электрона мы должны характеризовать функцией -ф, квадрат которой укажет вероятность нахождения электрона в какой- либо точке дозволенного отрезка. Так как внутри ящика U=0, то уравнение Шредингера упрощается и записывается в виде

0, где К-. h

d2\, 4л2, Т.-Г + ТГ'Г

dx2 г Я* • у^Ш

Этому уравнению удовлетворяют синус и косинус от аргумента. Если ящик ограничен координатами х=0 и х*=а, то при этих
значениях i|j=0 (за стенки электрон не проникает). Поэтому cos 2я y не годится в качестве решения уравнения (cos2rcy= 1 при л:=0). Значит,
if) = A sin -J- х.
Но длина волны к не может быть любой, так как i|?=0 при х~а. Значит, должно выполняться равенство

Y а = (п+ 1)я,

или
где я = 0, 1, 2,...
Итак, длина волны может принять значения 2а, а, ^, ~,...
Мы видим, что "ф-функция представляет собой амплитуду стоячей волны (ср. стр. 116) и вся рассмотренная задача имеет фор­мально много общего с задачей колебания стержня или струны. Но если длина волны к имеет дискретный ряд значений, то энергия ^ микрочастицы уже не может быть любой, а равна
целое число п называется квантовым числом.
Таким образом, уравнение Шредингера приводит к квантова­нию энергии. Микрочастица в потенциальном ящике имеет ряд ди­скретных уровней энергии. Самый низкий энергетический уровень
имеет место при п—0. Энергия равна. Это — нулевая энер­гия частицы, находящейся в потенциальном ящике.
Наличие нулевой энергии является интересной особенностью микрочастиц. У «обычных» частиц низшей энергией является нуле­вое значение. У микрочастиц ни при каких условиях не достигается прекращение движения. При абсолютном нуле температуры микро­частица обладает определенной нулевой энергией, существенно различной в зависимости от характера поля сил, в котором находится частица.
Пример. Пусть а=\ А (характерная для атомной области величина). Тогда нулевая энергия электрона в потенциальном ящике будет
/i2 fi.10-27}2
Ш-'М10-«Г0'6,10"10ЭРГ=37 ЭВ'
Пусть а— 1 см (свободный электрон в куске металла). Тогда^0—0,6- Ю-26 эрг= =37.10-16эВ.
Находясь на данном энергетическом уровне, электрон имеет скорость, которую можно вычислить из длины волны: v=h/mk. Однако движение электрона уже нельзя описывать уравнениями
классическом механики, и невозможно указать, где находится элек­трон в тот или иной момент времени. Зато можно найти значение^2, т. е. плотность вероятности нахождения электрона в том или ином месте пространства, по уравнению
ур* = A2 sin2 ~ х - A2 sin2 - (п + 1) х.
A CL
Характерным обстоятельством является следующее: каждому энергетическому уровню соответствует своя (того же номера п) волновая функция (собственная функция).
f(x)

A AAAI

На рис. 211 показана г|>функция и ее квадрат для четырех пер­вых энергетических уровней электрона, находящегося в потенциаль­ном ящике. Ква

Поделиться:

Воспользуйтесь поиском по сайту: