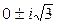| № п/п
| Задание
| Ответ
|
|
| Вычислите  . Результат представьте в алгебраической форме. Решение: . Результат представьте в алгебраической форме. Решение:
 . .
| 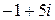 . .
|
|
| Вычислите  . Результат представьте в алгебраической форме.
Решение: . Результат представьте в алгебраической форме.
Решение:
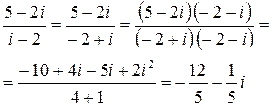
| 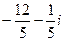
|
|
| Вычислите  . Результат представьте в алгебраической форме. Решение: . Результат представьте в алгебраической форме. Решение:
 . .
| 
|
|
| Найдите  и и  для числа для числа 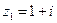 .
Решение: .
Решение:
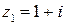 , , 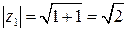 , ,  . .
| 
|
|
| Запишите число 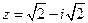 в различных формах. Дайте геометрическую интерпретацию.
Решение:
Алгебраическая форма: в различных формах. Дайте геометрическую интерпретацию.
Решение:
Алгебраическая форма: 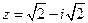 ;
тригонометрическая форма: ;
тригонометрическая форма: 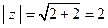 ; ;  ,
откуда ,
откуда 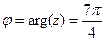 , ,
 ;
показательная форма: ;
показательная форма:  . .
|  , , 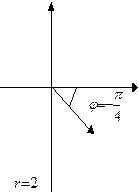  . .
|
|
| Запишите комплексные числа
1)  ; 2) ; 2)  ; 3) ; 3) 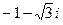 в тригонометрической и показательной форме:
Решение:
1)
в тригонометрической и показательной форме:
Решение:
1) 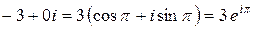 ;
2) ;
2) 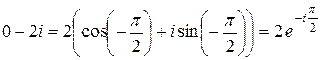 ;
3) ;
3)  . .
|
|
|
| Найдите  , если , если  .
Решение: .
Решение:
 ( ( расположено в IV квадранте).
Тогда расположено в IV квадранте).
Тогда 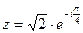 . .
  . .
|  . .
|
|
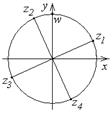
| Вычислите и изобразите на комплексной плоскости  .
Решение:
Запишем число .
Решение:
Запишем число  в показательной форме: в показательной форме: 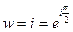 ; ;
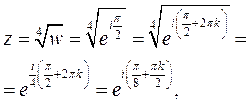 . .
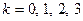 . .
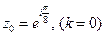 , , 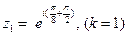 , ,  , , 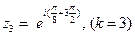 . .
 получен из корня получен из корня  поворотом на поворотом на 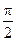 против часовой стрелки, против часовой стрелки, 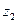 из из 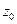 поворотом на поворотом на 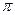 и т.д. и т.д.
| 
|
|
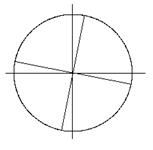
| Найдите все значения  и постройте их на комплексной плоскости.
Решение:
Представим число и постройте их на комплексной плоскости.
Решение:
Представим число 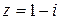 в тригонометрической форме. в тригонометрической форме.
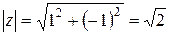 , ,  . .
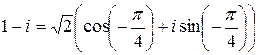 . .
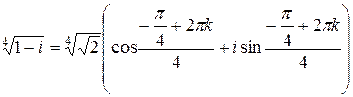 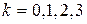 . .
 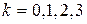 .
При .
При 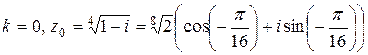 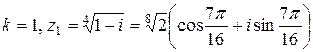 , ,
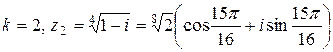 , ,
 . .
| 
|
|
| Найдите все значения корня  .
Решение: .
Решение:
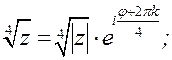 где где  . .  , ,  , ,  , ,
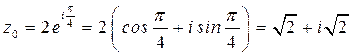 , и т.д. , и т.д.
| 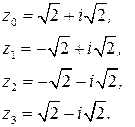
|
|
| Вычислите, найдите модуль, аргумент и постройте на комплексной
плоскости число 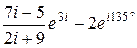 .
Решение:
1) .
Решение:
1)
 , ,
 .
Для правильного отыскания аргумента рекомендуется изобразить это число на комплексной плоскости. .
Для правильного отыскания аргумента рекомендуется изобразить это число на комплексной плоскости.
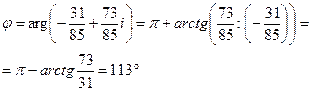 ; ;  ;
2) ;
2) 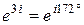 (3 радиана (3 радиана  , так как 1 радиан , так как 1 радиан  );
3) );
3) 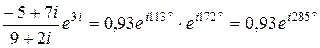 ;
4) ;
4) 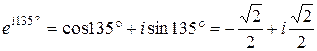 ;
5) ;
5) 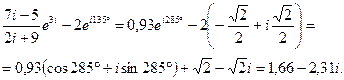 Вычислим модуль и аргумент полученного числа:
Вычислим модуль и аргумент полученного числа:  , ,  . .
  . .
| 

|
|
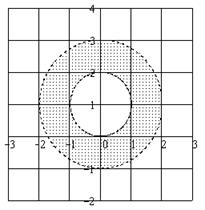
| Дайте геометрическое описание множества всех точек комплексной плоскости, удовлетворяющих условиям: 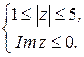 Решение: Запишем
Решение: Запишем  в алгебраической форме в алгебраической форме  , тогда из условия: , тогда из условия: 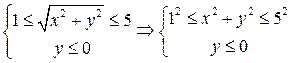 .
Искомое множество – нижняя половина кольца с внутренним радиусом .
Искомое множество – нижняя половина кольца с внутренним радиусом 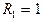 и внешним и внешним  . .
| 
|
|
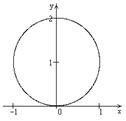
| Найдите множество точек комплексной плоскости, удовлетворяющих уравнению  Решение:
Решение:
 , ,
 .
Искомое множество состоит из точек окружности единичного радиуса, центр которой имеет координаты .
Искомое множество состоит из точек окружности единичного радиуса, центр которой имеет координаты 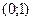 . .
| 
|
|
| Какие геометрические образы определяются условиями 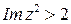 ? ?
| 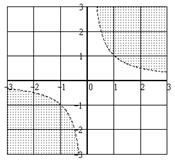 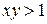 . (см. рисунок). . (см. рисунок).
|
|
| Какие геометрические образы определяются условиями 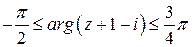 ? ?
|  . .  (см. рисунок). (см. рисунок).
|
|
| Какие геометрические образы определяются условиями 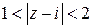 ? ?
|  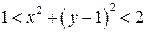 . (см. рисунок). . (см. рисунок).
|
|
| Дайте геометрическое описание множеств всех точек комплексной плоскости, удовлетворяющих следующим условиям: 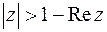 . .
|  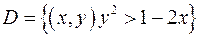
|
| Многочлены в комплексной области
|
| № п/п
| Задание
| Ответ
|
|
| Проверьте, что  является корнем многочлена является корнем многочлена  и найдите другие корни многочлена.
Решение:
Так как и найдите другие корни многочлена.
Решение:
Так как  , то , то  является корнем многочлена является корнем многочлена  и многочлен и многочлен  делится на делится на  без остатка. без остатка. 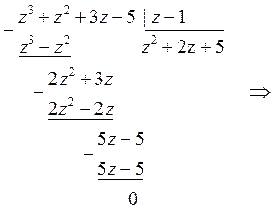  Для отыскания других корней многочлена решим уравнение
Для отыскания других корней многочлена решим уравнение 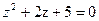 : :  Итак, многочлен Итак, многочлен 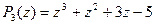 имеет один действительный корень имеет один действительный корень  и два комплексно-сопряженных корня и два комплексно-сопряженных корня 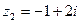 , , 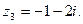
| 
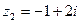
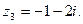
|
|
| Разложите на множители 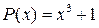 .
Решение: .
Решение:
 , , 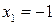 -действительный корень, у квадратного трехчлена действительных корней нет. Найдем пару комплексно-сопряженных корней: -действительный корень, у квадратного трехчлена действительных корней нет. Найдем пару комплексно-сопряженных корней: 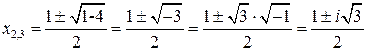 , ,  . .
| 
|
|
| Решите уравнение 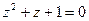 .
Используя формулу для решения квадратного уравнения и полагая .
Используя формулу для решения квадратного уравнения и полагая  , получим: , получим: 
| 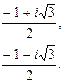
|
|
| Решите уравнение  .
Решение:
Введём подстановку .
Решение:
Введём подстановку  . Получим квадратное уравнение . Получим квадратное уравнение 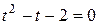 . По теореме Виета корни квадратного уравнения . По теореме Виета корни квадратного уравнения 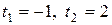 , и исходное уравнение распадается на два более простых уравнения , и исходное уравнение распадается на два более простых уравнения  и и 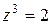 , решения которых и дадут в совокупности все решения данного уравнения. Если , решения которых и дадут в совокупности все решения данного уравнения. Если  , то , то  .
В тригонометрической форме .
В тригонометрической форме  , поэтому , поэтому  , ,  или или 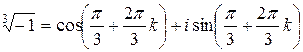 , ,  .
При .
При 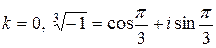 .
При .
При 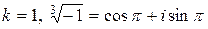 .
При .
При  . Если . Если 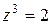 , то , то  .
В тригонометрической форме .
В тригонометрической форме  , поэтому , поэтому  , ,  .
При .
При 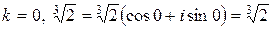 .
При .
При 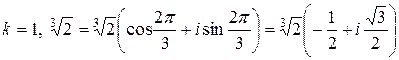 .
При .
При 

|
|
|
| Решите уравнение  .
По формуле корней квадратного уравнения .
По формуле корней квадратного уравнения
 .
Число, стоящее под знаком квадратного корня, можно было бы записать в показательной форме, а затем по известному правилу извлечь из него корень. Однако можно поступить иначе. Положим .
Число, стоящее под знаком квадратного корня, можно было бы записать в показательной форме, а затем по известному правилу извлечь из него корень. Однако можно поступить иначе. Положим  Возводим обе части в квадрат и находим
Возводим обе части в квадрат и находим  , откуда , откуда  ; ;  .
Эта система имеет решения: .
Эта система имеет решения: 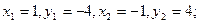 поэтому поэтому

| 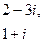
|
| | | | | | | | |

 . Результат представьте в алгебраической форме. Решение:
. Результат представьте в алгебраической форме. Решение:
 .
.
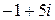 .
.
 . Результат представьте в алгебраической форме.
Решение:
. Результат представьте в алгебраической форме.
Решение:
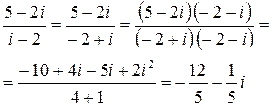
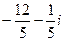
 . Результат представьте в алгебраической форме. Решение:
. Результат представьте в алгебраической форме. Решение:
 .
.

 и
и  для числа
для числа 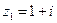 .
Решение:
.
Решение:
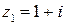 ,
, 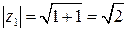 ,
,  .
.

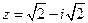 в различных формах. Дайте геометрическую интерпретацию.
Решение:
Алгебраическая форма:
в различных формах. Дайте геометрическую интерпретацию.
Решение:
Алгебраическая форма: 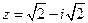 ;
тригонометрическая форма:
;
тригонометрическая форма: 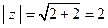 ;
;  ,
откуда
,
откуда 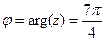 ,
,
 ;
показательная форма:
;
показательная форма:  .
.
 ,
, 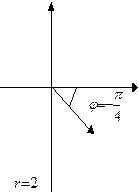
 .
.
 ; 2)
; 2)  ; 3)
; 3) 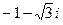 в тригонометрической и показательной форме:
Решение:
1)
в тригонометрической и показательной форме:
Решение:
1) 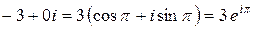 ;
2)
;
2) 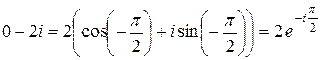 ;
3)
;
3)  .
.
 , если
, если  .
Решение:
.
Решение:
 (
( расположено в IV квадранте).
Тогда
расположено в IV квадранте).
Тогда 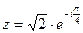 .
.

 .
.
 .
.
 .
Решение:
Запишем число
.
Решение:
Запишем число  в показательной форме:
в показательной форме: 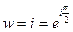 ;
;
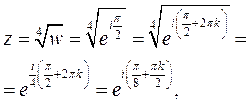 .
.
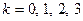 .
.
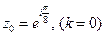 ,
, 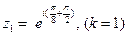 ,
,  ,
, 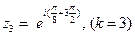 .
.
 получен из корня
получен из корня  поворотом на
поворотом на 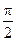 против часовой стрелки,
против часовой стрелки, 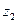 из
из 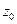 поворотом на
поворотом на 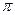 и т.д.
и т.д.

 и постройте их на комплексной плоскости.
Решение:
Представим число
и постройте их на комплексной плоскости.
Решение:
Представим число 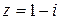 в тригонометрической форме.
в тригонометрической форме.
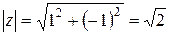 ,
,  .
.
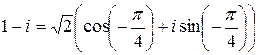 .
.
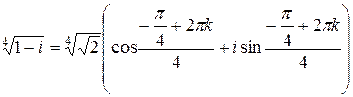
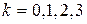 .
.

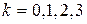 .
При
.
При 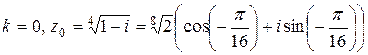
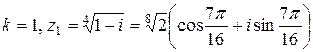 ,
,
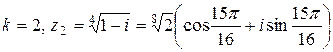 ,
,
 .
.

 .
Решение:
.
Решение:
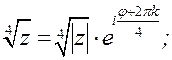 где
где  .
.  ,
,  ,
,  ,
,
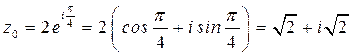 , и т.д.
, и т.д.
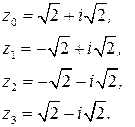
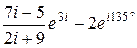 .
Решение:
1)
.
Решение:
1)
 ,
,
 .
Для правильного отыскания аргумента рекомендуется изобразить это число на комплексной плоскости.
.
Для правильного отыскания аргумента рекомендуется изобразить это число на комплексной плоскости.
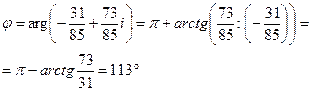 ;
;  ;
2)
;
2) 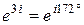 (3 радиана
(3 радиана  , так как 1 радиан
, так как 1 радиан  );
3)
);
3) 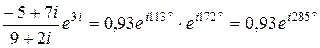 ;
4)
;
4) 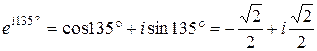 ;
5)
;
5) 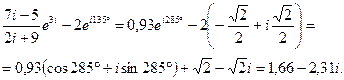 Вычислим модуль и аргумент полученного числа:
Вычислим модуль и аргумент полученного числа:  ,
,  .
.

 .
.


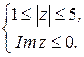 Решение: Запишем
Решение: Запишем  в алгебраической форме
в алгебраической форме  , тогда из условия:
, тогда из условия: 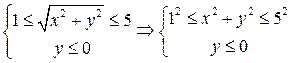 .
Искомое множество – нижняя половина кольца с внутренним радиусом
.
Искомое множество – нижняя половина кольца с внутренним радиусом 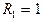 и внешним
и внешним  .
.

 Решение:
Решение:
 ,
,
 .
Искомое множество состоит из точек окружности единичного радиуса, центр которой имеет координаты
.
Искомое множество состоит из точек окружности единичного радиуса, центр которой имеет координаты 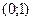 .
.

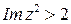 ?
?

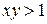 . (см. рисунок).
. (см. рисунок).
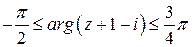 ?
?
 .
.  (см. рисунок).
(см. рисунок).
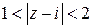 ?
?

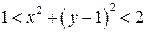 . (см. рисунок).
. (см. рисунок).
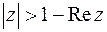 .
.

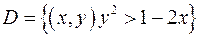
 является корнем многочлена
является корнем многочлена  и найдите другие корни многочлена.
Решение:
Так как
и найдите другие корни многочлена.
Решение:
Так как  , то
, то  является корнем многочлена
является корнем многочлена  и многочлен
и многочлен  делится на
делится на  без остатка.
без остатка. 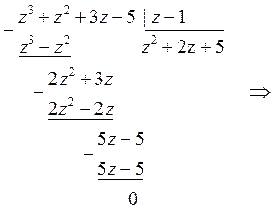
 Для отыскания других корней многочлена решим уравнение
Для отыскания других корней многочлена решим уравнение 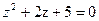 :
:  Итак, многочлен
Итак, многочлен 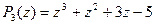 имеет один действительный корень
имеет один действительный корень  и два комплексно-сопряженных корня
и два комплексно-сопряженных корня 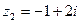 ,
, 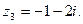

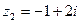
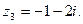
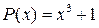 .
Решение:
.
Решение:
 ,
, 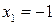 -действительный корень, у квадратного трехчлена действительных корней нет. Найдем пару комплексно-сопряженных корней:
-действительный корень, у квадратного трехчлена действительных корней нет. Найдем пару комплексно-сопряженных корней: 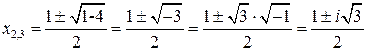 ,
,  .
.

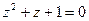 .
Используя формулу для решения квадратного уравнения и полагая
.
Используя формулу для решения квадратного уравнения и полагая  , получим:
, получим: 
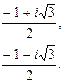
 .
Решение:
Введём подстановку
.
Решение:
Введём подстановку  . Получим квадратное уравнение
. Получим квадратное уравнение 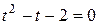 . По теореме Виета корни квадратного уравнения
. По теореме Виета корни квадратного уравнения 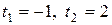 , и исходное уравнение распадается на два более простых уравнения
, и исходное уравнение распадается на два более простых уравнения  и
и 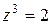 , решения которых и дадут в совокупности все решения данного уравнения. Если
, решения которых и дадут в совокупности все решения данного уравнения. Если  , то
, то  .
В тригонометрической форме
.
В тригонометрической форме  , поэтому
, поэтому  ,
,  или
или 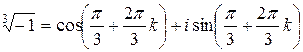 ,
,  .
При
.
При 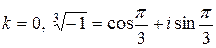 .
При
.
При 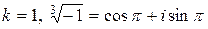 .
При
.
При  . Если
. Если 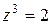 , то
, то  .
В тригонометрической форме
.
В тригонометрической форме  , поэтому
, поэтому  ,
,  .
При
.
При 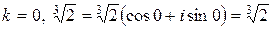 .
При
.
При 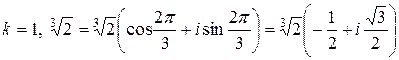 .
При
.
При 

 .
По формуле корней квадратного уравнения
.
По формуле корней квадратного уравнения
 .
Число, стоящее под знаком квадратного корня, можно было бы записать в показательной форме, а затем по известному правилу извлечь из него корень. Однако можно поступить иначе. Положим
.
Число, стоящее под знаком квадратного корня, можно было бы записать в показательной форме, а затем по известному правилу извлечь из него корень. Однако можно поступить иначе. Положим  Возводим обе части в квадрат и находим
Возводим обе части в квадрат и находим  , откуда
, откуда  ;
;  .
Эта система имеет решения:
.
Эта система имеет решения: 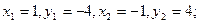 поэтому
поэтому

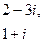
 . Результат представьте в алгебраической форме.
. Результат представьте в алгебраической форме. 
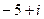
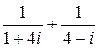 . Результат представьте в алгебраической форме.
. Результат представьте в алгебраической форме.

 ; 2)
; 2) 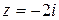 ; 3)
; 3)  .
.
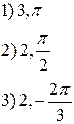
 .
.
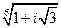 ; изобразите схематично значения корня на комплексной плоскости.
; изобразите схематично значения корня на комплексной плоскости.

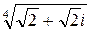 .
.
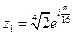 ,
, 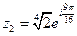 ,
,  ,
,  .
.
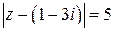 ?
?

 ?
?



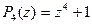 .
.
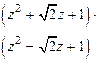
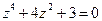 .
.