Понятие обусловленности системы

Глава 3. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

 

Прямые методы

Правило Крамера

Пусть дана система n линейных алгебраических уравнений с n неизвестными

 

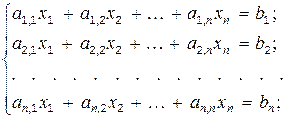(3.1)

 

или, в другой записи,

, (). (3.1¢)

 

Запишем (3.1) в векторно-матричной форме

 

(3.1¢¢)

где

 

, , .

 

 

Предположим, что существует обратная матрица . Умножая левую и правую части (3.1¢¢) на , получаем решение системы в виде

 

. (3.2)

 

Для вычисления можно использовать правило, известное из общего курса высшей математики:

 

, (3.3)

 

где матрица составлена из алгебраических дополнений элементов , - транспонированная матрица.

Подставляя (3.3) в (3.2), получаем следующую расчетную формулу

 

(3.4)

или

, (), (3.4¢)

 

где

 

 

- детерминант, получающийся из детерминанта заменой i -го столбца матрицы A столбцом свободных членов . Этот способ вычисления известен как правило Крамера.

Таким образом, решение системы (3.1) с n неизвестными сводится к вычислению (n + 1)-го определителя порядка n. При вычислении определителя порядка n число арифметических операций имеет порядок , и при вычисление детерминанта становится трудоемкой задачей.

 

 

Метод Гаусса

Алгоритм вычисления неизвестных состоит из двух частей. Первая часть алгоритма - приведение системы (3.1) к верхней треугольной форме (прямой ход). Вторая часть - решение преобразованной системы с помощью обратной подстановки (обратный ход).

Предположим, что в процессе приведения исходной системы уравнений к верхней треугольной форме не возникает деления на нуль. Для удобства рассуждений составим расширенную матрицу исходной системы уравнений:

 

 

, (3.5)

 

где , (). Строки этой матрицы соответствует уравнениям системы (3.1).

На первом шаге прямого хода алгоритма разделим первую строку на и вычтем новую строку с множителем из каждой i –й строки для . В результате указанных комбинаций со строками расширенная матрица (3.5) приобретает вид

 

, (3.6)

где

 

.

 

На втором шаге прямого хода алгоритма делим вторую строку матрицы (3.6) на , затем умножаем ее последовательно на и вычитаем из строк с номерами . В результате получаем

 

, (3.7)

где

 

.

 

На k –м шаге имеем

 

, (3.7)

где

 

.

 

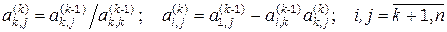Наконец, на n -м шаге получаем

 

, (3.8)

где

 

.

 

Теперь исходная система преобразована к виду

 

, (3.9)

 

где

, .

 

 

Все последовательно выражаются из (3.9):

(3.10)

 

После вычисления x ₁ обратный ход алгоритма заканчивается. Элементы , называются ведущими. Метод реализуем, если и только если ведущие элементы не равны нулю. Если это условие не выполняется, то применяется метод Гаусса с выбором главных элементов.

 

 

Схема Холецкого

Метод исключения Гаусса можно модифицировать следующим образом. Воспользуемся теоремой матричной алгебры, согласно которой любую квадратную матрицу можно представить произведением нижней и верхней треугольных матриц. Факторизация становится однозначной, если зафиксировать элементы на главной диагонали одной из матриц.

Положим

 

, (3.11)

где

 

, .

 

Формулы для вычисления элементов матриц C и B определяются из соотношения (3.11):

 

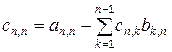. (3.12)

 

В этом случае , и решение получается в результате последовательного решения треугольной системы :

 

(3.13)

 

и треугольной системы :

 

(3.14)

 

Из систем (3.13) и (3.14) последовательно находим

 

(3.15)

и

(3.16)

 

Таким образом, формулы (3.12) представляют первую часть алгоритма, состоящего в факторизации матрицы исходной системы уравнений. Формулы (3.15), (3.16) представляют вторую часть алгоритма, где вычисляются неизвестные величины. Данный алгоритм носит название вычислительной схемы Холецкого. Частным случаем схемы Холецкого является метод квадратного корня, который разработан для решения систем линейных алгебраических уравнений с симметрической положительно определенной матрицей. Симметрическая матрица представляется в виде произведения двух треугольных матриц, транспонированных друг относительно друга: . Далее решение системы получается в результате последовательного решения двух систем с треугольными матрицами, и .

 

Метод итераций

 

Выполним преобразование исходной системы уравнений (3.1¢¢), не изменяющее ее решение:

 

. (3.17)

 

где H – невырожденная матрица. С учетом обозначений , 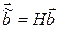система перепишется следующим образом:

 

. (3.18)

 

Систему (3.18) решаем методом последовательных приближений. Пусть - нулевое приближение. В качестве нулевого приближения можно выбрать вектор . Строим итерационный процесс:

 

(3.19)

 

Указанный метод называется методом простой итерации. Если последовательность имеет предел , то в силу = этот предел является решением системы (3.17) и, следовательно, решением системы (3.1¢¢).

Теорема о достаточном условии сходимости итерационного процесса (3.19) формулируется следующим образом.

 

Теорема 3.1. Достаточным условием сходимости итерационного процесса (3.19) независимо от начального приближения является условие

 

, (3.20)

 

где 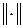- евклидова норма матрицы.

Понятие обусловленности системы

 

Говорят, что система линейных уравнений (3.1) плохо обусловлена, если малые изменения элементов матрицы коэффициентов или правых частей приводят к большим изменениям в решении.

Мерой обусловленности матрицы A естественно считать объем n -мерного параллелепипеда, построенного на единичных отрезках, коллинеарных строкам матрицы A:

 

, (3.21)

 

где . Если V (A) = 1, то матрица A идеально обусловлена. Если

V (A) << 1, то матрица A плохо обусловлена. Если V (A) = 0, то det(A) = 0 и матрица A вырождена. В двумерном случае объемом V является площадь ромба, изображенного на рисунке.

 

 

 

 

 

В качестве меры обусловленности используется также число

 

, (3.22)

 

называемое числом обусловленности. Число r может принимать значения в полуинтервале [1,µ). Чем больше r, тем хуже обусловлена матрица.

Плохая обусловленность - эффект вычислительный. Если матрица A вырождена, то det(A) = 0, не существует, r = ¥ и вопрос о плохой обусловленности не возникает. Но из малости det(A) не следует, что матрица A

плохо обусловлена. Например, матрица A = идеально обусловлена, поскольку , но .

Плохая обусловленность системы (3.1) устраняется увеличением вычислительной точности либо изменением входных данных. Признаком плохой обусловленности является det(A) << 1, но, как показывает приведенный выше пример, не всегда. Практическая проверка обусловленности состоит в проверке чувствительности решения к малым изменениям коэффициентов и , либо вычислении V или r.

Оценка относительной погрешности решения исходной системы в зависимости от относительных погрешностей коэффициентов задачи имеет вид:

 

, (3.23)

 

где - погрешность решения, , - погрешности коэффициентов задачи. Эта формула справедлива при условии . При формула (3.23) упрощается:

 

. (3.24)

 

 

Поделиться:

Воспользуйтесь поиском по сайту: