|
Постановка экспериментальной задачи
|
|
|
|
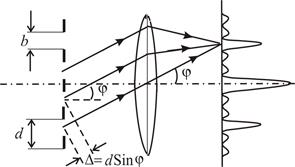
Рассмотрим подробнее процесс прохождения света через дифракционную решетку. Пусть дифракционная решетка (рис.1.) имеет N щелей шириной b, постоянная (период) решетки равна d.
Каждая из N щелей даст на экране картину, описываемую кривой дифракции от одной щели. Картины от всех щелей придутся на одно и то же место экрана. Если бы колебания световых волн, приходящие от различных щелей, были некогерентными, то картина на экране отличалась бы от картины, создаваемой одной щелью только тем, что все интенсивности возросли бы в N раз. Однако колебания являются когерентными, что приводит к необходимости учета интерференционных эффектов.
Чтобы определить амплитуду результирующего колебания, необходимо вычислить сумму N колебаний с одинаковой амплитудой А j и сдвинутых друг относительно друга по фазе на одну и ту же величину d.
| |||
| Рис.1 |
Расчет показывает, что искомая амплитуда равна:
 (1)
(1)
Следовательно, интенсивность окажется равной
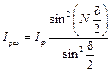 (2)
(2)
Из рисунка 1 видно, что разность хода D от эквивалентных точек соседних щелей D = d sinj, следовательно, разность фаз
d = 2 pD / l =  , (3)
, (3)
Подставляя значение d в формулу (2), можно получить
 (4)
(4)
Отношение квадратов синусов принимает значения N2 для направлений, удовлетворяющих условию
d sinj = ± k l, k = 0, 1, 2,... (5)
Лучи, идущие от отдельных щелей в этих направлениях, усиливают друг друга и интенсивность в соответствующей точке фокальной плоскости линзы, собирающей эти лучи, будет равна N 2 I j. Максимумы, получающиеся в таких точках, называются главными максимумами. Число k называется порядком главных максимумов. При k =0 угол j равен нулю. Наблюдается максимум нулевого порядка, располагающийся экспериментально в фокусе линзы. Ближайшие к нулевому максимумы возникают при k = ± 1 и называются максимумами первого порядка и т.д.
|
|
|
Между каждой смежной парой главных максимумов образуется (N - 1) вторичных минимумов, возникающих в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Условием этого будет
d sinj = ±  l (6)
l (6)
Здесь K ' может принимать все целочисленные значения кроме кратных N, при которых наблюдаются главные максимумы.
Между вторичными минимумами располагаются вторичные максимумы, число которых равно N - 2. Интенсивность вторичных максимумов не превышает 1/23 (4%) от интенсивности ближайшего главного максимума (см. рис.1).
Для полного расчета распределения интенсивности необходимо учесть и распределение интенсивности от одной щели I j. Оно является сомножителем результирующей интенсивности. Следовательно, интенсивности главных максимумов не будут одинаковыми (рис.2), а оказываются промодулированы кривой, описывающей распределение интенсивности от одной щели. При определенных соотношениях b и d возможен случай, когда отдельные главные максимумы не будут наблюдаться, если их положение совпадает с условием I j = 0.
На рис.2. приведено распределение интенсивности от 4 щелей (N = 4), для которых отношение d/b =3.
| |||
| Рис.2 |
Как видно из формулы (5), положение главных максимумов определяется постоянной решетки d и длиной волны l.
Для различных l максимумы образуются при различных значениях j, т.е. происходит разложение немонохроматического света в спектр. Максимумы коротких длин волн имеют меньший угол дифракции, чем длинных для всех порядков спектра кроме нулевого.
При дифракции на решетке возникают гораздо более узкие и интенсивные максимумы, чем на одной щели, что приводит к большей разрешающей способности решетки. Разрешающая способность спектрального прибора характеризует его возможность разделить излучения с близкими длинами волн. Мерой разрешающей способности принято считать отношение длины волны l, около которой выполняется измерение к интервалу Dl между двумя ближайшими в спектре разрешенными линиями.
|
|
|
Чем больше число штрихов N в решетке, тем выше ее разрешающая способность. Увеличение разрешающей способности означает, что в наблюдаемом спектре можно разделить близко лежащие линии (если, конечно, спектр излучения дискретный).
В работе не предпринимается специальных действий, чтобы обеспечить нормальное падение света на решетку, поэтому необходимо проанализировать вопрос о связи угла дифракции с длиной волны при падении параллельного пучка света под некоторым углом к решетке.
Пусть i - угол между нормалью к поверхности решетки и направлением падения света на решетку, j - угол дифракции, l - длина волны света.
Если углы i и j расположены по разные стороны относительно нормали к решетке (рис.3,а), то условие получения дифракционного максимума принимает вид
d (sinj 1 - sin i) = l k. (7)
Если i и j расположены по одну сторону от нормали, то
d (sinj 2 + sin i) = l k. (8)
При нормальном падении света дифракционная картина будет симметричной относительно главного максимума. В рассматриваемом случае дифракционная картина асимметрична.
| |||
| Рис.3. |
Из рисунка 3с видно, что j1=a1+ i, j2=a2 - i, где a1 и a2 - углы, образованные между нулевым максимумом и соответствующими максимумами слева и справа от нулевого. Складывая уравнения (7) и (8) и подставляя значения j1 и j2, получаем:
d sin(a1+ i) + sin(a2 - i)=2 k l,
откуда после некоторых преобразований следует
 .
.
Учитывая, что угол мал, и, следовательно, cos(i /2) @ 1, эту формулу можно упростить:
 (9)
(9)
Измерив углы a1 и a2, и воспользовавшись известным значением постоянной решетки d, можно определить длины волн спектральных линий.
|
|
|