 |
Образец протокола №1 эксперимента по методу «ДА-НЕТ»
|
|
|
|
Протокол № 1 I серия
| Порядковый номер пробы | Вид пробы | Ответ испытуемого | Исход пробы |
| S | Да | Y/S – правильное обнаружение | |
| n | нет | N/n – правильное отрицание | |
| S | нет | N/S – пропуск стимула | |
| S | да | Y/S – правильное обнаружение | |
| n | да | Y/n – ложная тревога | |
| ... | ... | ... | ... |
| n | нет | N/n – правильное отрицание | |
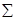 (S) =100 (S) =100
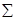 (n) =100 (n) =100
| 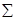 (Y/S) = (Y/S) = 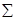 обн = 61 обн = 61
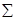 (Y/n) = (Y/n) = 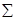 лт = 26 лт = 26
|
В этом протоколе использованы как уже применявшиеся стандартные обозначения, так и новые, а именно:
Вид пробы: S – стимульная (т.е. содержавшая стимул); n – пустая;
Всего из 200 проб 100 было стимульных; а 100 – пустых, что означает равенство априорных вероятностей появления стимула и шума в отдельной пробе: q(S)=q(n)=0,5.
Исход пробы: 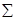 (Y/S) =
(Y/S) = 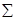 обн = 61 – из 100 предъявлений стимульных проб в 61-й был дан ответ “да” – т.е. было правильное обнаружение стимула;
обн = 61 – из 100 предъявлений стимульных проб в 61-й был дан ответ “да” – т.е. было правильное обнаружение стимула;
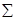 (Y/n) =
(Y/n) = 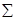 лт = 26 – из 100 предъявлений пустых проб в 26 был дан ответ “да” – т.е. имела место ложная тревога.
лт = 26 – из 100 предъявлений пустых проб в 26 был дан ответ “да” – т.е. имела место ложная тревога.
Соответственно в 39 стимульных пробах был дан ответ типа «N/S» – пропуск стимула, а в 74 пустых пробах – ответ «N/n» – правильное отрицание.
Обработка результатов. Эмпирическими данными, на основе которых рассчитывается показатель чувствительности d¢ и строится PX, являются полученные в эксперименте Pобн и Pлт – вероятности правильного обнаружения и ложной тревоги. Последующая процедура обработки этих данных и получения показателей может быть разбита на 3 этапа:
1) расчет вероятностей правильного обнаружения Pобн и ложной тревоги Pлт;
2) построение графика рабочей характеристики (иногда этап графического представления результатов может быть опущен);
3) расчет показателя чувствительности d¢.
|
|
|
Рассмотрим каждый из этих этапов подробнее.
1) Расчет значенийPобн и Pлт:
Pобн = 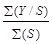 ; (19 a)
; (19 a)
Pлт = 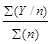 . (19 b)
. (19 b)
Конкретные значения величин в правой части этих формул берутся из протокола эксперимента. Так, для приведенного выше протокола имеем:
Pобн = 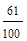 = 0,61; Pлт =
= 0,61; Pлт = 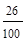 = 0,26.
= 0,26.
Предположим, что в проведенной дополнительно II-ой серии экспериментов при сохранении значения стимула была предпринята попытка изменения величины порога принятия решения λ0 за счет изменения априорных вероятностей стимульных и пустых проб (q1 и q2). В этой дополнительной серии использованы следующие значения априорных вероятностей:
q(S) = 0,75;
q(n) = 0,25,
с соблюдением соотношения q(S) + q(n) = 1. При общем числе проб в экспериментах второй серии, равном 200 – как и в первой серии, имеем следующее количество стимульных и пустых проб:
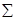 (S) = 150,
(S) = 150,
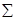 (n) = 50.
(n) = 50.
Протокол эксперимента второй серии по форме будет выглядеть аналогично протоколу первой серии и приведен в табл.7.
Таблица 7
Образец протокола №2 эксперимента по методу «ДА-НЕТ»
Протокол № 2 2 серия
| Порядковый номер пробы | Вид пробы | Ответ испытуемого | Исход пробы |
| S | нет | N/S – пропуск стимула | |
| n | Да | Y/n – ложная тревога | |
| S | да | Y/S – правильное обнаружение | |
| n | нет | N/n – правильное отрицание | |
| S | нет | N/S – пропуск стимула | |
| ... | ... | ... | ... |
| S | да | Y/S – правильное обнаружение | |
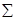 (S) = 150 (S) = 150
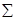 (n) = 50 (n) = 50
| 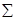 (Y/S) = (Y/S) = 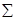 обн = 119 обн = 119
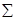 (Y/n) = (Y/n) = 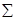 лт = 24 лт = 24
|
Используя алгоритм, уже применявшийся для расчетов Pобн и Pлт в первой серии, во второй серии получаем:
Pобн = 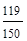 = 0,79;
= 0,79;
Pлт = 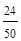 = 0,48.
= 0,48.
Таким образом, изменив значение априорных вероятностей появления стимула в пробе q(S) и его отсутствия q(n), получаем увеличение и Pобн, и одновременно Pлт, что совершенно закономерно.
2) Построение графика PX.
Графически построение PX возможно двумя способами:
а) в линейных координатах (по оси x - Pлт, по оси y - Pобн);
|
|
|
b) в Z-координатах (так называемых «двойных нормальных» координатах: по оси x - Z лт, по оси y - Z обн).
Построение графика РХ в общем виде в обычной системе координат нами уже производилось в 2.2.3 (см. рис.8). При построении РХ этим способом по экспериментальным данным достаточно нанести на поле графика две точки с координатами, полученными в 1 и 2 сериях (рис.13).
Для каждой экспериментальной точки определяются доверительные интервалы (при выбранной доверительной вероятности β) по осям Pобн и Pлт – на рисунке они представлены в виде горизонтальных и вертикальных отрезков, проходящих через экспериментальные точки. На практике построение такой PX применяется редко, так как не дает простого способа графического расчета d¢.
Гораздо чаще встречается построение PX в Z-координатах, которые также называются двойными нормальными координатами, поскольку построены исходя из предположения, что исходные величины подвергаются Z-преобразованию Фишера, опирающемуся на нормальный (гауссовский) закон распределения плотности вероятности. В используемом нами подходе предполагается, что распределения сенсорных эффектов f(s) и f(n) подчиняются именно нормальному закону распределения.
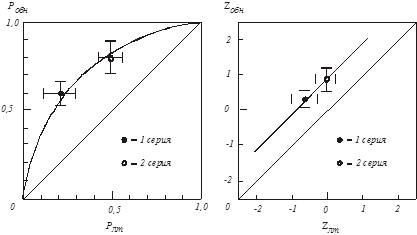
Рис.13. Рабочие характеристики наблюдателя в линейных (слева) и двойных нормальных (справа) координатах (β≤0,95)
Для того, чтобы построить PX в Z-координатах, надо перевести значения Pобн и Pлт в Z-единицы. Сделать это можно, используя специальные таблицы Z-преобразования, где даны рассчитанные значения интеграла нормального распределения, и которые приводятся в любом руководстве по теории вероятности и математической статистике.
Для нашего примера имеем:
I серия: 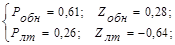
II серия: 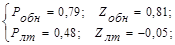
Теперь, используя Z-координаты, строим новый вариант PX (см. рис.13, справа). Функция PX в этих координатах представляет собой прямую, проходящую через экспериментальные точки и параллельную главной диагонали. Понятно, что построить такую линейную функцию гораздо легче, чем сложную кривую, какой является РХ в обычных координатах.
3) Расчет показателя чувствительности d¢.
Полученные выше значения Z обн и Z лт характеризуют, соответственно, расстояние по оси сенсорных эффектов s от MS до критической точки s0 (Z обн ) и от Mn до s0 (Z лт); выраженное в единицах 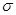 (при условии
(при условии  =
= 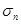 =
= 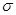 ):
):
|
|
|
Z обн = 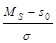 ; (20 a)
; (20 a)
Z лт = 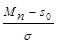 . (20 b)
. (20 b)
Поскольку, по определению (18), имеем:
d¢ = 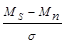 , (21)
, (21)
то, преобразуя это выражение прибавлением и вычитанием в числителе s0, получаем:
d¢ = 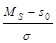 –
– 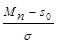 . (22)
. (22)
Последнее выражение можно переписать в более простом виде, используя записанные выше обозначения Z обн и Z лт (20a,b):
d¢ = Z обн – Z лт (23)
Эта формула является основной для расчета количественных значений показателя чувствительности d¢ и используется в подавляющем большинстве работ из-за простоты и легкости ее применения.
Используя формулу (24) для разбиравшихся в этом разделе примеров, получим следующие значения d¢:
I серия: d¢ 1 = 0,28 - (-0,64) = 0,26 + 0,64 = 0,90;
II серия: d¢ 2 = 0,81 - (-0,05) = 0,81 + 0,05 = 0,86.
То есть полученные в первой и второй сериях значения d¢ практически совпали, хотя это и не всегда получается в реальности.
Графически величина d¢ в Z-координатах представляет собой не что иное, как кратчайшее расстояние от любой точки прямой РХ до главной диагонали.
Метод оценки
По ряду своих особенностей метод оценки сходен с методом «Да - Нет»: они полностью идентичны по организации стимульной последовательности и структуре отдельной пробы, но различаются особенностями ответов испытуемых.
Основные правила, на которых базируется метод оценки:
1) использование одного значения стимула;
2) использование пустых проб;
3) использование нескольких категорий ответов. Испытуемый, опираясь на полученные в отдельной пробе впечатления, должен оценить, какова вероятность того, что в данной пробе предъявлялся стимул. При этом испытуемый должен использовать не менее трех вариантов (категорий) ответов. Первая категория ответов испытуемого соответствует вероятности наличия стимула в пробе, близкой к 0, а последняя - вероятности, близкой к 1,0. В реальном эксперименте, как правило, эти категории чаше определяются в инструкции в вербальной форме.
Сравнивая эти правила с теми, которые были у метода «Да – нет», отметим различие только по пункту 3, причем метод «Да – Нет» может рассматриваться как предельный вариант метода оценки, в котором число оценочных категорий сведено к минимуму – к двум.
|
|
|
В табл.8 приведен пример использования числовой и вербальной форм задания пяти оценочных категорий. Числовая форма предполагает задание интервалов значений оценки испытуемым вероятности наличия стимула в каждой пробе - P(S), а вербальная – словесную формулировку степени уверенности-неуверенности испытуемого в том, что в пробе присутствовал стимул. В этой связи некоторые исследователи небезосновательно относят метод оценки к методам шкалирования.
В измерениях дифференциальной чувствительности речь ведется не о наличии-отсутствии стимула в пробе, а о том, есть ли различие между сравниваемыми стимулами.
Из данного примера видно, что фактически в методе оценки испытуемый получает возможность в своих ответах отразить степень своей уверенности в том, что в данной пробе присутствовал стимул. При этом очевидно, что соответствие между интервалами P(s) и их словесным описанием весьма приблизительное и неточное.
Таблица 8
|
|
|


