 |
Определение интервальной оценки
|
|
|
|
Оценивание неизвестных параметров распределения
Предположим, что 
-- независимая выборка из неизвестного распределения 
, зависящего от неизвестного параметра 
. Часто возникает необходимость приблизить значение некоторой функции 
от параметра 
. Функция 
, вообще говоря, может принимать векторные значения:
В математической статистике такая задача называется задачей оценивания. Само искомое приближение называют оценкой. По существу, оценка 
функции есть некоторое выражение, зависящее от выборки:
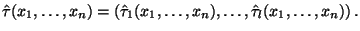
Замечание 6.6
Нередко рассматривают ситуацию 
, 
. В этом случае говорят просто об оценке неизвестных параметров распределения, которую принято обозначать
Сразу возникают три вопроса: какие оценки можно считать хорошими; как сравнивать две оценки по качеству; как строить оценки. Начнем с первого из них.
- Оценка 
называется несмещенной для функции от неизвестного параметра , если
(В случае вектор-функций это равенство следует понимать покоординатно: 
.)
- Последовательность оценок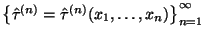 
называется состоятельной, если для любого 
Мы можем кратко записать, что 
состоятельна, если 
при 
.
Таким образом, если известно, что последовательность оценок состоятельна, то при статистической обработке данных имеет смысл увеличивать объем выборки, так как это приведет к более точному результату.
Последовательность оценок 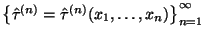называется асимптотически нормальной, если найдутся последовательность вещественных функций 
и последовательность положительных функций 
такие, что
В этом случае говорят, что последовательность 
асимптотически нормальна 
.
Последовательности и не определены однозначно, и далеко не всегда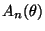 
совпадает с 
, а 
с 
. Понятно, что в силу центральной предельной теоремы асимптотическая нормальность будет характерна в первую очередь для тех оценок, которые связаны с суммами независимых одинаково распределенных слагаемых.
|
|
|
Асимптотическая нормальность является полезным свойством, так как она дает приближенное представление о распределениях оценок при больших конечных значениях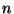 
.
Определение интервальной оценки
Интервальной называют оценку, которая определяется двумя числами – концами интервала.
Допустим, что для изучения некоторой случайной величины X (признака генеральной совокупности) необходимо по статистическим данным произвести оценку неизвестного ее параметра θ (это может быть М(Х), D(Х) или р) с определенной степенью точности и надежности, т. е. надо указать границы, в которых практически достоверно лежит этот неизвестный параметр θ.
Это означает, что надо найти такую выборочную оценку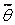 
для искомого параметра θ, при которой с наибольшей вероятностью (надежностью) будет выполняться неравенство:
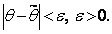
Отсюда видно, что чем меньше e, тем точнее характеризуется неизвестный параметр θ с помощью выборочной оценки 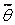. Следовательно, число e характеризует точность оценки параметра θ.
Надежность выполнения неравенства 
оценивается числом g (α = 1 – γ), которое называют доверительной вероятностью:
g = Р ( 
). (1.11)
Итак, число e характеризует точность оценки параметраθ; число g – характеризует надежность оценки параметра θ.
В практических задачах либо заранее задается надежность g (риск α) и надо найти точность оценки, либо, наоборот, задается точность e, а требуется определить надежность оценки.
Как правило, доверительную вероятность g задают числом, близким к единице: 0,95; 0,97; 0,99; 0,999.
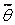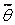Формула (1.11) означает, что с вероятностью g неизвестное значение параметра θ находится в интервале Ig = ( – e, + e).
|
|
|
Очевидно, чем больше требуется точность e (т. е., чем меньше длина интервала), тем меньше вероятность накрыть интервалом I g искомый параметр θ, и, наоборот, с уменьшением точности e (увеличением длины интервала) увеличивается надежность g накрыть интервалом I g параметр θ (рис. 1.5).
Рис. 1.5. Доверительный интервал
Существует два подхода к построению доверительных интервалов. Первый подход, если его удается реализовать, позволяет строить доверительные интервалы при каждом конечном объеме выборки п. Он основан на подборе такой функции 
, называемой в дальнейшем статистикой, чтобы
1) ее закон распределения был известен и не зависел от θ;
2) функция была непрерывной и строго монотонной по θ.
Задавшись доверительной вероятностью γ, связанной с риском α формулой γ = 1 – α, находят двусторонние критические границы 
и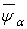 
, отвечающие вероятности α. Тогда с вероятностью γ выполняется неравенство
(1.12)
Решив это неравенство относительно θ, находят границы доверительного интервала для θ. Если плотностьраспределения статистики симметрична относительно оси Оу, то доверительный интервал симметричен относительно .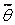
Второй подход, получивший название асимптотического подхода, более универсален; однако он использует асимптотические свойства точечных оценок и поэтому пригоден лишь при достаточно больших объемах выборки.
|
|
|
