 |
Переходные процессы решения дифференциальных уравнений операторным методом
|
|
|
|
Сущность операторного метода. Некоторая функция вещественной переменной t, удовлетворяющая условию Дирихле (на конечном промежутке времени функция должна иметь конечное число разрывов первого рода и должна быть периодической), в момент времени 
, 
сопоставляется с функцией комплексной переменой 
(
– комплексная переменная).
В данном случае функция вещественной переменной 
называется оригиналом, а функция комплексной переменной – изображением.
Переход от оригинала к изображению, и наоборот, осуществляется с помощью прямого 
и обратного 
преобразований Лапласа.
Математически можно записать, что функция является изображением функции , следующим образом:
или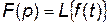 
,
а функция f (t) оригиналом F (p):
или 
.
Оригинал функции можно найти и с помощью теоремы разложения. Если изображение функции представлено в виде дроби 
, причем многочлены (относительно р) N (p) и M (p) удовлетворяют следующим условиям: степень N (p) ниже степени M (p), ак и bk – вещественные числа, а корни р1, р2, …, рn уравнения M (p) = 0 различны, тооригинал находим по формуле 
, где М`(рк) – значение производной при р = р к, N (р к) – значение числителя при р = р к.
В том случае, если один из корней равен нулю, то
,
М (0) и N (0) – значение знаменателя и числителя соответственно при р к = 0.
Если имеются корни кратностью mk, то оригинал вычисляется по формуле 
.
Кроме вышеперечисленных способов нахождения оригинала и изображения функции, их можно определить с помощью созданных программных продуктов, таких, например, как Mathcad или с помощью специальных таблиц, которые приводятся в справочниках по высшей математике или в учебных пособиях по ТОЭ [3, 9]. Таблица оригиналов и изображений по Лапласу приводится и в данном издании (прил. 2).
|
|
|
При нахождении изображения (оригинала) сложной функции следует помнить, что переход от оригинала к изображению, и наоборот, осуществляется с помощью интегрального преобразования и поэтому:
,
.
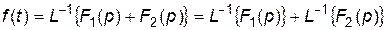Использование преобразований Лапласа при расчете переходных процессов в электрических цепях позволяет перейти от системы интегрально-дифференциальных уравнений, описывающих электромагнитные процессы к системе алгебраических уравнений, что существенно упрощает процедуру нахождения искомых токов и напряжений в цепи.
Передаточная функция, амплитудно фазовые частотные характеристики (АФХЧ)-определения,примеры
Амплитудно-фазовая частотная характеристика (АФЧХ) — удобное представление частотного отклика линейной стационарной динамической системы в виде графика в комплексных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и амплитуда системы на заданной частоте представляется углом и длиной радиус-вектора каждой точки характеристики. По сути такой график объединяет на одной плоскости амплитудно-частотную и фазо-частотную характеристики.
Термин употребляется также в жопе к передаточной функции системы, записанной в виде преобразования Фурье выходного сигнала, поделённого на преобразование Фурье входного сигнала.
Фазо-частотная характеристика (ФЧХ) - графическое отображение зависимости сдвига по фазе между входным и выходным сигналами в зависимости от частоты,
Для определения числитель 
и знаменатель W(j) разлагаются на множители не выше второго порядка
,
тогда, где знак "+" относится к i=1,2,...,l (числителю передаточной фунции), знак "-" -к i=l+1,...,L (знаменателя передаточной функции).
РИС. ПРИМЕР АФХЧ
|
|
|
