 |
Муниципальное автономное общеобразовательное учреждение лицей №44 Г. Липецка
|
|
|
|
Тема: «Многогранники. Применение и роль многогранников в искусстве, а именно в архитектуре и живописи».
Автор: Кузнецова Юлия Андреевна,
ученица 10 Д класса,
Научный руководитель: Царькова Татьяна Николаевна,
учитель математики.
Липецк, 2017
Содержание:
I. Введение: введение в план работы.
II. Основная часть:
1) Определение и виды многогранника.
2) Познакомиться с историей возникновения многогранников.
3) Решение (подборка) задач по теме «многогранники» из ЕГЭ
4) Многогранники в архитектуре.
5) Многогранники в живописи.
6) Смоделировать модель многогранника, на примере предмета из жизни.
III. Заключение: вывод о проделанной работе.
I. Актуальность темы:
Тема «Многогранники» одна из основных в традиционном курсе школьной геометрии. Они составляют, можно сказать, центральный предмет стереометрии.Центральная роль многогранников определяется, прежде всего, тем, что многие результаты, относящиеся к другим телам, получаются исходя из соответствующих результатов для многогранников.Кроме того, многогранники сами по себе представляют чрезвычайно содержательный предмет исследования, выделяясь среди всех тел многими интересными свойствами, специально к ним относящимися теоремами и задачами. Так же они дают особенно богатый материал для развития пространственных представлений, для развития того соединения живого пространственного воображения со строгой логикой, которое составляет сущность геометрии. Более того многогранники встречаются не только в курсе геометрии, но и в искусстве, а именно в архитектуре и живописи.
Объект: многогранники
Предмет: применение многогранников в архитектуре и живописи
|
|
|
Цель:
· Узнать, как используются многогранники в искусстве, а именно в архитектуре и живописи, чтобы понять значимость многогранников в мире.
Задачи:
· Изучить историю возникновения многогранников
· Изучить виды многогранников
· Познакомиться с задачами по многогранникам из ЕГЭ
· Выяснить, как геометрическая фигура «многогранник» используется в архитектурных сооружениях и в написании картин.
· Выбрать предмет из архитектуры или живописи, где присутствует многогранник и на его примере сделать схему этого многогранника.
Гипотеза:
Я думаю, что многогранники важны и интересны не только в науке, но и в искусстве тоже, а именно в архитектуре и живописи.
Значимость проекта:
После изучения проекта учащиеся:
· получат последовательную систему теоретических знаний по теме «Многогранники».
· Узнать (выяснить), как применяются многогранников в искусстве.
· Поймут значимость многогранников в нашем окружении.
Вывод:
Я подробно изучу тему «многогранники» и познакомлюсь с задачами из ЕГЭ по этой теме. Узнаю применение многогранников в живописи и архитектуре. Научусь делать схему многогранника по выбранному мною предмету.
II.
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые
глубины различных наук.
Кэрролл Л
1. Определение:
Многогранник - часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого смежным), причем вокруг каждой вершины существует ровно один цикл многоугольников.
Виды многогранника:
Пирамида -это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной.
|
|
|
· Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника.
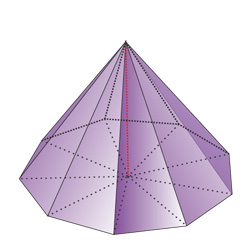
· Пирамида называется усеченной, если вершина её отсекается плоскостью
Призма - многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы.
· Призма называется прямой, если её ребра перпендикулярны плоскости основания.
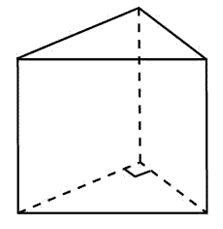
· Если основанием призмы является прямоугольник, призму называют параллелепипедом
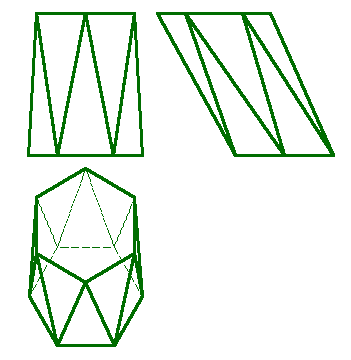
· Призматоид - многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований
Правильный многогранник -многогранник, все грани которого представляют собой правильные и равные многоугольники. Углы при вершинах такого многогранника равны между собой.Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.
· Тетраэдр -правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (это - правильная треугольная пирамида).
· Гексаэдр - правильный шестигранник. Это куб, состоящий из шести равных квадратов.
· Октаэдр - правильный восьмигранник. Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.
· Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины.
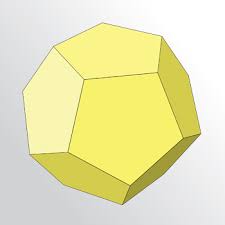
· Икосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины
· Звездчатый октаэдри малый звездчатый додекаэдр-
- восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые "куски", внешние по отношению к октаэдру.
2. История возникновения многогранников
Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.
|
|
|
История правильных многогранников уходит в глубокую древность. Начиная с 7 века, до нашей эры в Древней Греции создаются философские школы. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства. Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.
Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики - это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.
Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел:
- Вселенная - додекаэдр
- Земля - куб
- Огонь - тетраэдр
- Вода - икосаэдр
- Воздух - октаэдр
Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ - идеалист Платон. С тех пор правильные многогранники стали называться платоновыми телами.
Платон также считал, что мир строится из четырёх «стихий», а атомы этих «стихий» имеют форму четырёх правильных многогранников.
В наше время эту систему можно сравнить с четырьмя состояниями вещества - твёрдым, жидким, газообразным и пламенным. Пятый многогранник - додекаэдр символизировал весь мир и почитался главнейшим. Это была одна из первых попыток ввести в науку идею систематизации.
|
|
|
Для трехмерного пространства существует всего пять правильных многогранников:
| Многогранник | Грани | Вершины | Ребра |
| Тетраэдр | 4 треугольника | 4 | 6 |
| Октаэдр | 8 треугольников | 6 | 12 |
| Гексаэдр (куб) | 6 квадратов | 8 | 12 |
| Икосаэдр | 20 треугольников | 12 | 30 |
| Додекаэдр | 12 пятиугольников | 20 | 30 |
Открытие тринадцати полуправильных выпуклых многогранников приписывается Архимеду, которые позже в честь великого ученого были названы телами Архимеда. Архимедовы тела, частично получаются из Платоновых тел в результате их усечения.
Открытие многогранников сильно помогло людям в разных отраслях деятельности, особенно в архитектурной и живописной сфере.
3. Решение (подборка) задач по теме «многогранники» из ЕГЭ
Тема многогранников, так же присутствует в задачах единого государственного экзамена (ЕГЭ) в заданиях С2. Например:
1) Найти площадь поверхности многогранника. 
Решение: из площади поверхности вычитаем площади двух квадратов со стороной 1-на верхней и нижней гранях.
Ответ: 92
2) Объем параллелепипеда равен 
. Найдите объем треугольной пирамиды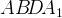 
.
Решение: Мы помним, что объем параллелепипеда равен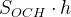 
. А объем пирамиды равен 
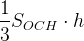. Иными словами, если у параллелепипеда и пирамиды одинаковые основания и одинаковые высоты, то объем пирамиды будет в три раза меньше, чем объем параллелепипеда. А у нашей пирамиды еще и площадь основания в два раза меньше. Значит, ее объем в шесть раз меньше объема параллелепипеда.
Ответ: 1,5.
3) Найдите объем 
конуса, образующая которого равна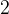 
и наклонена к плоскости основания под углом 
градусов. В ответе укажите .
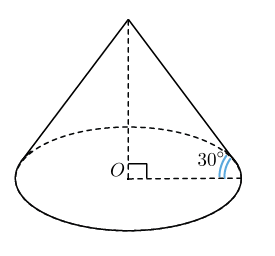
Решение: Вспомним, что угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость, то есть угол 
.
Из прямоугольного треугольника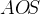 
находим, что 
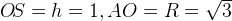. Объем конуса найдем по известной формуле и поделим на 
.
Ответ: 1.
4)Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 
раза?
Решение: Если все ребра многогранника увеличить в три раза, площадь поверхности увеличится в раз, поскольку 
.
Ответ: .
5) В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1 = 1, CD = 2, AD = 2. Найдите длину диагонали CA1.
Решение: d 2 = a 2 + b 2 + c 2
d - любая диагональ прямоугольного параллелепипеда, a,b,c - три его характерных размера, каким бы образом их не задали. Поэтому
d 2 = 12 + 22 + 22 = 1 + 4 + 4 = 9. d = 3. Следовательно, диагональ CA 1 = 3.
Ответ: 3
Здесь представлены, примеры самых распространенных задач, которые встречаются на ЕГЭ. Больше всего встречаются задачи на нахождения объема, площади и диагоналей различных многогранников, а так же задачи на теорию и свойства.
|
|
|
4. Многогранники в архитектуре:
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Кэрролл Л.
В XIII-XVII вв. многогранники были основой архитектурных строений, больше всего применялись кубы, но по мере развития нашли применения и другие виды многогранников. В наши дни невозможно обойтись без многогранников, так как они окружают нас практически везде, например, различные здания, торговые центры, архитектурные строения, предметы - во всем этом обязательно будут присутствовать многогранники, стоит только присмотреться.
5. Многогранники в живописи:
Примерно с ХIIIв. Художники начали экспериментировать с изображением пространства. Они «создавали» живописное пространство, изменяя размеры фигур, располагая по определенным правилам элементы архитектуры, детали ландшафта. В результате чего появилось новое направление в искусстве и живописи- импрессионизм.
|
|
|
