Интерполяционные квадратурные формулы. Квадратурные формулы наивысшей алгебраической степени точности.

Алгебраическое интерполирование. Исследование существования и единственности интерполяционного полинома. Интерполяционный полином Лагранжа. Оценка остаточного члена.

Пусть имеется значения функци f(x_i) в нектр точках x₀,x₁,x₂,¼,x_n, x_i Î [a,b] "I, x₀=a<x₁<…<x_n=b. Требуется построить функцию g(x), такую что, f(x_i)=g(x_i), i=0,1,2,¼,n. (1)
Задача построения такой функции g(x) называется задачей интерполяции. Точки x₁,x₂,¼,x_n называются узлами интерполяции.
Как правило, функция g(x) ищется из некоторого наперед заданного класса функций, назовем его V. Если элементами V являются полиномы, то говорят об алгебраической интерполяции, при этом функцию g(x) называют интерполяционным полиномом.
Говорят, что задача интерполяции поставлена корректно, если при любых значениях f(x_i), i=1,2,¼,n, существует единственная функция g(x) из V, удовлетворяющая условиям (1).
Исследуем корректность задачи алгебраической интерполяции.
Пусть g(x) = a₀+a₁ x+¼+a_m x^m. Коэффициенты a_i определяются условиями (1), то есть являются решением следующей системы линенйых уравнений
å_i=0^m a_i x_jⁱ = f(x_j), j=0,1,2,¼,n. (2)
При m=n число неизвестных данной системы будет равно числу уравнений в ней, а определитель системы будет иметь вид Это - определитель Вандермонда, его значение D = Õ_{i > j} (x_i-x_j). Поэтому D отличен от нуля(все узлы интерполяции различны). Итак, задача алгебраической интерполяции корректна, если при заданных n+1 различных узлах интерполяции, функцию f(x) приближать полиномом степени n.

Рассмотрим вопрос построения интерполяционного полинома. Его коэффициенты можно найти, решая систему (2). Однако, очевидно что многочлен степени n удовл.условиям (2) имеет вид:

P_n(x) = Сумма(f(x_i) * Ф_i(x)), i=0,n; где Ф_i(x) = Произв.((x-x_i)/(x_i-x_j)); j=0,n; i<>j, i=0,n

(если нужно)

Интерполяционный полином, записанный в такой форме, называют интерполяционным полиномом Лагранжа и обозначают через L_n(x):
Оценку погрешности интерполяционного полинома будем проводить в предположении, что функция f(x) имеет непрерывные производные вплоть до порядка n.

Теорема

Пусть f(x) непрерывна (n+1) раз на [a,b]; сущесвтует x на [a,b], что

f(x) – Ln(x) =(f⁽ⁿ⁺¹⁾(x) / (n+1)!) *w_n+1(x)

 

(кому нужно)
Рассмотрим функцию j(x)=f(x)-L_n(x)-K w_n+1(x) (4) где K - некоторая постоянная, w_n+1(x)= (x-x₀) (x-x₁)¼(x-x_n). Пусть z Î [a,b] - точка, в которой мы хотим получить оценку остаточного члена. Естественно предположить, что
z¹x_i, i=1,¼,n. Выберем K из условия j(z)=0. Это значение постоянной K можно выразить через производную порядка n функции f. По построению j(x_i)=0, i=1,¼,n. Поэтому на отрезке [a,b] функция j обращается в нуль n+1 раз. По теореме Ролля ее первая производная должна обращаться в нуль на [a,b] хотя бы в n точках, а соответственно j⁽ⁿ⁾ - хотя бы в одной точке. Пусть это будет точка x. Имеем j⁽ⁿ⁾(x) = f⁽ⁿ⁾(x) -0-K n!
Отсюда следует, что K = f⁽ⁿ⁾(x)/ n!. Из (4), учитывая, что j(z)=0, будем иметь

Требуемая оценка получена.

 

Max| w_n+1(x)| на [-1;1] - будет наименьшей, если в качестве узлов интерполяции взять корни многочлена Чебышева:

Tn(x) = cos(n*arcos(x)), |x|<=1

 

Интерполяционные квадратурные формулы. Квадратурные формулы наивысшей алгебраической степени точности.

Формулы, позволяющие получать приближенное значение определенного интеграла, называются квадратурными.

Формула:

называется квадратурной формулой, числа q_i – называются весами квадратурной формулы, R –погрешность квадратурной формулы. Квадратурная формула считается заданной, если указано как выбирать x_i. Соотвеств им веса квадратр.формулы q_i и дана оценка погрешности R для определенных классов функции. Квадратурная формула нзв точной для нектр класса функций, если в этой формуле R=0 сразу для всего класса функций.

Опишем один из способов построения квадратурных формул на примере вычисления интеграла вида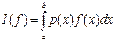
здесь p(x) - фиксированная функция, положительная на отрезке [a,b] за исключением быть может конечного числа точек, в которых она обращается в нуль. Функцию p(x) принято называть весом; функция f произвольна. Заменим на отрезке [a,b] функцию f интерполяционным полиномом Лагранжа
построенным по узлам x_i, i=1,¼,n, принадлежащим отрезку [a,b]. В результате будем иметь

Построенная таким образом квадратурная формула называется интерполяционной, точки x_i называют узлами квадратурной формулы, числа c_i - весами квадр.формулы.
Говорят также, что квадратурная формула имеет алгебраическую степень точности m, если она точна на любом полиноме, степень которого не больше m.

Отметим основные свойства интерполяционных квадратурных формул.
Теорема 1. Интерполяционная квадратурная формула (1) точна на любом полиноме степени n.
Док-во. Из теории интерполирования известно, что, если f - полином степени n, то L_n (x) = å_j=0ⁿ f(x_j) F_i(x) º f(x). Поэтому (см. (1)) I(f)=S_n(f). Теорема доказана.

 

При построении интерполяционной квадратурной формулы (1) выбор узлов x_i был произволен, предполагалось лишь, что они различны. Но это квадратурная формула при n>=1 является точной на классе многочленов 1-й степени (P₁(x)).

Если же точки x_i на отрезке [a,b] выбирать специальным образом, то можно построить интерполяционные квадратурные формулы более высокой алгебраической степени точности.

Опр. Интерполяционные квадратурные формулы, построенные по n+1 узлу, алгебраическая степень точности которых равна 2n+1, называют квадратурными формулами наивысшей алгебраической степени точности.

Теорема 3. Интерполяционная квадратурная формула является квадратурной формулой наивысшей алгебраической степени точности тогда и только тогда, когда ее узлами являются корни полинома степени n, ортогонального на отрезке [a,b] с весом p(x).
Док-во кому нужно. Напомним, что полином Q_n степени n называется ортогональным полиномом на отрезке [a,b] с весом p(x), если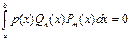
для любого полинома P_m, степень которого m £ n-1. Известно, что все корни ортогонального на отрезке [a,b] полинома различны и принадлежат отрезку [a,b].
Пусть квадратурная формула S_n интерполяционная, а ее узлы являются корнями ортогонального многочлена Q_n. Докажем, что ее алгебраическая степень точности равна 2n-1. Для этого произвольный полином P_2n-1 степени 2n-1 представим в виде P_2n-1(x) = Q_n(x) q_n-1(x) + r_n-1(x),
где q_n-1 и r_n-1 - полиномы, степень которых не превосходит n-1. Из ортогональности многочлена Q_n следует, что
С другой стороны, поскольку x_i - корни многочлена Q_n, то

Теор. НЕ сущ.таких узлов xi и весов qi чтобы формула (1) была точна для любого многочлена P2n+2(x).

Убедимся в том, что по n различным узлам нельзя построить квадратурную формулу более высокой алгебраической степени точности. Предположим, что существует квадратурная формула, алгебраическая степень точности которой 2n. Тогда она точна на полиноме (w_n)², то есть справедливо равенство
Однако правая часть этого равенства, как интеграл от неотрицательной функции, не равной тождественно нулю, строго положительна, а левая равна нулю, поскольку x_i - корни полинома w_n. Полученное противоречие свидетельствует о неверности предпосылки, то есть квадратурной формулы, алгебраическая степень точности которой равна 2n, не существует.

(*) – квадратурная формула Гаусса.

Практический смысл квадратурных формул проявляется при интегрировании таких классов функций, ктр могут быть хорошо аппроксимированы многочленами

 

74. Метод Гаусса решения систем линейных уравнений. Применение метода Гаусса к вычислению определителя и обратной матрицы.

Одним из наиболее распространенных и универсальных методов решения систем линейных уравнений является метод Гаусса. Он имеет много различных модификаций. Простейшая его схема состоит в следующем.

Рассмотрим систему линейных уравнений:
Предположим, что a₁₁ ¹ 0. Разделим на a₁₁ первое уравнение системы и с его помощью исключим переменную x₁ из остальных уравнений системы (1). В результате получим

Далее, предполагая a22(1)¹0, разделим на этот коэффициент второе уравнение системы (2) и с его помощью исключим переменную x2 из всех уравнений системы (2), кроме первого. Это приведет нас к эквивалентной (1) системе уравнений вида

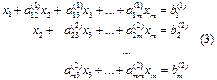
Проводя аналогичные преобразования, через m шагов придем к системе уравнений с треугольной матрицей

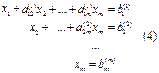
Решение системы (4) не вызывает затруднений, так как компоненты xi могут быть вычислены, начиная с номера m, по следующим формулам

 

Описанный способ получения системы (4) из системы (1) называют прямым ходом метода Гаусса, а решение системы (4) по формулам (5) - обратным ходом.
Оценим количество арифметических операций, необходимых для реализации описанного алгоритма. Анализируя первый этап алгоритма, то есть переход от системы (1) к системе (2), нетрудно подсчитать, что его реализация требует m операций деления, m(m-1) операций умножения и (m-1)(m-2) операций вычитания. При переходе от системы (2) к системе (3) первая строка и первый столбец матрицы системы (2) не преобразуются, поэтому потребуется m-1 операция деления, (m-1)(m-2) операций умножения и (m-2)(m-3) операций вычитания. Ясно, что тогда общее количество операций, необходимых для реализации прямого хода будет равно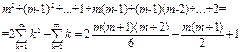
Вычисления по формулам (5) потребуют 1+2+¼+(m-1) операций умножения и столько же операций вычитания. Таким образом, при больших m общее число операций, необходимых для реализации метода Гаусса, приблизительно равно 2m³/3.
Вычисление определителя матрицы с помощью метода Гаусса.
Обозначим A - матрицу системы (1), A⁽¹⁾ - матрицу системы (2), A⁽²⁾ - матрицу системы (3) и, наконец, A^(m) - матрицу системы (4). Заметим, что при переходе от системы (1) к (2) единственной операцией, изменяющей значение определителя, была операция деления на a₁₁, при этом |A|=a₁₁ |A⁽¹⁾|. Аналогичная ситуация имела место и на всех последующих шагах. Поэтому будут справедливы следующие равенства |A| = a₁₁ |A⁽¹⁾| = a₁₁ a₂₂⁽¹⁾ |A⁽¹⁾| = ¼ = a₁₁ a₂₂⁽¹⁾ ¼ a_{m-1 m-1}^(m-1) |A^(m)|.

Поскольку определитель матрицы A^(m) равен 1, то |A| = a₁₁ a₂₂⁽¹⁾ ¼ a_{m-1 m-1}^(m-1), и для отыскания определителя матрицы достаточно реализовать ту часть прямого хода метода Гаусса, в которой преобразуются элементы матриц A⁽ⁱ⁾.
Обращение матриц с помощью метода Гаусса.
По определению обратной матрицы A A^-1 = E. (6)
Пусть y^k - вектор, совпадающий с k-тым столбцом матрицы A, а e^k - единичный вектор, совпадающий с k-тым столбцом матрицы E. Тогда матричное равенство (6) можно записать в виде следующих систем линейных уравнений Ay^k=e^k, k=1,2,¼,m, (7) решение которых, очевидно, эквивалентно отысканию матрицы A^-1. Каждую из систем (7) можно решить с помощью метода Гаусса. Однако при организации вычислений следует помнить, что все системы в (7) имеют одну и ту же матрицу A. Поэтому целесообразно прямой ход в методе Гаусса проводить сразу для всех систем, преобразуя элементы матрицы и правые части всех уравнений (7) одновременно. Обратный ход метода Гаусса для каждой системы проводится отдельно. Нетрудно проверить, что число арифметических операций, необходимых для реализации этого алгоритма, остается пропорциональным m³.

Поделиться:

Воспользуйтесь поиском по сайту: