Аксиомы теории вероятности

Содержание

Введение

1. Вероятность как событие

2. Вероятность и информация

3. Аксиомы теории вероятности

Заключение

Список литературы

Введение

 

Каждый эксперимент заканчивается каким-то определенным результатом, который не всегда возможно заранее предугадать. Для того, чтобы формально описать некоторый эксперимент, нужно указать все возможные варианты результатов, которыми этот эксперимент может закончиться. В теории вероятностей такие результаты называются исходами. Множество W всех возможных исходов эксперимента называется пространством элементарных исходов. Предполагается, что эксперимент может закончиться одним и только одним элементарным исходом. В наиболее простом случае все эти исходы можно перечислить:

W = íw₁, w₂,... w_ný, или W= íw₁, w₂,...ý.

Такое пространство элементарных исходов называется дискретным.

Простейшим пространством элементарных исходов является такое пространство, в котором все указанные исходы рассматриваемого эксперимента:

1) равновозможны;

2) взаимно несовместны (т.е. в результате эксперимента может произойти один и только один из указанных исходов),

3) все исходы образуют полную группу событий (т.е. никакие другие исходы, кроме перечисленных, не могут произойти).

Такое пространство конечно и называется пространством равновозможных исходов (или симметричным пространством).

ПРИМЕР 1. При бросании симметричной монеты возможны два исхода – выпадение решки или герба. Они удовлетворяют всем трем указанным выше условиям и потому в этом случае пространство элементарных исходов представляется так (здесь буквами Р и Г обозначены решка и герб соответственно):

ПРИМЕР 2. При одновременном бросании двух монет исходы представляют собой упорядоченные пары, состоящих из символов Р и Г. Первый элемент этой пары – результат, выпавший на первой монете, второй элемент – результат на второй монете. Очевидно, что таких пар – четыре:

ПРИМЕР 3. В случае бросания игральной кости может выпасть любое из чисел 1, 2, 3, 4, 5, 6. Поэтому пространство элементарных исходов

ПРИМЕР 4. При одновременном бросании двух игральных костей элементарные исходы представляют собой пары (x, y), где x – число очков, выпавшее на первой кости, а y – число очков на второй кости. Всего таких пар – 36:

 

Вероятность как событие

 

В дискретном пространстве вероятность каждого элементарного исхода считается заданной и обозначается Р(w_i), или просто р_i , причем всегда

 

1) р_i ³ 0

2)  (или ),

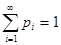3)

т.е. сумма (конечная или бесконечная) вероятностей всех элементарных исходов равна единице. Элементарные исходы мы называем элементарным событием.

Событием   называется любое подмножество, состоящее из элементарных исходов пространства элементарных событий W. Говорят, что «событие А произошло», если эксперимент закончился одним из элементарных исходов w_iÎА.

Вероятностью события А называется сумма вероятностей всех элементарных исходов, входящих в А, то есть Р(А)= . Из этого определения вероятности события следует, что всегда 0 £ Р(А) £ 1.

В случае равновозможных исходов вероятность элементарного события А определяется формулой

,

где  – число элементов во множестве W, которое обычно называется «общее число исходов», а  – число элементов во множестве A, называемое «числом благоприятствующих исходов».

Событие `А, состоящее из всех элементарных исходов, не входящих в А, называется противоположным событием к событию А. Оно происходит тогда и только тогда, когда событие A не произошло. Очевидно что Р(А) + Р(`А) = 1. Это равенство используется для вычисления вероятности события А в случае, когда вероятность противоположного события известна или легко может быть найдена, тогда Р(А) = 1 - Р(`А).

Таким образом, для вычисления вероятности в каждой задаче важно определить, в чем состоит эксперимент, правильно построить соответствующее пространство элементарных событий W и выделить в нем требуемое событие A. Затем, используя методы комбинаторики, подсчитать число элементов в W и A.

Задача 1. В ящике 5 апельсинов и 4 яблока. Наудачу выбираются 3 фрукта. Какова вероятность, что все три фрукта – апельсины?

Решение. Элементарными исходами здесь являются выборки, включающие 3 фрукта.

Решение. Так как порядок здесь безразличен, будем считать выборки неупорядоченными (и, разумеется, бесповторными). Общее число элементарных исходов  равно числу способов выбрать 3 элемента из 9, т.е. числу сочетаний n= . Число благоприятных исходов m= 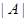будет равно числу способов выбора трех апельсинов из имеющихся 5, т.е. числу сочетаний трех элементов из 5, т.е. 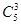. Тогда вероятность

.

Задача 2. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым из студентов любого числа из заданных равновозможен, найти вероятность того, что у кого-то из них задуманы числа совпадут.

Решение. Подсчитаем сначала общее количество исходов. Элементарными исходами будем считать упорядоченные совокупности задуманных чисел: N₁, N₂, N₃, где N₁ - число, задуманное первым студентом, N₂ - вторым и N₃ - третьим Первый из них выбирает одно из 10 чисел — 10 возможностей, второй делает то же самое — 10 возможностей, наконец, выбор третьего также 10 возможностей. Согласно основной теоремы комбинаторики общее число способов будет равно:

n= N₁´N₂´N₃=10³ = 1000 элементарных исходов.

Подсчет количества благоприятных исходов более сложен. Заметим, что совпадение задуманных чисел может произойти у любой пары студентов (или даже одновременно у всех троих). Чтобы не разбирать отдельно все эти случаи, удобно перейти к противоположному событию, т.е. подсчитать количество тех случаев, когда все три студента задумывают разные числа. Первый из них по-прежнему имеет 10 способов выбора числа. Второй студент теперь имеет лишь 9 возможностей (поскольку ему приходится заботиться о том, чтобы его число не совпало с задуманным числом первого студента N₂ ¹ N₁. Третий студент еще более ограничен в выборе — у него всего 8 возможностей (из 10 возможных для N₃ исключаются два числа: N₃ ¹ N₁, N₃ ¹ N₂). Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, равно в силу той же основной теоремы m=10 × 9 × 8 = 720. Остальные случаи 1000 - 720 = 280 характеризуются наличием хотя бы одного совпадения. Следовательно, искомая вероятность совпадения равна Р=280/1000= 0,28.

Задача 3. Найти вероятность того, что в 8-значном числе ровно 4 цифры совпадают, а остальные различны.

Решение. Событие А={8-значное число содержит 4 одинаковые цифры}. Из условия задачи следует, что в числе 5 различных цифр, одна из них повторяется - число способов её выбора - любая из 10 цифр, и эта цифра занимает любые 4 места в числе – число способов . Оставшиеся 4 места занимают различные цифры из неиспользованных 9, и так как число зависит от порядка расположения цифр, то число способов выбора четырех цифр равно . Тогда число благоприятствующих исходов . Всего же способов составления 8-значных чисел равно |W|=10⁸. Искомая вероятность равна .

Задача 4. Шесть клиентов случайным образом обращаются в 5 фирм. Найти вероятность того, что хотя бы в одну фирму никто не обратится.

Решение. Рассмотрим обратное событие , состоящее в том, что в каждую из 5 фирм обратился клиент, тогда в какую-то из них обратились два человека, а в остальные 4 фирмы – по одному клиенту. Таких возможностей . А всего способов распределить 6 клиентов по 5 фирмам . Отсюда 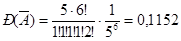, следовательно .

Задача 5. Среди 25 экзаменационных билетов имеется 5 «счастливых» и 20 «несчастливых». Студенты подходят за билетами один за другим по очереди. У кого больше вероятность вытащить «счастливый» билет: у того, кто подошел первым, или у того, кто подошел вторым?

Решение. Пусть «счастливые» билеты имеют номера 1,2,3,4,5. Обозначим через i₁ номер билета, взятого первым студентом, через i₂ - номер билета, взятого вторым студентом, тогда элементарным исходом будет пара 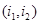, а пространство элементарных исходов

 

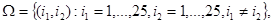
здесь все элементарные исходы равновероятны. Событие А={первый студент взял «счастливый» билет} имеет вид

а событие В={второй студент взял «счастливый» билет} имеет вид:

Каждое из событий А и В содержит 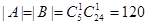 элементов, а все пространство W содержит элементов. Следовательно, Р(А)=Р(В)=1/5.

 

Вероятность и информация

 

Рассмотрим n-мерное вещественное пространство . Пусть в какую-то ограниченную область 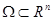 наудачу бросили точку. Слово «наудачу» означает, что в таком эксперименте все точки области  «равновозможны». В этом случае вероятность попадания этой точки в какую-то подобласть  определяется формулой

 

 

гд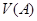е  и  – n-мерные объемы областей  и  соответственно. Здесь элементарными исходами называются точки множества  (которое играет роль пространства элементарных исходов), а благоприятствующими исходами – точки множества .

Задача 6. Точку наудачу бросили на отрезок . Какова вероятность попадания этой точки на интервал ?

Решение. Здесь пространство элементарных исходов весь отрезок 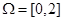, а множество благоприятствующих исходов , при этом длины этих интервалов равны 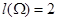  и 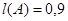. Поэтому вероятность попадания брошенной точки в указанный интервал равна .

Задача 7. На отрезок 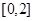 бросили наудачу и поочередно две точки. Какова вероятность, что первая точка лежит правее второй точки?

Решение. Обозначим получившиеся координаты точек через x и y. Элементарным исходом в таком бросании двух точек будет пара , а пространством элементарных исходов – квадрат 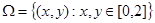. Событие A={первая точка лежит правее второй точки} равносильно условию x>y, следовательно,

, т.е. представляет собой треугольник (см. рисунок). Площади квадрата и треугольника равны соответственно  и , а потому вероятность .

 

Аксиомы теории вероятности

 

Суммой двух событий А и В называется событие АÈВ (А+В), заключающееся в том, что произойдет хотя бы одно из событий А или В (либо событие А, либо событие В либо А и В одновременно).

Произведением ( или пересечением)двух событий А и В называется событие АÇВ (АВ), состоящее в одновременном появлении и события А и события В.

Вероятность суммы двух событий вычисляется по формуле (теорема сложения)

 

.

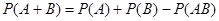События А₁,А₂,...,А_к образуют полную группу событий, если в результате испытания непременно произойдет одно из них, т.е. .

События А и В называются несовместными (непересекающимися), если они не могут произойти одновременно АÇВ=Æ. Если события несовместны, то

Р(АВ) = 0 и Р(А + В) = Р(А) + Р(В).

Задача 1. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?

Решение. Событие A={вынуты пуговицы одного цвета} можно представить в виде суммы , где события  и 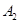 означают выборку пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна , а вероятность вытащить две синие пуговицы . Так как события и 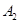не могут произойти одновременно, то в силу теоремы сложения

 

 

Помимо обычной (безусловной) вероятности можно рассматривать так называемую условную вероятность, вычисляемую при условии, что событие B произошло. Такую вероятность (вероятность А при условии В) обозначают Р(А|В) и вычисляют с помощью одной из двух формул:

 

 

Из этой формулы вытекает формула для вероятности произведения двух событий (теорема умножения)

.

 

Формула умножения для трех событий:

 

.

 

Задача 2. В семье – двое детей. Какова вероятность, что старший ребенок – мальчик, если известно, что в семье есть дети обоего пола?

Решение. Пусть А={старший ребенок – мальчик}, B={в семье есть дети обоего пола}. Будем считать, что рождения мальчика и рождение девочки – равновероятные события. Если рождение мальчика обозначить буквой М, а рождение девочки – Д, то пространство всех элементарных исходов состоит из четырех пар: . В этом пространстве лишь два исхода (МД и ДМ) отвечают событию B. Событие AB означает, что в семье есть дети обоего пола и старший ребенок – мальчик, это значит, что второй (младший) ребенок – девочка. Этому событию AB отвечает один исход – МД. Таким образом, |AB|=1, |B|=2 и

 

 

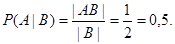
Задача 3. Мастер, имея 10 деталей, из которых 3 – нестандартных, берет и проверяет детали одну за другой, пока нему не попадется стандартная. Какова вероятность, что он проверит ровно две детали.

Решение. Событие А={мастер проверил ровно две детали} означает, что при такой проверке первая деталь оказалась нестандартной, а вторая – стандартная. Значит, , где ={ первая деталь оказалась нестандартной } и ={вторая деталь – стандартная}. Очевидно, что вероятность кроме того, (так как перед взятием второй детали у мастера осталось 9 деталей, из которых только 2 нестандартные и 7 стандартных). По теореме умножения

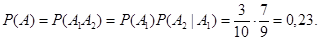
Событие А не зависит от В, если появление события В не меняет значения вероятности события А, т.е. условная вероятность равна безусловной: Р(А/В) = Р(А). Аналогично определяется независимость события B от A. Оказывается, что свойство независимости на самом деле симметрично относительно событий A и B, и потому определение независимости двух событий принимает более простой вид:

два события A и B независимы, если справедливо равенство

Р(АВ) = Р(А) × Р(В).

Это равенство можно использовать также как удобный критерий независимости при практической проверке независимости двух событий.

Задача 4. В одном ящике 3 белых и 5 черных шаров, в другом ящике – 6 белых и 4 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут один белый шар, если из каждого ящика вынуто по одному шару.

Решение. Событие A={хотя бы из одного ящика вынут белый шар} можно представить в виде суммы , где события  и  означают выборку одного белого шара из первого и второго ящика соответственно. Вероятность вытащить белый шар из первого ящика равна , а вероятность вытащить белый шар из второго ящика . Кроме того, в силу независимости  и  имеем: . По теореме сложения получаем:

 

.

 

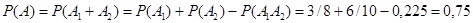Пусть событие А может быть реализовано только при условии появления одного из событий H_i, i = 1,..., n. Предположим, что события H_i несовместны, образуют полную группу (т.е. в результате испытания непременно произойдет одно из них) и вероятности их до опыта известны.. Такие события H_i называются гипотезами. Тогда вероятность события А можно вычислить с помощью формулы полной вероятности:

.

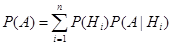Задача 5. Три экзаменатора принимают экзамен по некоторому предмету у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студента, а третий — 21 студентов (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, зато у третьего — 70%. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен.

Решение. Обозначим через 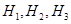 – гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи

 

, , .

 

Пусть событие A={слабо подготовившийся студент сдал экзамен}. Тогда снова в силу условия задачи

,  ,  .

Заключение

 

В заключении подведем основные итоги работы.

Итак, в работе были рассмотрены вероятность как событие, классическая вероятностная модель, аксиомы теории вероятности.

Опыт, эксперимент, наблюдение явления называются испытанием. Испытаниями, например, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенным на каждую грань числом очков — от одного до шести).

Результат (исход) испытания называется событием. Событиями являются: выпадение герба или выпадение цифры, попадание в цель или промах, появление того или иного числа очков на брошенной игральной кости.

Можно ли как-то измерить возможность появления некоторого случайного события? Другими словами, можно ли охарактеризовать эту возможность некоторым числом?

Всякое испытание влечет за собой некоторую совокупность исходов — результатов испытания, т. е. событий. Во многих случаях возможно перечислить все события, которые могут быть исходами данного испытания.

Определение 1. Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них.

Определение 2. События U₁, U₂,..., U, образующие полную группу попарно несовместимых и равновозможных событий, будем называть элементарными событиями.

Определение 3. Событие А называется благоприятствующим событию Б, если наступление события А влечет за собой наступление события В.

Определение 4 (классическое определение вероятности). Вероятностью Р(А) события А называется отношение m/n числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т. е. Р(А) = m/n.

Из приведенного классического определения вероятности вытекают следующие ее свойства.

1. Вероятность достоверного события равна единице.

Действительно, достоверному событию должны благоприятствовать все n элементарных событий, т.е. m = n, и, следовательно,

 

 

2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т.е. m = 0, откуда

 

 

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

 

Список литературы

 

1. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. М.: Наука, 1965.

2. Боровков А.А. Математическая статистика. М.: Наука, 1984.

3. Коршунов Д.А., Чернова Н.И. Сборник задач и упражнений по математической статистике. Новосибирск: Изд-во Института математики им. С.Л.Соболева СО РАН, 2001.

4. Феллер В. Введение в теорию вероятностей и ее приложения. М.: Мир, Т.2, 1984.

Поделиться:

Воспользуйтесь поиском по сайту: