 |
Расстояния между полями и силосными траншеями
|
|
|
|
Задание 1
Фермерское хозяйство, ориентированное на выращивание яровой пшеницы и овса, имеет  га пашни,
га пашни,  человеко-дней трудовых ресурсов и
человеко-дней трудовых ресурсов и 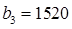 л топлива, которые используются в течение производственного цикла. Планируется реализовать выращенную продукцию из расчёта
л топлива, которые используются в течение производственного цикла. Планируется реализовать выращенную продукцию из расчёта  руб. с 1 га, засеянного пшеницей, и
руб. с 1 га, засеянного пшеницей, и  руб. с 1 га, засеянного овсом.
руб. с 1 га, засеянного овсом.
Технологические коэффициенты потребности в трудовых ресурсах и в топливе на 1 га в течение всего цикла приведены в табл.1.
Таблица 1
Использование трудовых ресурсов и расход топлива на 1 га
| Показатель | Яровая пшеница | Овёс |
| Трудовые ресурсы, чел.-дней | ||
| Топливо, л |
1. Составить экономико-математическую модель задачи при условии максимизации выручки от реализации продукции в конце цикла в виде задачи линейного программирования.
2. Решить поставленную задачу графическим способом.
3. Составить двойственную задачу.
4. Найти решение двойственной задачи по решению прямой задачи.
5. Определить дефицитность используемых ресурсов и их оценку полезности.
6. Определить для каждой культуры, выгодно ли её выращивать.
Решение. 1) Определим переменные задачи. Пусть  , га – площадь пашни, засеянная яровой пшеницей;
, га – площадь пашни, засеянная яровой пшеницей;  , га – площадь пашни, засеянная овсом. Составим ограничения на использование ресурсов: пашни, трудовых ресурсов и топлива.
, га – площадь пашни, засеянная овсом. Составим ограничения на использование ресурсов: пашни, трудовых ресурсов и топлива.
а) Площадь пашни, засеянная культурами, составит  га. Ограничение на использование пашни:
га. Ограничение на использование пашни:  . б) Общее использование трудовых ресурсов за цикл равно
. б) Общее использование трудовых ресурсов за цикл равно  человеко-дней. Ограничение по использованию трудовых ресурсов за цикл:
человеко-дней. Ограничение по использованию трудовых ресурсов за цикл:  . в) Суммарное потребление топлива за цикл равно
. в) Суммарное потребление топлива за цикл равно  л. Ограничение на потребление топлива:
л. Ограничение на потребление топлива:  .г) Суммарная выручка
.г) Суммарная выручка  от реализации яровой пшеницы и овса составит:
от реализации яровой пшеницы и овса составит: 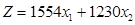 .
.
|
|
|
Учитывая условие максимизации выручки, получим задачу линейного программирования:
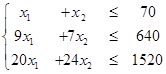
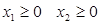
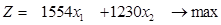
2) Решим полученную задачу линейного программирования графически.
а) Найдём область допустимых решений как пересечение решений неравенств системы условий. Решения неравенств и ОДР представим на рис. 1. Решаем первое неравенство:  . Граница решения этого неравенства описывается уравнением:
. Граница решения этого неравенства описывается уравнением:  . Это уравнение прямой. Обозначим её
. Это уравнение прямой. Обозначим её  . Построим
. Построим  по двум точкам. Прямая
по двум точкам. Прямая  проходит через точки:
проходит через точки:  и
и  (см. рис. 1). Определим искомую область по контрольной точке. Возьмём точку
(см. рис. 1). Определим искомую область по контрольной точке. Возьмём точку  . Подставим её координаты в первое неравенство:
. Подставим её координаты в первое неравенство:  . Отношение такое же, как и у неравенства. Решение первого неравенства содержит точку
. Отношение такое же, как и у неравенства. Решение первого неравенства содержит точку 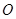 .
.
Решим аналогичным образом второе и третье неравенства
Определяем ОДР: ОДР =  (см. рис. 1).
(см. рис. 1).
б) Построим линию уровня и градиент. В качестве линии уровня для целевой функции  выберем прямую, проходящую через точку
выберем прямую, проходящую через точку  . Эта линия уровня – прямая, в уравнении которой, правая часть равна:
. Эта линия уровня – прямая, в уравнении которой, правая часть равна:  =
=  = 1554∙50 +1230∙0 =77700. Тогда уравнение линии уровня имеет вид:
= 1554∙50 +1230∙0 =77700. Тогда уравнение линии уровня имеет вид:  .
.
Координаты градиента целевой функции Z равны коэффициентам при переменных в целевой функции: 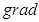
 . Так как размеры градиента не входят в рисунок, рассмотрим вектор, сонаправленный с градиентом, например,
. Так как размеры градиента не входят в рисунок, рассмотрим вектор, сонаправленный с градиентом, например,  =
= 
 (см. рис. 1).
(см. рис. 1).
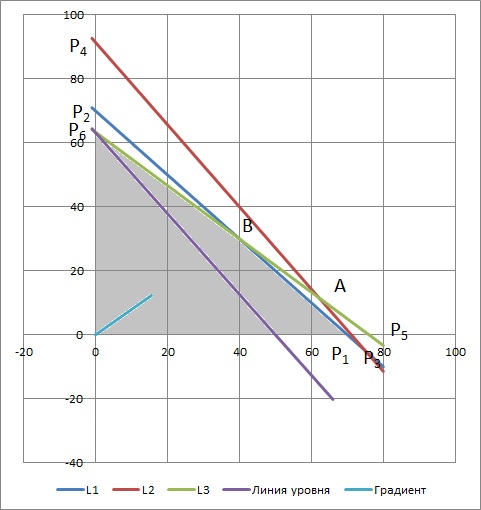

в) Определим решение задачи, передвигая линию уровня в направлении градиента. Решением будет точка  – точка пересечения прямых
– точка пересечения прямых  и
и  . Получаем
. Получаем  . Оптимальное решение:
. Оптимальное решение:  =
=  =(70;0).
=(70;0).
Тогда  =
=  = 1554∙70 +1230∙0 =108780. Итак, решение исходной задачи:
= 1554∙70 +1230∙0 =108780. Итак, решение исходной задачи:  = (70;0),
= (70;0),  = 108780
= 108780
3) Строим двойственную задачу, используя правила составления двойственной задачи. Учтём, что число переменных двойственной задачи равно трём, а число ограничений двум.
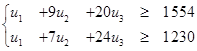
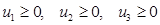
 .
.
4) Найдём решение двойственной задачи, используя вторую теорему двойственности. Для этого найдём остатки ресурсов при оптимальном плане  , которые обозначим переменными
, которые обозначим переменными 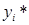 ,
,  = 1, 2, 3.
= 1, 2, 3.  =70–70–0=0;
=70–70–0=0; 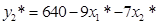 =640–9∙70–7∙0=10;
=640–9∙70–7∙0=10;  =1520–20∙70– 24∙0=120.
=1520–20∙70– 24∙0=120.
|
|
|
Проверим условия второй теоремы двойственности:  =0:
=0:  =70≠0→
=70≠0→ 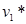 = 0 →
= 0 →  = 1554.
= 1554.  = 0:
= 0:  = 0 →
= 0 → 
 0 →
0 → 
 1230.
1230.  =0:
=0:  =0→
=0→  ;
;  =0:
=0:  =10→
=10→  ;
; 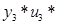 =0:
=0:  =120 →
=120 → 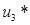 =0.
=0.
Из проверки этих условий получаем для двойственной задачи:
 = 1554,
= 1554, 
 1230,
1230,  = 0.
= 0.  = 0
= 0
Получили уравнение для вычисления значений  :
:  . Тогда оптимальное решение двойственной задачи:
. Тогда оптимальное решение двойственной задачи:  = (1554;0;0), Вычислим минимальное значение целевой функции двойственной задачи:
= (1554;0;0), Вычислим минимальное значение целевой функции двойственной задачи:  =
=  . Оптимальные значения функций обеих задач равны. Решение двойственной задачи:
. Оптимальные значения функций обеих задач равны. Решение двойственной задачи:  = (1554;0;0),
= (1554;0;0),  = (0;1),
= (0;1),  =108780.
=108780.
5) Так как  = 10 ≠ 0, то трудовые ресурсы используются не полностью и являются избыточным ресурсом. Так как
= 10 ≠ 0, то трудовые ресурсы используются не полностью и являются избыточным ресурсом. Так как  = 120 ≠ 0, то топливо используются не полностью и являются избыточным ресурсом. Оценка полезности посевных площадей
= 120 ≠ 0, то топливо используются не полностью и являются избыточным ресурсом. Оценка полезности посевных площадей  = 1554 ≠ 0. Тогда посевные площади являются дефицитными ресурсами, их дополнительное использование эффективно.
= 1554 ≠ 0. Тогда посевные площади являются дефицитными ресурсами, их дополнительное использование эффективно.
6) Так как посевные площади  = 70 ≠ 0 и
= 70 ≠ 0 и  = 0, то яровую пшеницу выращивать выгодно, а овёс невыгодно
= 0, то яровую пшеницу выращивать выгодно, а овёс невыгодно
Задание 2.
Планируется инвестирование трёх проектов на ближайшие три года. Размер инвестиций составляет  = 4 млн. руб. Размеры инвестиций каждого проекта кратен 800 тыс.руб. Размер инвестиций в количестве
= 4 млн. руб. Размеры инвестиций каждого проекта кратен 800 тыс.руб. Размер инвестиций в количестве  млн. руб., распределяемый в
млн. руб., распределяемый в  - ый проект, приносит по истечении трёх лет прибыль
- ый проект, приносит по истечении трёх лет прибыль  ,
,  =1, 2, 3. Функции
=1, 2, 3. Функции  заданы таблично (табл. 5).
заданы таблично (табл. 5).
Таблица 5
 тыс. руб. тыс. руб.
| 
| 
| 
| 
|

| ||||

| ||||

| ||||

| ||||

|
Предполагается, что: а) прибыль не зависит от инвестированных средств, вложенных в другие проекты; б) прибыль от инвестирования проектов выражается в тыс. руб.;
в) суммарная прибыль равна сумме прибылей, полученных от инвестирования каждого проекта.
Определить такие размеры инвестиций каждого проекта, чтобы суммарная прибыль от инвестирования всех проектов была наибольшей.
Рассмотреть вопрос о перераспределении инвестиций, если намечается инвестировать также четвёртый проект, прибыль от которых определяется функцией  , которая также задана таблично (табл. 14).
, которая также задана таблично (табл. 14).
Решение.Инвестировать проекты будем пошагово в порядке возрастания их номера, по очереди: на первом шаге 1 проект, на втором шаге второй проект, на третьем шаге третий проект. Определим следующие переменные и функции:  – количество нераспределённых средств, которые остались перед инвестированием на
– количество нераспределённых средств, которые остались перед инвестированием на  -ом шаге;
-ом шаге;  – количество средств, инвестированных в очередной проект на
– количество средств, инвестированных в очередной проект на  -ом шаге.
-ом шаге.
|
|
|
Тогда уравнением баланса для нераспределённых и распределенных средств на  -ом шаге будет
-ом шаге будет  . При этом учитывается условие, что
. При этом учитывается условие, что  .Уравнение перехода состояний на
.Уравнение перехода состояний на  -ом шаге имеет вид:
-ом шаге имеет вид:  .
.
Показатель эффективности  -ого шага
-ого шага  – прибыль, полученная по истечении трёх лет от инвестирования соответствующего проекта на
– прибыль, полученная по истечении трёх лет от инвестирования соответствующего проекта на  -ом шаге:
-ом шаге:  = =
= =  ;
; 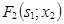 =
=  и
и  =
=  . Суммарная прибыль инвестирования трёх проектов равна:
. Суммарная прибыль инвестирования трёх проектов равна:  =
=  + +
+ + 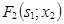 +
+  =
=  +
+  +
+  , которая должна быть максимальной.
, которая должна быть максимальной.
Определим функцию  – максимальная прибыль от инвестирования проектов на последних
– максимальная прибыль от инвестирования проектов на последних  шагах, начиная с
шагах, начиная с  -го года до 3-го года включительно, в предположении, что нераспределённые средства на оставшихся шагах, начиная с
-го года до 3-го года включительно, в предположении, что нераспределённые средства на оставшихся шагах, начиная с  -го года средства в дальнейшем распределялись оптимально. Тогда максимальная прибыль инвестирования на всех шагах, то есть всех проектов будет равна
-го года средства в дальнейшем распределялись оптимально. Тогда максимальная прибыль инвестирования на всех шагах, то есть всех проектов будет равна  =
=  .
.
Напишем реккурентные соотношения для вычисления функции  , используя уравнение Беллмана: 1) для последнего, 3-го шага
, используя уравнение Беллмана: 1) для последнего, 3-го шага  =
=  .
.
2) для  -го шага
-го шага  .
.
Найдём решение задачи на последнем – 3-м шаге. Запишем  в таблицу в третьем столбце. По определению
в таблицу в третьем столбце. По определению  =
=  . При этом
. При этом  =
= 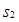 .
.
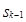
| 
| 
| 
|
| 131 | |||
| 231 | |||
| 321 | |||
| 401,2 | |||
| 651 | 492 |
Найдём решение задачи 2-м шаге:  . Учтём, что
. Учтём, что  . Тогда
. Тогда  . Последовательно вычислим
. Последовательно вычислим  при
при 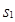 =0,1,2,3,4,5.
=0,1,2,3,4,5.  =
=  =
=  =0, при
=0, при  = 0.
= 0.
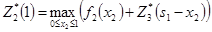 =
=  =
=
=  =13, при
=13, при  = 1.
= 1.
 =
=  =
=
= 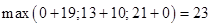 , при
, при  = 1.
= 1.
 =
=  =
=  , при
, при  = 1.
= 1.
 =
=  , при
, при  = 1,2.
= 1,2.
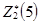 =
= 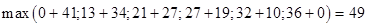 , при
, при  = 2.
= 2.
В столбце для функции  запишем найденные значения и в верхнем правом углу пометим значения
запишем найденные значения и в верхнем правом углу пометим значения  .
.
Найдём решение задачи на первом шаге для  млн.руб. по формуле
млн.руб. по формуле  .
.
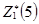 =
=  при
при  = 1.
= 1.  = 65 тыс. руб.
= 65 тыс. руб.
Выпишем оптимальные управления каждого шага: 1)  =1,
=1, 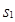 =
=  =
=  = 4;
= 4;  = 1,
= 1, 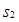 =
=  =1= 3;
=1= 3;  =
= 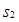 =3.
=3.
Ответ:  =(1; 1; 3);
=(1; 1; 3);  =65 тыс. руб.
=65 тыс. руб.
Рассмотрим вопрос, как перераспределятся инвестиции, если нужно будет ещё инвестировать ещё четвёртый проект, прибыль от которых определяется функцией  .
.
Перенумеруем шаги, на которых будем инвестировать проекты, положив, что на первом шаге инвестируется новый, четвёртый, проект, на втором шаге первый проект, на третьем шаге – второй, на четвёртом – третий. Тогда  будет максимальным значением прибыли от инвестирования третьего проекта на четвёртом шаге в размере
будет максимальным значением прибыли от инвестирования третьего проекта на четвёртом шаге в размере  ,
,  – значением прибыли от инвестирования второго и третьего проектов на третьем и четвёртом шагах в размере
– значением прибыли от инвестирования второго и третьего проектов на третьем и четвёртом шагах в размере 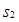 ,
,  – значением прибыли от инвестирования первого, второго и третьего проектов на втором, третьем и четвёртом шагах в размере
– значением прибыли от инвестирования первого, второго и третьего проектов на втором, третьем и четвёртом шагах в размере 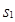 ,
,  – значением прибыли от инвестирования четвёртого, первого, второго и третьего проектов на первом, втором, третьем и четвёртом шагах в размере
– значением прибыли от инвестирования четвёртого, первого, второго и третьего проектов на первом, втором, третьем и четвёртом шагах в размере  . Значение
. Значение  при
при 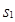 =4 млн. руб. уже найдено, определим значения
=4 млн. руб. уже найдено, определим значения  при
при 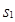 =0, 1, 2, 3 и 4 млн. руб.
=0, 1, 2, 3 и 4 млн. руб.
|
|
|
Найдём решение поставленной задачи на 2-м шаге. Определим значения функции  при
при 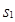 =0, 1, 2, 3, 4, а также оптимальные значения управления
=0, 1, 2, 3, 4, а также оптимальные значения управления  на втором шаге.
на втором шаге.
 =
=  =0, при
=0, при  = 0.
= 0.
 =
=  , при
, при  = 1.
= 1.
 =
= 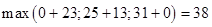 , при
, при  = 1.
= 1.
 =
=  , при
, при  = 1.
= 1.
 =
=  , при
, при  = 1.
= 1.
Находим решение поставленной задачи на первом шаге для  млн. руб. по формуле
млн. руб. по формуле
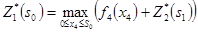 .
.
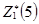 =
=  , при
, при  = 1.
= 1.  =77 тыс. руб.
=77 тыс. руб.
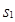
| 
| 
| 
| 
|
| 251 | 131 | |||
| 381 | 231 | |||
| 481 | 321 | |||
| 571 | 401,2 | |||
| 771 | 651 | 492 |
Выписываем оптимальные управления каждого шага: 1)  =1,
=1, 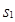 =
=  =
=  =4;
=4;  =1,
=1, 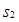 =
=  =
=  =3;
=3;  =2,
=2,  =
=  =
=  =1;
=1; 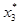 =
=  =1
=1
Ответ.  =(1; 2; 1; 1);
=(1; 2; 1; 1);  =77 тыс. руб.
=77 тыс. руб.
Задание 3
Планируется деятельность двух отраслей производства на 5 лет по использованию данного вида ресурса. Начальный объём ресурса, распределяемый между отраслями, равен  = 20000 руб. Количество ресурса
= 20000 руб. Количество ресурса  , распределённое в первую отрасль в начале года, даёт в конце года прибыль
, распределённое в первую отрасль в начале года, даёт в конце года прибыль  млн. руб. и возвращается в размере
млн. руб. и возвращается в размере  тонн. Аналогично для второй отрасли, функция прибыли
тонн. Аналогично для второй отрасли, функция прибыли  млн. руб., а возврата
млн. руб., а возврата  тонн. Количество распределенного ресурса в первую отрасль по технологическим причинам не может быть меньше
тонн. Количество распределенного ресурса в первую отрасль по технологическим причинам не может быть меньше  =1000 тонн, а во вторую отрасль – не менее
=1000 тонн, а во вторую отрасль – не менее  =2000 тонн.
=2000 тонн.
В конце года все возвращённые ресурсы заново распределяются между обеими отраслями. Новые ресурсы не поступают, прибыль в производство не вкладывается.
Требуется распределить имеющееся количество ресурса между двумя отраслями производства в течении пяти лет, чтобы суммарная прибыль от обеих отраслей за эти 5 лет была максимальной.
Решение. Представим процесс распределения ресурса в виде многошагового процесса управления. Определим следующие переменные:  – количество средств, которые распределяются в начале
– количество средств, которые распределяются в начале  -го года;
-го года;  – количество средств, выделенных 1-ой отрасли в
– количество средств, выделенных 1-ой отрасли в  -ом году;
-ом году; 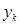 – количество средств, выделенных 2-ой отрасли в
– количество средств, выделенных 2-ой отрасли в  -ом году. Уравнением баланса для распределённых средств в
-ом году. Уравнением баланса для распределённых средств в  -ом году будет
-ом году будет  . Из этого соотношения можно выразить переменную
. Из этого соотношения можно выразить переменную 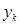 через
через  и
и  :
:  . Учтём условия на минимальную норму распределения ресурса по отраслям:
. Учтём условия на минимальную норму распределения ресурса по отраслям:  и
и  . Получаем, что
. Получаем, что  .
.
|
|
|
Составим уравнение перехода состояний в  -ом году, учитывая возврат ресурса в отраслях:
-ом году, учитывая возврат ресурса в отраслях:  =
=  +
+  – количество средств, вернувшихся в конце
– количество средств, вернувшихся в конце  -ого года. Так как
-ого года. Так как  , выражаем
, выражаем  через
через  и
и  :
:  =
=  =
=  .
.
Определим показатель эффективности  -ого шага – прибыль, полученная в течении
-ого шага – прибыль, полученная в течении  -ого года от обеих отраслей:
-ого года от обеих отраслей:  . Выразим
. Выразим 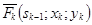 через
через  и
и  :
:  =
= 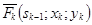 =
=  =
= 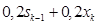 .
.
Суммарная прибыль за 5 лет равна:  =
=  =
=  = =
= =  , которая должна быть максимальной.
, которая должна быть максимальной.
Мы представили задачу распределения ресурса между отраслями как задачу динамического программирования. Решим поставленную задачу, используя методы динамического программирования.
Определим условно-оптимальную функцию  – максимальная прибыль, полученная от использования ресурса отраслями, за последние
– максимальная прибыль, полученная от использования ресурса отраслями, за последние  лет, начиная с
лет, начиная с  -го года и до
-го года и до 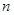 -го года включительно, в предположении, что ресурс, имеющийся на начало
-го года включительно, в предположении, что ресурс, имеющийся на начало  -го года в количестве
-го года в количестве  , в последующие годы распределялся оптимально.
, в последующие годы распределялся оптимально.
По определению максимальная прибыль за 5 лет будет равна  =
= 
Напишем рекуррентные соотношения для вычисления функции  , используя уравнение Беллмана: 1) для последнего,
, используя уравнение Беллмана: 1) для последнего, 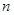 -го шага
-го шага  ;
;
2) для  -го шага
-го шага  .
.
Найдём решение задачи на последнем (5-ом) шаге:  =
=  . Так как коэффициент при
. Так как коэффициент при  , равный 0,2, положительный, то функция
, равный 0,2, положительный, то функция 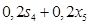 достигает максимума при наименьшем значении переменной
достигает максимума при наименьшем значении переменной  :
:  =
=  . Тогда значение функции
. Тогда значение функции  равно:
равно: 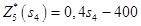
Найдём решение задачи на 4-ом шаге. Условно-оптимальная функция третьего шага равна:  =
= 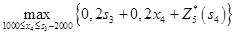 . Подставим
. Подставим 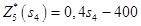 ;
;  . По формуле перехода состояний
. По формуле перехода состояний  . Тогда
. Тогда  Найдём максимум функции
Найдём максимум функции  . Он достигается при
. Он достигается при  =
= 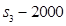 , так как коэффициент при
, так как коэффициент при  , равный 0,16, положительный. Получаем значение функции
, равный 0,16, положительный. Получаем значение функции 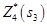 :
: 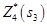 =
= 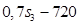
Решение задачи для 3-го шага:  =
=  =
=
=  . Так как
. Так как  =
= 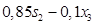 , тогда
, тогда
 =
=  =
=  .
.
Найдём максимум функции  . Он достигается при
. Он достигается при 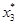 =
= 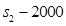 , так как коэффициент при
, так как коэффициент при 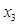 , равный 0,13, положительный. Получаем значение функции
, равный 0,13, положительный. Получаем значение функции  :
: 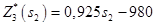
Решение задачи для 2-го шага:  =
= 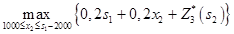 =
=
= 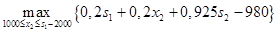 . Так как
. Так как  =
=  , тогда
, тогда  =
=  =
=  .
.
Найдём максимум функции  . Он достигается при
. Он достигается при
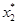 =
=  , так как коэффициент при
, так как коэффициент при  , равный 0,1075, положительный. Получаем значение функции
, равный 0,1075, положительный. Получаем значение функции  :
:  =
= 
Найдём решение задачи на 1-ом шаге:  =
=  . Подставим
. Подставим  =
=  :
:
 =
=  . Так как
. Так как  =
=  , тогда
, тогда  =
=  =
=
= 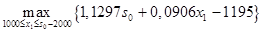
 =
=  . Тогда
. Тогда  =
=  .
.
Так как  =
=  = 20000, то
= 20000, то  =
=  руб.
руб.
Выпишем оптимальные управления каждого шага:  =18000,
=18000, 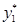 =2000
=2000
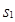 =
=  .
.  =13200,
=13200,  =2000.
=2000. 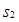 =
=  =11600.
=11600. 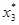 = 9600,
= 9600,  =2000.
=2000.  =
=  =8900.
=8900.  =7900,
=7900,  =2000.
=2000.  =
=  =6775.
=6775.  =4775,
=4775,  =2000
=2000
Ответ.  =(18000; 13200; 9600; 7900; 4775);
=(18000; 13200; 9600; 7900; 4775);  =(2000; 2000; 2000; 2000; 2000);
=(2000; 2000; 2000; 2000; 2000);  =23029,8 руб.
=23029,8 руб.
Контрольная работа №2
Задание 1
В хозяйстве необходимо за время уборки при заготовке силоса перевезти 4000 т зелёной массы с пяти поля к четырём силосным траншеям. Зелёная масса каждого поля равна: А1 =400, А2 =800, А3 =600, А4 =1200, А5 =1000 т; вместимости силосных траншей равны: В1 =800, В2 = 1600, В3 =1000, В4 =600 т. Оплата за тонну зелёной массы, перевозимую с полей к силосным траншеям, приведена в табл. 15.
Таблица 15
Расстояния между полями и силосными траншеями
| Поля | Силосные траншеи | |||
| 1-ый | 2-ой | 3-ий | 4-ый | |
| 1-е | ||||
| 2-е | ||||
| 3-е | ||||
| 4-е | ||||
| 5-е |
Составить такой план перевозок, чтобы суммарные транспортные затраты были минимальными. Опорный план найти методом наименьшего элемента. Оптимальный план найти методом потенциалов.
Решение. Проверим баланс между общим объёмом А зелёной массы, вывозимой с полей и суммарной вместимостью В всех силосных траншей. A = a1+a2+a3+a4+a5=400+800+600 +1200+1000 = 4000, В = b1+b2+b3+b4 =800+1600+1000+600 =4000. Так как А = В, то задача является закрытой.
Определим опорный план методом наименьшего элемента. Среди стоимостей за перевозку зелёной массы с полей к силосным траншеям выберем наименьшую. Это стоимость перевозки между третьим полем и второй силосной траншеей с32=1. Поставим зелёную массу в клетку (3;2).
Объём поставки в эту клетку – минимум из остатков объёма зелёной массы 3 поля и вместимости 2 силосной траншеи. Так как зелёная масса ещё не распределялась, то ос
|
|
|


