 |
Непрерывность функции нескольких переменных
|
|
|
|
По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой точке равен ее значению в ней:
(1)
Условие непрерывности f в точке (х0, у0) можно записать в эквивалентной форме:
(1')
т.е. функция f непрерывна в точке (х0, у0), если непрерывна функция f (х0 + Δх, у0 + Δу) от переменных Δх, Δу при Δх = Δу = 0.
Можно ввести приращение Δи функции и = f (x, y) в точке (x, y), соответствующее приращениям Δх, Δу аргументов
Δи = f (х + Δх, у + Δу) – f (x, y)
и на этом языке определить непрерывность f в (x, y): функция f непрерывна в точке (x, y), если
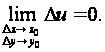(1'')
Теорема. Сумма, разность, произведение и частное непрерывных в точке (х0, у0) функций f и φ есть непрерывная функция в этой точке, если, конечно, в случае частного φ (х0, у0) ≠ 0.
Постоянную с можно рассматривать как функцию f (x, y) = с от переменных x, y. Она непрерывна по этим переменным, потому что
| f (x, y) – f (х0, у0) | = |с – с | = 0 0.
Следующими по сложности являются функции f (x, y) = х и f (x, y) = у. Их тоже можно рассматривать как функции от (x, y), и при этом они непрерывны. Например, функция f (x, y) = х приводит в соответствие каждой точке (x, y) число, равное х. Непрерывность этой функции в произвольной точке (x, y) может быть доказана так:
| f (х + Δх, у + Δу) – f (x, y) | = | f (х + Δх) – х | = | Δх | ≤ 
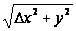0.
Если производить над функциями x, y и постоянными действия сложения, вычитания и умножения в конечном числе, то будем получать функции, называемые многочленами от x, y. На основании сформулированных выше свойств многочлены от переменных x, y – непрерывные функции от этих переменных для всех точек (x, y) 
R2.
|
|
|
Отношение P/Q двух многочленов от (x, y) есть рациональная функция от (x, y), очевидно, непрерывная всюду на R2, за исключением точек (x, y), где Q (x, y) = 0.
Функция
Р (x, y) = х3 – у2 + х2у – 4
может быть примером многочлена от (x, y) третьей степени, а функция
Р (x, y) = х4 – 2х2у2 + у4
есть пример многочлена от (x, y) четвертой степени.
Приведем пример теоремы, утверждающей непрерывность функции от непрерывных функций.
Теорема. Пусть функция f (x, y, z) непрерывна в точке (x0, y0, z0) пространства R3 (точек (x, y, z)), а функции
x = φ (u, v), y = ψ (u, v), z = χ (u, v)
непрерывны в точке (u0, v0) пространства R2 (точек (u, v)). Пусть, кроме того,
x0 = φ (u0, v0), y0 = ψ (u0, v0), z0 = χ (u0, v0).
Тогда функция F (u, v) = f [ φ (u, v), ψ (u, v), χ (u, v) ] непрерывна (по
(u, v)) в точке (u0, v0).
Доказательство. Так как знак предела можно внести под знак характеристики непрерывной функции, то
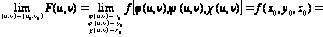
Теорема. Функция f (x, y), непрерывная в точке (х0, у0) и не равная нулю в этой точке, сохраняет знак числа f (х0, у0) в некоторой окрестности точки (х0, у0).
По определению функция f (x) = f (x1,..., хп) непрерывна в точке х0 = (х01,..., х0п), если она определена в некоторой ее окрестности, в том числе и в самой точке х0, и если предел ее в точке х0 равен ее значению в ней:
(2)
Условие непрерывности f в точке х0 можно записать в эквивалентной форме:
(2')
т.е. функция f (x) непрерывна в точке х0, если непрерывна функция f (х0 + h) от h в точке h = 0.
Можно ввести приращение f в точке х0, соответствующее приращению h = (h1,..., hп),
Δh f (х0) = f (х0 + h) – f (х0)
и на его языке определить непрерывность f в х0: функция f непрерывна в х0, если
(2'')
Теорема. Сумма, разность, произведение и частное непрерывных в точке х0 функций f (x) и φ (x) есть непрерывная функция в этой точке, если, конечно, в случае частного φ (х0) ≠ 0.
Замечание. Приращение Δh f (х0) называют также полным приращением функции f в точке х0.
|
|
|
В пространстве Rn точек х = (x1,..., хп) зададим множество точек G.
По определению х0 = (х01,..., х0п) есть внутренняя точка множества G, если существует открытый шар с центром в нем, полностью принадлежащий к G.
функций нескольких переменных" width="17" height="14" align="BOTTOM" border="0" /> Rn называется открытым, если все его точки внутренние.
Говорят, что функции
х1 = φ1 (t),..., хп = φп (t) (a ≤ t ≤ b)
непрерывные на отрезке [a, b], определяют непрерывную кривую в Rn, соединяющую точки х1 = (х11,..., х1п) и х2 = (х21,..., х2п), где х11 = φ1 (а),..., х1п = φп (а), х21 = φ1 (b),..., х2п = φп (b). Букву t называют параметром кривой.
Множество G называется связным, если любые его две точки х1, х2 можно соединить непрерывной кривой, принадлежащей G.
Связное открытое множество называется областью.
Теорема. Пусть функция f (x) определена и непрерывна на Rn (во всех точках Rn). Тогда множество G точек х, где она удовлетворяет неравенству
f (x) > с (или f (x) < с), какова бы ни была постоянная с, есть открытое множество.
В самом деле, функция F(x) = f(x) – с непрерывна на Rn, и множество всех точек х, где F(x) > 0, совпадает с G. Пусть х0 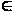G, тогда существует шар
| х – х0 | < δ,
на котором F(x) > 0, т.е. он принадлежит к G и точка х0 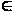G – внутренняя для G.
Случай с f (x) < с доказывается аналогично.
Таким образом, функция нескольких переменных f (М) называется непрерывной в точке М0, если она удовлетворяет следующим трем условиям:
а) функция f (М) определена в точке М0 и вблизи этой точки;
б) существует предел 
;
в) 
Если в точке М0 нарушено хотя бы одно из этих условий, то функция в этой точке терпит разрыв. Точки разрыв могут образовывать линии разрыва, поверхность разрыва и т. д. Функция f (М) называется непрерывной в области G, если она непрерывна в каждой точке этой области.
Пример 1. Найти точки разрыва функции: z = ln (x2 + y2).
Решение. Функция z = ln (x2 + y2) терпит разрыв в точке х = 0, у = 0. Следовательно, точка О (0, 0) является точкой разрыва.
Пример 2. Найти точки разрыва функции: 
Решение. Функция не определена в точках, в которых знаменатель обращается в нуль, т.е. x2 + y2 – z2 = 0. Следовательно, поверхность конуса
x2 + y2 = z2 является поверхностью разрыва.
|
|
|
