Проверка соответствия эмпирического распределения теоретическому

Содержание

 

Введение………………………………………………………………………1

1 Определение закона распределения вероятностей

результатов измерения ……………………………………………………..2

2 Проверка соответствия эмпирического распределения теоретическому.5

3 Заключение………………………………………………………………….7

4 Список использованных источников ……………………………………..8

Приложение А

 

 

Введение

 

В современной отечественной метрологии существует множество неотложных задач. Одна из таких проблем - недостаточная работа в сфере технологической стандартизации. Кроме того, направления работы по стандартизации и внедрению новых технологий бывают зачастую не связаны друг с другом.

Метрология в современном мире оказывает огромное влияние на развитие естественных и технических наук, поскольку увеличение точности измерений является одним из шагов к совершенствованию исследований природы, открытий и практического применения точных знаний. Для обеспечения научно-технического прогресса метрология должна опережать в своем развитии другие области науки и техники, так как метрология и уровень технологии являются неразрывно связанными понятиями, и для каждой из отраслей точные измерения являются одним из путей совершенствования.

Метрология связана практически со всеми отраслями науки и техники. Новое в метрологию привносится постоянно, так как эта отрасль очень мобильна и должна развиваться вслед за изменениями, происходящими в мире.

 

 

 

Определение закона распределения вероятностей результатов измерения

 

1.1 Ранжирование значений выборки Х в порядке возрастания и представления в виде вариационного ряда (приложение А):

X₁≤X₂≤…≤X_n (1)

1.2 Определение среднего арифметического значений выборки:

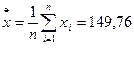(2)

1.3 Определение несмещенной оценки дисперсии:

(3)

1.4 Определение среднего квадратического отклонения результата измерения:

(4)

1.5 Определение четвертого центрального момента :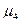

(5)

1.6 Определение контрэксцесса :

(6)

1.7 Исключение из выборки промахов. При этом исключаются значения х_i отличающиеся от среднего значения больше, чем 3

, (7)

Промах равен 0.

1.8 Определение оценки центра распределения

В качестве оценки я беру медиану, так как она используется для симметричных экспоненциальных распределений с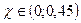

при не четном (8)

1.9 Определение оценок третьего центрального момента :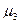

(9)

1.10 Определение коэффициента ассиметрии :

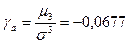(10)

1.11 Определение стандартного отклонения коэффициента ассиметрии :

(11)

1.12 Определение оценки симметричности распределения в соответствии с условием. Распределение можно считать симметричным, если выполняется условие. Распределение симметрично.

(12)

1.13 Определение эксцесса Э:

(13)

1.14 Определение коэффициента эксцесса:

(14)

1.15 Определение показателя формы. Показатель формы распределения

, связан с эксцессом э функциональной зависимостью.

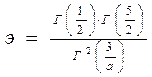(15)

1.15 Определение числа интервалов m:

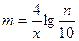или (16)

1.16 Определение ширины интервалов d:

(17)

1.17 Определение суммы частостей по всем интервалам W:

(18)

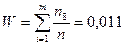
W=1

1.18 Определение энтропийного коэффициента k:

Энтропией случайной величины называется функция, заданная формулой:

H(Y) = - ∑Pj·log Pj, (19)

и характеризующая стандартное отклонение симметричного распределения.

Если эта величина близка к 0, то распределение симметрично.

 

1.19 Построение гистограммы показано на рисунке 1

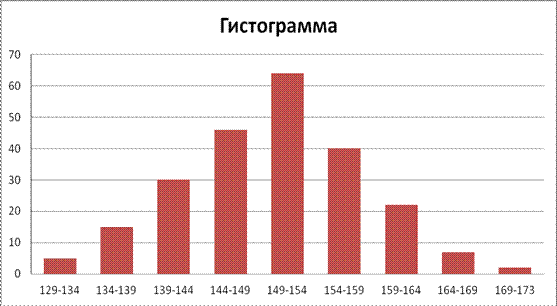
Рисунок 1 – Гистограмма

 

 

Проверка соответствия эмпирического распределения теоретическому

Критерий согласия Пирсона (χ²) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.

Статистикой критерия Пирсона служит величина

, (20)

где p_j - вероятность попадания изучаемой случайной величины в j-и интервал, вычисляемая в соответствии с гипотетическим законом распределением F(x).

При вычислении вероятности p_j нужно иметь в виду, что левая граница первого интервала и правая последнего должны совпадать с границами области возможных значений случайной величины. Например, при нормальном распределении первый интервал простирается до -∞, а последний - до +∞.

Нулевую гипотезу о соответствии выборочного распределения теоретическому закону F(x) проверяют путем сравнения вычисленной по формуле. величины с критическим значением χ²_α, найденным по таблице Лапласа для уровня значимости α и числа степеней свободы k = e ₁ - m - 1. Здесь e ₁ - число интервалов после объединения; m - число параметров, оцениваемых по рассматриваемой выборке. Если выполняется неравенство χ² ≤χ²_α,
то нулевую гипотезу не отвергают. При несоблюдении указанного неравенства

принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению.

Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ² другими критериями. Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100).

Проделав необходимые вычисления в Ms Excel составили следующую таблицу №1

Таблица 1- Проверка соответствия по критерию Пирсона

Qi	Qi+1	Zi	Zi+1	Ф(zi)	Ф(zi+1)	Pi	nPi	ni-nPi	(ni-nPi)^2/nPi
		-2,56469	-1,94692	-0,49477	-0,47381	0,02096	4,84176	0,15824	0,005171652
		-1,94692	-1,32915	-0,47381	-0,40824	0,06557	15,14667	-0,14667	0,001420252
		-1,32915	-0,71137	-0,40824	-0,26115	0,14709	33,97779	-8,97779	2,372158792
		-0,71137	-0,0936	-0,26115	-0,03586	0,22529	52,04199	-6,04199	0,701465166
		-0,0936	0,524171	-0,03586	0,19847	0,23433	54,13023	9,86977	1,799592572
		0,524171	1,141944	0,19847	0,37286	0,17439	40,28409	-0,28409	0,002003449
		1,141944	1,759717	0,37286	0,4608	0,08794	20,31414	-1,31414	0,085012899
		1,759717	2,377489	0,4608	0,49134	0,03054	7,05474	-0,05474	0,000424745
		2,377489	2,871708	0,49134	0,49801	0,00667	1,54077	0,45923	0,136874545

В результате вычислений получили следующие данные:

(21)

при к=6 и α=0,05 (22)

Соблюдается неравенство χ² ≤χ²_α, что означает, что гипотезу о нормальном распределении выборки не отвергают. Выборка распределена нормально

Заключение

Итак, проделав возможные вычисления с помощью Microsoft Exсel мы доказали нормальность распределения предоставленной выборки. Вариационный ряд симметричен, кривая распределения плосковершинная. Присутствует легкая асимметрия в левой части, однако в целом распределение симметрично.

 

Поделиться:

Воспользуйтесь поиском по сайту: