 |
Для переводного экзамена (по билетам)
|
|
|
|
1. Если две стороны и угол между ними одного треугольника равны 2. Средняя линия треугольника - отрезок, соединяющий
соответственно двум сторонам и углу между ними другого вершину треугольника с серединой противолежащей стороны.
треугольника, то такие треугольники равны. Медианы пересекаются в одной точке и делятся ей в отношении
2:1, считая от вершины. Медианы делят треугольник на 6 равновеликих.
Если сторона и прилежащие к ней углы одного треугольника Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам.
равны соответственно стороне и прилежащим к ней углам
другого треугольника, то такие треугольники равны.
(Пусть Δ ABC и  таковы, что
таковы, что 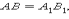
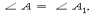
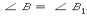 4. 1) точка пересечения биссектрис
4. 1) точка пересечения биссектрис
По аксиоме 4.1 существует 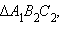 равный Δ ABC, с вершиной
равный Δ ABC, с вершиной 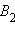 на луче
на луче 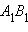 и 2) точка пересечения серединных перпендикуляров
и 2) точка пересечения серединных перпендикуляров
сторон треугольника
с вершиной 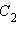 в той же полуплоскости, где и вершина
в той же полуплоскости, где и вершина 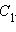 3) точка пересечения медиан
3) точка пересечения медиан
Так как  то вершина
то вершина 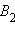 совпадает с вершиной
совпадает с вершиной  4) точка пересечения высот треугольника
4) точка пересечения высот треугольника
Так как  и
и 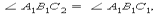 то луч
то луч 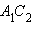 Точка лежит на серединном перпендикуляре к
Точка лежит на серединном перпендикуляре к
совпадает с лучом 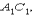 а луч
а луч 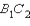 совпадает с лучом
совпадает с лучом 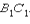 Отсюда следует, отрезку тогда и только тогда, когда она равноудалена
Отсюда следует, отрезку тогда и только тогда, когда она равноудалена
от концов этого отрезка.
что вершина 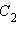 совпадает с вершиной
совпадает с вершиной 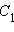 Итак,
Итак,  совпадает с треугольником
совпадает с треугольником
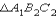 а значит, равен Δ ABC.
а значит, равен Δ ABC.
3. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
В равностороннем треугольнике высота является и биссектрисой, и медианой.
В равнобедренном треугольнике углы при основании равны.
5. Смежные à Сумма смежных углов равна 180; Если два смежных угла равны, то они прямые; Угол, смежный с тупым углом,
|
|
|
является острым и наоборот.
Вертикальные à Они равны и располагаются на продолжении сторон друг друга.
Центральный à Центральный угол окружности равен дуге, на которую он опирается; в два раза больше вписанного угла.
(углы) Вписанный à Равен половине центрального угла, опирающегося на ту же дугу, и равен половине дуги, на которую он опирается,
либо дополняет половину центрального угла до 180°.
Накрест-лежащие à Попарно равны.
Соответствующие à Попарно равны.
Односторонние à Сумма равна 180 градусов.
6. Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
В параллелограмме противоположные стороны равны и противоположные углы равны.
Диагонали параллелограмма точкой пересечения делятся пополам.
Углы, прилежащие к любой стороне, в сумме равны 180 градусов.
Диагонали параллелограмма делят его на два равных треугольника.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Т - Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD. Эти треугольники равны между собой по двум сторонам и углу между ними (BD - общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а, следовательно, угол3=угол4. А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.
|
|
|
7. Прямоугольником называется параллелограмм, у которого все углы прямые. Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма.
8. Прямоугольником называется параллелограмм, у которого все углы прямые. Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма.
9. Касательная к окружности — прямая, имеющая с окружностью единственную общую точку
Т -Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна этому радиусу, то она является касательной.
Свойство касательной. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Признак касательной. Прямая, проходящая через точку окружности и перпендикулярная к радиусу, проведенному в эту точку, является касательной.
10. Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны.
Квадрат - все углы квадрата — прямые, все стороны квадрата — равны. Диагонали квадрата равны и пересекаются под прямым углом. Диагонали квадрата делят его углы пополам.
Т -Диагонали ромбапересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам.
11. Если все стороны треугольника касаются окружности, то окружность называется вписанной в треугольник, а треугольник - описанным около этой окружности.
Т -Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
12. Если катеты одного треугольника соответственно равны катетам другого треугольника, то такие прямоугольные треугольники равны. Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны.
У прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы.
Т -Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.
Дано: 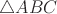 и
и 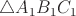 ,
, 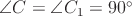 ,
,  ,
,  .
.
Требуется доказать: 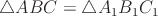 .
.
Доказательство:
Доказываем наложением 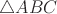 на
на 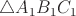 . Гипотенузы при этом совместятся.
. Гипотенузы при этом совместятся. 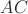 пойдёт по
пойдёт по 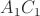 , так как
, так как  . Но
. Но 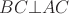 и
и 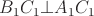 .
.  совпадёт с
совпадёт с  .
.
|
|
|
13-14 были на последних уроках и их не трудно вспомнить
15. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности
Если две хорды окружности, пересекаются в одной точке, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Т -Квадрат касательной равен произведению секущей на её внешнюю часть.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Это все вопросы, предоставленные в документе (кроме тех, которые мы всё-ещё используем). Достаточно распечатать, повторить и вы готовы к сдаче!
|
|
|


