 |
Дифференциал независимой переменной
|
|
|
|
ТЕМА 3.1. ПРОИЗВОДНАЯ
Производная
Пусть функция у = f (x) определена и непрерывна на (a, b), пусть x 0 Î (a, b). Дадим в точке х 0 приращение аргументу D х так, что точка х 0 +D х Î (a, b). Тогда функция получит соответствующее приращение D у = f (x 0+D x)- f (x 0).
Определение 3.1. Производной функции в данной точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, если этот предел существует и конечен. Функция называется дифференцируемой в точке х 0.

Определение 3.2. Функция называется дифференцируемой на множестве А Ì R, если она дифференцируема в каждой точке множества А.
Геометрический смысл производной
Определение 3.3. Касательной к плоской кривой называется предельное положение секущей, когда вторая точка пересечения неограниченно приближается по кривой к первой точке (рис. 3.1).

Рис. 3.1.
Пусть функция у = f (x) определена и непрерывна на (a, b), x 0 Î (a, b).
Дадим приращение аргументу D х так, что точка х 0 + D х Î (a, b). Функция получит приращение
D у = f (x 0+D x)- f (x 0).
Проведем секущую к графику (рис. 3.2) через точки А (х 0, f (x 0)), В (x 0+D x, f (x 0+D x)).

Рис. 3.2
Рассмотрим DABC;

При ∆ x ® 0 A ® B, секущая стремится к касательной, a ® j, tga ® tgj,
Переходя к пределу при ∆ x ® 0 в равенстве  получим
получим
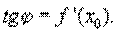
Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в данной точке.
Связь между непрерывностью
и дифференцируемостью функции
Теорема 3.1. (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке, то она непрерывна в этой точке.
Доказательство. Пусть функция у = f (x)дифференцируема в точке х 0. Дадим в этой точке аргументу приращение D х. Функция получит приращение D у. Найдем
|
|
|


Следовательно, у = f (x)непрерывна в точке х 0.
Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.
Следствие. Если х 0 ¾ точка разрыва функции, то в ней функция не дифференцируема.
Пример 3.1. у = |х|, х 0=0.



В точке х 0=0функция непрерывна, но производной не существует.
Свойства производных
Теорема 3.2. Производная постоянной функции равна нулю.
Доказательство. f (x)= c, "x 0D y = f (x 0+D x)- f (x 0)= c - c = 0,

Теорема 3.3. Если функции u, v, w дифференцируемы в некоторой точке, то и их алгебраическая сумма также дифференцируема в этой точке, причем производная алгебраической суммы равна алгебраической сумме производных и выполняется равенство

Теорема 3.3. Если функции u и v дифференцируемы в некоторой точке, то и их произведение также дифференцируемо в этой точке, причем выполняется равенство

Следствие. Постоянный множитель можно выносить за знак производной.

Теорема 3.3. Если функции u и v дифференцируемы в некоторой точке и функция v в этой точке отлична от нуля, то существует производная частного в этой точке, причем

Производные от элементарных функций
Справедливы следующие формулы:

Пример 3.1. Найти производные функции:
а) y = 2 x 5 – 5 × 2 x + 4 x – 7log2 x – ln 2;
б) y = (1 + x 2) × arctg x;
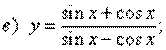
Решение:
а) Используя правила дифференцирования, получим:
y' = (2 x 5) ' – (5 × 2 x) ' + (4 x) ' – (7log2 x) ' – (ln 2) ' =
= 2 × (x 5) ' – 5 × (2 x) ' + 4 (x) ' – 7 × (log2 x) ' – 0 =

б) Используя правила дифференцирования, получим:
y' = (1 + x 2) ' × arctg x + (1 + x 2) ' × (arctg x) ' =

в) Используя правила дифференцирования, получим:

Дифференциал
Определение 3.3. Главная линейная относительно D х часть малого приращения функции называется дифференциалом функции и обозначается dy.
Если приращение функции можно представить в виде ∆ y = k ∆ x +a(x), где a(∆ x) ¾ б. м. функция более высокого порядка, чем D х при ∆ x ®0
|
|
|

dy = k ∆ x.
Пример 3.2. y = x 2.


Теорема 3.8. Функция не может иметь двух различных дифференциалов.
Дифференциал независимой переменной
Рассмотрим функцию у = х, dy = dx. Из теорем о связи производной и дифференциала следует, что:
dy = 1 × D x,
dx = dy = D x.
Дифференциал независимой переменной равен малому приращению этой переменной.
Таким образом, получена формула для вычисления дифференциала функции:
dy = f ¢(x 0) dx.
Дифференциал функции равен произведению производной функции в данной точке на дифференциал независимой переменной.

Пример 3.3 Найти среднюю скорость движения тела, совершаемого по закону S = 6 t 2 + 1, для промежутка времени от t 1 = 1 до t 2 = 3.
План решения
1. Найти мгновенную скорость v (t) = S' (t) в момент времени t, воспользовавшись формулами:
1. (u ± v) ' = u' ± v';
2. (Cu) ' = Cu', C = const;
3. C' = 0.
3. (xn) ' = nxn – 1.
2. Найти значение скорости в момент времени t 1 и t 2, т.е. v (t 1) и v (t 2).
3. Найти среднее значение скорости.
Решение
v (t) = S' (t) = (6 t 2 + 1) ' = (6 t 2) ' + 1 ' = 12 t.
v (t 1) = v (1) = 12 · 1 = 12.
v (t 2) = v (3) = 12 · 3 = 36.
.
vср. = 23.
|
|
|


