 |
Определение токов методом контурных токов
|
|
|
|
ПоРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Упростить схему;
2. Составить на основании законов Кирхгофа систему уравнений;
3. Определить токи во всех ветвях схемы методом контурных токов;
4. Определить токи во всех ветвях схемы методом узловых напряжений;
5. Результаты расчёта токов, проведённого двумя методами, свести в таблицу и сравнить между собой;
6. Составить баланс мощностей.
Схематическое изображение анализируемой электрической цепи и значения сопротивлений и ЭДС представлены ниже на рисунке 1 и в таблице 1, соответственно.
 |
Рисунок 1 – Графическое представление анализируемой цепи
Таблица 1 – Таблица значений сопротивлений и ЭДС элементов цепи
 |
| R1 | R2 | R3 | R’4 | R”4 | R5 | R’6 | R”6 | E2 | E3 |
| 19,5 Ом | 7,5 Ом | 13,5Ом | 21 Ом | 21 Ом | 15 Ом | 4Ом | 2 Ом | 21 В | 45В |
1 
упростить схему
Упростим электрическую схему, представленную на рисунке 1, заменив последовательно и параллельно соединённые резисторы четвёртой и шестой ветвей эквивалентными.
Рисунок 2 – Графическое представление эквивалентной цепи
Таким образом, получим эквивалентную электрическую схему (рисунок 2) со следующими значениями эквивалентных сопротивлений четвертой и шестой ветвей:
Для простоты дальнейших вычислений составим таблицу значений сопротивлений и ЭДС эквивалентной электрической цепи (таблица 2).
Таблица 2 - Таблица значений сопротивлений и ЭДС эквивалентной цепи
| R1 | R2 | R3 | R4 | R5 | R6 | E2 | E3 |
| 19,5 Ом | 7,5 Ом | 13,5 Ом | 10,5 Ом | 15 Ом | 6 Ом | 21 В | 45 В |
Расчет токов по законам кирхгофа
Первый закон Кирхгофа гласит: алгебраическая сумма токов, входящих в любой узел любой электрической цепи, с учетом того, что значения вытекающих токов берутся с обратным знаком, равна нулю.
|
|
|
(1)
Второй закон Кирхгофа гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Слагаемые, включающие ток или ЭДС, текущие противоположно направлению произвольно выбранного обхода контура, берутся с обратным знаком.
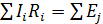(2)
Первоначально, рассчитаем количество уравнений, необходимых для определения значений всех токов анализируемой цепи по правилам Кирхгофа. Общее количество необходимых уравнений равно количеству неизвестных токов или количеству ветвей, носящих неизвестные токи. Таким образом, общее количество уравнений N = 6.
(3)
где p - количество ветвей, носящих неизвестные токи.
Определим количество уравнений, составляемых по первому правилу Кирхгофа, используя формулу:
(4)
где q – количество узлов, входящих в анализируемую цепь. То есть, по первому закону Кирхгофа необходимо составить n 1 = 3 уравнения.
Следовательно, по второму закону Кирхгофа необходимо составить n 2 = 3 уравнения, количество которых вычисляется по формуле:
(5)
Перед составлением системы уравнений необходимо расставить предполагаемые направления текущих токов (рисунок 3).
Рисунок 3 – Графическое представление цепи с
теоретическими направлениями токов
Система уравнений, содержавшая представления первого закона Кирхгофа для узлов 1, 2, 3 и представления второго закона Кирхгофа для контуров I, II, III для анализируемой цепи, в общем виде будет иметь вид:
(6)
Подставив значения сопротивлений и ЭДС в (6), получим:
(7)
Если какое-либо значение тока, в последствие решения, окажется отрицательным, это говорит лишь о том, что он имеет противоположное направление относительно ранее присужденного.
Определение токов методом контурных токов
Метод контурных токов основан на важной топологической особенности электрических цепей, заключающейся в том, что токи всех ветвей цепи связаны между собой (q-1) уравнением баланса токов, и, следовательно, из р токов ветвей только (p-q+l) ток может быть задан независимо. Следовательно, для анализируемой цепи необходимо составить 3 уравнения.
|
|
|
Сокращенная система уравнений электрического равновесия цепи, составленная относительно неизвестных контурных токов, называется системой контурных уравнений цепи и, в нашем случае, имеет вид:
(1)
Zii – собственное сопротивление i-го контура, равная сумме сопротивлений всех ветвей, входящих в этот контур.
Zij – общее, или взаимное, сопротивление i-го и j-го контуров, равное сумме сопротивлений ветвей, общих для этих контуров. Общее сопротивление Zij, берется со знаком плюс, если контурные токи рассматриваемых контуров протекают через общие для этих контуров ветви в одинаковом направлении; если контурные токи в общих ветвях имеют противоположные направления, то общее сопротивление берут со знаком минус. Если контуры цепи не имеют общих ветвей, то их общее сопротивление равно нулю.
Eii – алгебраическая сумма ЭДС всех идеализированных источников напряжения, входящих в i-ый контур. Если направление ЭДС какого-либо источника, входящего в данный контур, совпадает с направлением контурного тока этого контура, то соответствующая ЭДС входит в сумму с положительным знаком, в противном случае — с отрицательным.
Проведем расчеты собственных и взаимных сопротивлений и алгебраических сумм ЭДС контуров анализируемой цепи, требуемые для составления сокращенной системы уравнений электрического равновесия цепи относительно контурных токов:
Таким образом, подставив в систему (1) ранее рассчитанные величины, получим систему уравнений следующего вида:
(2)
Методом Крамера рассчитаем значения контурных токов:
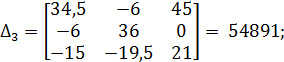
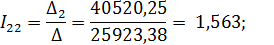
Рассчитаем значения токов всех ветвей анализируемой цепи.
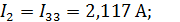
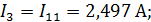
Значение всех токов положительны, это указывает на то, что истинные направления течений токов совпадают с ранее присужденным.
Следовательно, рассматриваемая цепь будет иметь вид (Рисунок 4):
Рисунок 4 – Графическое представление цепи с
|
|
|
истинными направлениями токов
4 Определение токов
|
|
|
