 |
Тема 3 Дифференциальные уравнения
|
|
|
|
Понятие о дифференциальных уравнениях. Общее и частное решения. Задача Коши. Дифференциальные уравнения первого порядка (неполные, с разделяющимися переменными, однородные и линейные). Уравнения, допускающие понижения порядка. Линейные уравнения n-го порядка с постоянными коэффициентами.
Студентам необходимо усвоить определение дифференциального уравнения – как уравнения, которое связывает искомую функцию одной или нескольких переменных и производные различных порядков данной функции.
Дифференциальные уравнения от одной переменной называется обыкновенными дифференциальными уравнениями, дифференциальные уравнения от нескольких переменных – дифференциальные уравнения в частных производных.
Порядок дифференциального уравнения равен порядку старшей степени производной xy¢¢¢-xy¢+5=0 – уравнение третьего порядка.
Нужно помнить, что задача интегрирования дифференциального уравнения – это задача нахождения искомого решения, а график решения называется интегральной кривой.
Общее решение обыкновенного дифференциального уравнения n-го порядка – это функция от переменных х и n произвольных независимых постоянных С1, С2, С0…,Сn.
Частное решение дифференциального уравнения – это решение, полученное из общего при некоторых значениях постоянных.
Для ряда типов дифференциальных уравнений нужно знать студенту основные понятия, нужно уметь решать однородные дифференциальные уравнения, линейные дифференциальные уравнения, неполные дифференциальные уравнения и дифференциальные уравнения с разделяющимися переменными.
Таблица соотношения начальной буквы фамилии студента и варианта контрольных заданий
|
|
|
| Начальная буква фамилии | Вариант задания |
| А, Е, Л | Первый |
| Р, Х, Э | Второй |
| Б, Ж, М | Третий |
| С, Ц, Ю | Четвертый |
| В, З, Н | Пятый |
| Т, Ч | Шестой |
| Г, И, О | Седьмой |
| П, У, Ш | Восьмой |
| Д, Щ, | Девятый |
| Ф, К, Я | Десятый |
ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
ВАРИАНТ №1
Задание №1 Вычислить пределы:
а)  ; б)
; б)  ; в)
; в) 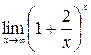
Задание №2 Найти производные функций:а) 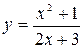 ; б)
; б) 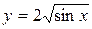 .
.
Задание №3 Исследовать функцию и построить график: у = 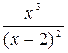 .
.
Задание №4 Найти экстремумы функций двух переменных
z = 2x3 + 6xy2 – 30x – 24y.
Задание № 5. Найти неопределенные интегралы:

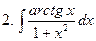

Задание № 6. Найти определенные интегралы:
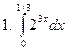
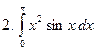
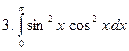
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
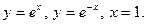
Задание № 8. Решить дифференциальное уравнение первого порядка:
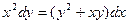
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
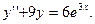
ВАРИАНТ №2
Задание №1 Вычислить пределы: а)  ; б)
; б) 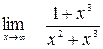 ;
;
в) 
Задание №2 Найти производные функций: а)  ; б)
; б) 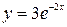 .
.
Задание№3 Исследовать функцию и построить график: 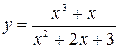 .
.
Задание №4 Найти экстремумы функций двух переменных
z = x3 – y3.
Задание № 5. Найти неопределенные интегралы:
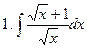

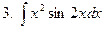
Задание № 6. Найти определенные интегралы:



Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:

Задание № 8. Решить дифференциальное уравнение первого порядка:

Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:

ВАРИАНТ №3
Задание №1 Вычислить пределы: а) 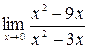 ; б)
; б) 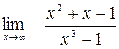 ;
;
в) 
Задание №2 Найти производные функций: а) 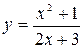 ; б)
; б) 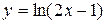 .
.
Задание№3 Исследовать функцию и построить график: 
Задание №4 Найти экстремумы функций двух переменных
z = 6x2у + 2у3 – 24х – 30у.
Задание № 5. Найти неопределенные интегралы:



Задание № 6. Найти определенные интегралы:



Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
|
|
|
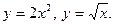
Задание № 8. Решить дифференциальное уравнение первого порядка:

Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
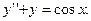
ВАРИАНТ №4
Задание №1 Вычислить пределы: а)  ; б)
; б) 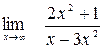 ;
;
в) 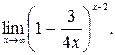
Задание №2 Найти производные функций: а)  ; б)
; б) 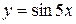
Задание№3 Исследовать функцию и построить график: 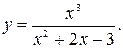
Задание №4 Найти экстремумы функций двух переменных
z = x3 – 8у3 – 6ху + 1.
Задание № 5. Найти неопределенные интегралы:



Задание № 6. Найти определенные интегралы:
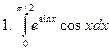
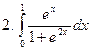
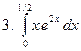
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
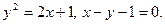
Задание № 8. Решить дифференциальное уравнение первого порядка:

Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
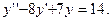
ВАРИАНТ №5
Задание №1 Вычислить пределы: а)  ; б)
; б)  ;
;
в) 
Задание №2 Найти производные функций: а)  ; б)
; б) 
Задание№3 Исследовать и построить график: 
Задание №4 Найти экстремумы функций двух переменных
z = x3 – ху2 + 3х2 + у2 – 1.
Задание № 5. Найти неопределенные интегралы:
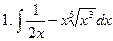
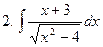

Задание № 6. Найти определенные интегралы:
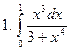

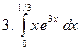
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
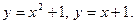
Задание № 8. Решить дифференциальное уравнение первого порядка:
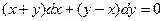
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:

ВАРИАНТ №6
Задание №1 Вычислить пределы: а)  ; б)
; б) 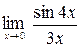 ;
;
в) 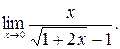
Задание №2 Найти производные функций:а)  ; б)
; б)  .
.
Задание№3 Исследовать функцию и построить график: 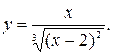
Задание №4 Найти экстремумы функций двух переменных
z = x2у –  у3 + 2х2 + 3у2 – 1.
у3 + 2х2 + 3у2 – 1.
Задание № 5. Найти неопределенные интегралы:

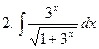

Задание № 6. Найти определенные интегралы:
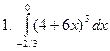


Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:

Задание № 8. Решить дифференциальное уравнение первого порядка:

Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
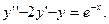
ВАРИАНТ №7
Задание №1 Вычислить пределы: а) 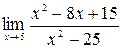 ; б)
; б) 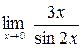 ;
;
в) 
Задание №2 Найти производные функций: а)  ; б)
; б) 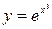 .
.
Задание №3 Исследовать функцию и построить график: 
|
|
|
Задание №4 Найти экстремумы функций двух переменных
z = x3 + 6ху + 3у2 – 18х – 18у.
Задание № 5. Найти неопределенные интегралы:

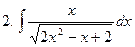

Задание № 6. Найти определенные интегралы:
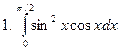
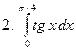

Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:

Задание № 8. Решить дифференциальное уравнение первого порядка:
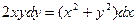
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:

ВАРИАНТ №8
Задание №1 Вычислить пределы: а)  ; б)
; б) 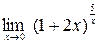 ;
;
в) 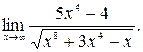
Задание №2 Найти производные функций: а)  ;
;
б)  .
.
Задание№3 Исследовать функцию и построить график: 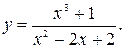
Задание №4 Найти экстремумы функций двух переменных
z = x2у – у3 – х2 – 3у2 +3.
Задание № 5. Найти неопределенные интегралы:
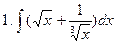
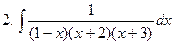

Задание № 6. Найти определенные интегралы:



Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
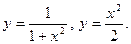
Задание № 8. Решить дифференциальное уравнение первого порядка:

Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:
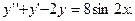
ВАРИАНТ №9
Задание №1 Вычислить пределы: а) 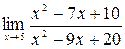 ; б)
; б) 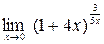 ;
;
в) 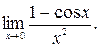
Задание №2 Найти производные функций: а)  ;
;
б)  .
.
Задание№3 Исследовать функцию и построить график: 
Задание №4 Найти экстремумы функций двух переменных
z = 3x2 – 6ху – у3 – 12х + 12у.
Задание № 5. Найти неопределенные интегралы:
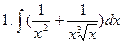
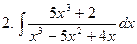

Задание №6. Найти определенные интегралы:


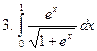
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
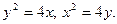
Задание № 8. Решить дифференциальное уравнение первого порядка:
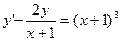
Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:

ВАРИАНТ №10
Задание №1 Вычислить пределы: а)  ; б)
; б)  ;
;
в) 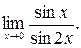
Задание №2 Найти производные функций: а)  ; б)
; б) 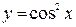 .
.
Задание№3 Исследовать функцию и построить график:  .
.
Задание №4 Найти экстремумы функций двух переменных
z = 2x3 – ху2 + 5х2 + у2.
Задание № 5. Найти неопределенные интегралы:


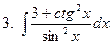
Задание № 6. Найти определенные интегралы:


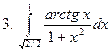
Задание № 7. Выполнить чертеж и решить задачу: Вычислить площадь фигуры, ограниченной линиями:
|
|
|

Задание № 8. Решить дифференциальное уравнение первого порядка:

Задание № 9. Решить линейное дифференциальное уравнение с постоянными коэффициентами:

РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ
Основная литература
1. Балдин, К. В. Математика [Электронный ресурс]: учебное пособие / К. В. Балдин, В. Н. Башлыков, А. В. Рукосуев. - М.: Юнити-Дана, 2012. - 543 с. - 5-238-00980-1. Режим доступа: http://www.biblioclub.ru/index.php?page=book&id=114423 (дата обращения 05.12.2013).
2. Высшая математика для экономистов: практикум: учеб. пособие для студ. вузов / ред. Н. Ш. Кремер. - 2-е изд., перераб. и доп. - М.: ЮНИТИ, 2007. - 478 с. - (Золотой фонд российских учебников)
3. Высшая математика для экономистов: учебник для студ. вузов / Ред. Н. Ш. Кремер. - 3-е изд. - М.: ЮНИТИ, 2010. - 479 с. - (Золотой фонд российских учебников).
4. Высшая математика для экономистов: учебник для студ. вузов / ред. Н. Ш. Кремер. - 3-е изд. - М.: ЮНИТИ, 2006. - 479 с. - (Золотой фонд российских учебников).
5. Высшая математика для экономистов: учебник для студ. вузов / ред. Н. Ш. Кремер. - 3-е изд. - М.: ЮНИТИ, 2007. - 479 с. - (Золотой фонд российских учебников)
6. Высшая математика для экономистов: учебник для студ. вузов / ред. Н. Ш. Кремер. - 3-е изд. - М.: ЮНИТИ, 2008. - 479 с. - (Золотой фонд российских учебников).
7. Высшая математика для экономистов. Учебник и практикум. Ч.1: учебник / Ред. Н. Ш. Кремер. - М.: Высш. образование, 2005. - 486 с. - (Основы наук)
8. Коробейникова И.Ю. Математика. Математическая статистика: учеб. пособие. Ч. 6 / И. Ю. Коробейникова, Г. А. Трубецкая; Южно-Уральский институт управления и экономики. - Челябинск: Полиграф-Мастер, 2010. - 80 с.
9. Кремер Н.Ш. Высшая математика для экономистов: практикум: учеб. пособие для студ. вузов, обуч. по экономическим спец. / Н. Ш. Кремер. - 2-е изд., перераб. и доп. - М.: ЮНИТИ, 2010. - 478 с. - (Золотой фонд российских учебников)
10. Кремер Н.Ш. Высшая математика для экономических специальностей: учебник и практикум: учебник для студ. вузов, обуч. по экон. спец. / ред. Н. Ш. Кремер. - 3-е изд., перераб. и доп. - М.: Юрайт, 2011. - 909 с. - (Основы наук).
11. Кузнецов, Б. Т. Математика [Электронный ресурс]: учебник / Б. Т. Кузнецов. - М.: Юнити-Дана, 2012. - 720 с. - 5-238-00754-Х. Режим доступа: http://www.biblioclub.ru/index.php?page=book&id=114717 (дата обращения 05.12.2013).
12. Математика для юридических специальностей: учеб. пособие для студ. вузов / ред. С. Я. Казанцев. - М.: Академия, 2011. - 217 с. - (Университетский учебник. Высшая математика и ее приложения к юриспруденции).
13. Практикум по высшей математике для экономистов: учеб. пособие для вузов / Ред. Н. Ш. Кремер. - М.: ЮНИТИ, 2005. - 423 с.
14. Уткин, В. Б. Математика и информатика [Электронный ресурс]: учебное пособие / В. Б. Уткин, К. В. Балдин, А. В. Рокосуев. - М.: Дашков и Ко, 2011. - 470 с. - 978-5-394-01337-9. Режим доступа: http://biblioclub.ru/index.php?page=book&id=116015 (дата обращения 21.04.2014).
|
|
|
Дополнительная литература
1. Высшая математика в упражнениях и задачах: учеб. пособие для вузов. В 2 ч.: Ч. 2 / П. Е. Данко [и др.]. - 7-е изд., испр. - М.: ОНИКС, 2008. - 448 с.
2. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1 / П.Е.Данко [и др.]. - 7-е изд., испр. - М.: ОНИКС; М.: Мир и Образование, 2008. - 368 с.
3. Гмурман, В.Е. Теория вероятностей и математическая статистика: учеб. пособие для студ. вузов / В. Е. Гмурман. - 11-е изд., стер. - М.: Высш. шк., 2005. - 479 с.: ил.
4. Данко, П.Е. Высшая математика в упражнениях и задачах: учеб. пособие для вузов. В 2 ч. Ч. 2 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 6-е изд. - М.: ОНИКС, 2005. - 416 с
5. Демидович, Б.П. Краткий курс высшей математики: учеб. пособие для вузов / Б. П. Демидович, В. А. Кудрявцев. - М.: АСТ-Астрель, 2004. - 655 с. Ермаков, В.И. Сборник задач по высшей математике для экономистов / В.И.Ермаков – М.: ИНФРА, 2002
6. Исследование операций в экономике: учеб. пособие для студ. вузов / ред. Н. Ш. Кремер. - М.: ЮНИТИ, 2004. - 407 с.
7. Математика: энциклопедия / ред. Ю. В. Прохоров. - Репринт. изд. "Математического энциклопедического словаря" 1988 г. - М.: Большая рос. энц., 2003. - 847 с.: ил. - (Золотой фонд)
8. Математика. Новейший справочник школьника / Сост. Г. М. Якушева. - М.: Эксмо, 2005. - 479 с.
9. Математика: энцикл. / Ред. Ю.В. Прохоров. - Репринт. изд. - М.: Большая рос. энц., 2003. - 846 с.
Приложение 1
Таблица производных и интегралов

Приложение 2
Список вопросов
Тема 1. Неопределенный интеграл
1. Неопределенный интеграл и его свойства.
2. Интегрирование методом подстановки.
3. Интегрирование по частям.
4. Интегрирование рациональных функций.
5. Интегрирование тригонометрических функций.
Тема 2. Определенный интеграл
1. Определение определенного интеграла и его свойства.
2. Замена переменной в определенном интеграле.
3. Интегрирование по частям в определенном интеграле.
4. Приложение определенного интеграла.
5. Несобственный интеграл. Сходимость несобственного интеграла.
Тема 3. Дифференциальные уравнения
1. Определение дифференциального уравнения. Общее и частное решения.
2. Дифференциальные уравнения с разделяющимися переменными.
3. Однородные дифференциальные уравнения первого порядка.
4. Линейные дифференциальные уравнения первого порядка.
5. Дифференциальные уравнения, допускающие понижения порядка.
6. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами.
Тема 4. Ряды
1. Понятие ряда и его сходимости. Свойства сходящихся рядов.
2. Признаки сходимости положительных рядов.
3. Знакопеременные ряды. Абсолютная и условная сходимость.
4. Функциональные ряды.
5. Степенные ряды. Область сходимости степенного ряда.
6. Ряды Тейлора и Маклорена.
|
|
|


