 |
Задание для самостоятельного решения
|
|
|
|
Лабораторная работа № 5
ПРОГРАММИРОВАНИЕ ИТЕРАЦИОННЫХ ЦИКЛОВ И ВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕССОВ С УСЛОЖНЕННОЙ СТРУКТУРОЙ
Цель и порядок работы
Цель работы – познакомиться со структурным подходом разработки алгоритмов сложных вычислительных процессов, получить практические навыки программирования подобного рода задач.
Порядок выполнения работы:
· ознакомиться с описанием лабораторной работы;
· получить задание у преподавателя по вариантам;
· разработать схему алгоритма решения задачи;
· написать программу, соответствующую схеме алгоритма;
· ввести программу, отладить и выполнить ее на ЭВМ;
· оформить отчет.
·
Общие сведения
В данной лабораторной работе приводится ряд подходов с подробными рассуждениями к решению некоторых задач различных типов.
2.1 Итерационные циклы
Итерационным циклом называется такой, число повторений которого заранее неизвестно или его сложно рассчитать, а в процессе повторения тела цикла образуется последовательность значений y1, y2,…, yn,…, сходящаяся к некоторому пределу а, т. е.
Lim yn = a.
n ® ¥
Каждое новое значение yn в такой последовательности определяется с учетом предыдущего yn-1 и является по сравнению с ним более точным приближением к искомому результату. Итерационный цикл заканчивает свою работу в том случае, если для некоторого значения n выполняется условие:
| yn - yn-1 |£ e,
где e - допустимая погрешность вычисления результата.
В такой ситуации за результат принимают последнее значение y, т.е. считают, что yn с заданной точностью представляет значение а.
Задача вычисления суммы бесконечного ряда может служить прекрасной иллюстрацией к пониманию итерационного циклического процесса. Естественно, вычислять сумму бесконечного ряда имеет смысл в том случае, когда бесконечный ряд является сходящимся. Известно, что ряд сходится, если его общий член zn при беспредельном возрастании n стремится к нулю, т. е.
|
|
|
Lim zn = 0; Lim (sn – sn-1) = 0.
n ® ¥ n ® ¥
А сумма
sn = z0 + z1 + …+zn
его первых (n + 1) слагаемых при этом стремится к некоторому пределу S, который и называется суммой ряда, т. е.
Lim sn = S; Lim S zn = S.
n ® ¥ n ® ¥
Алгоритм, реализующий подсчет суммы ряда, должен вырабатывать последовательность s1, s2, …, sn, … при следующем условии окончания суммирования:
| zn |£ e.
Пример 1. Вычислить значение функции cos x, используя разложение косинуса в ряд с заданной погрешностью e:
Cos x = 1 -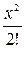 
+ 
- 
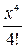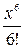+ …+(-1)n 
+...
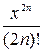При построении алгоритма данной задачи необходимо:
- определить значение очередного слагаемого z ;
- осуществлять накопление суммы по итерационной формуле:
s = s + z.
Для определения значения очередного слагаемого z в данном примере целесообразно использовать не прямое его вычисление по общей формуле, а рекуррентное соотношение, которое позволяет существенно сократить количество операций при вычислении его значения:
z = z * fn.
Определим сомножитель f n:
fn =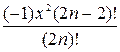 
=. 
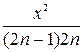
Для работы алгоритма (рис.1) весьма важно определить исходную информацию для работы цикла. Подставив в данную формулу n = 0,получим начальное значение z =1.
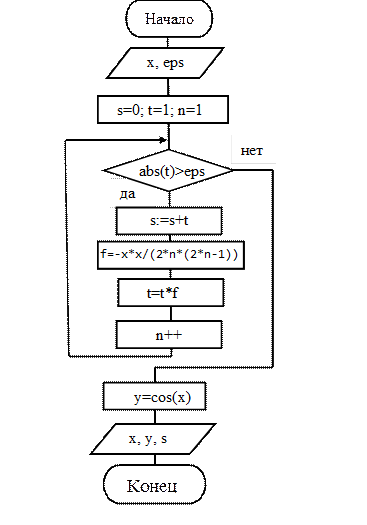
Рисунок 1 – Схема алгоритма к примеру 1
Все вышесказанное реализовано в программе (лист. 1), соответствующей схеме данного алгоритма.
Листинг 1
using System;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
double x, eps,s,t,y,f;
Console.Write("Enter x ");
x = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter eps ");
eps = Convert.ToDouble(Console.ReadLine());
s=0;
t=1;
int n=1;
while (Math.Abs(t) > eps)
{ //Начало цикла
s= s + t;
f= -x*x / (2*n*(2*n-1));
t= t*f;
n++;
} //Конец цикла
y= Math.Cos (x);
Console.WriteLine("х=" + x + " у=" + y+ " s="+s);
}
}
}
Для организации цикла по накоплению суммы используется оператор цикла с предусловием, в котором условие | z | > e является условием продолжения цикла.
|
|
|
Вторым характерным примером использования итерационных циклов является задача решения алгебраических и нелинейных (трансцендентных) уравнений.
Нахождение корней уравнений вида
f (x)= 0
осуществляется в два этапа.
Первый этап – этап локализации корня – определяется отрезок [a,b], в пределах которого находится один и только один корень уравнения. Часто локализация корня осуществляется построением «грубого» графика функции f (x).
Второй этап – этап уточнения корня – ведется поиск корня с заданной степенью точности с помощью некоторого итерационного алгоритма.
Наиболее простым методом уточнения корня является метод итераций, заключающийся в следующем. Исходное уравнение f (x)= 0, где f (x) - непрерывная функция на отрезке [a, b], заменяют эквивалентным уравнением вида:
x = j (x)
и, зная начальное приближение корня x0 Î [a, b], каждое следующее приближение находят по формуле:
xn = j (xn-1).
Вычисления повторяют до тех пор, пока не выполнится условие | f(xn)| £ e, где e - заданная погрешность вычислений. Отметим, что иногда используют другой способ контроля сходимости, состоящей в сравнении xn и xn-1. Процесс сходится, если на всем отрезке [a, b] |j¢(x)|< 1, где j¢(x) есть производная функции j (x).
Пример 2. Определить корень уравнения x – tg(x)= 0 с погрешностью e = 10-3 при начальном значении корня x0 = 4,5.
Преобразуем исходное уравнение следующим образом:
x = tg x,
тогда f(x)= x – tg x; j(x) = tg x.
Для определения x0 удобно использовать следующие графические построения. Построить графики функций y1= x; y2= j(x)= tg x. Точки пересечения этих графиков и будут корнями исходного уравнения f(x)= 0. На графике выделить приближенные отрезки [a, b] локализации каждого корня. В качестве x0 можно взять любую точку отрезка.
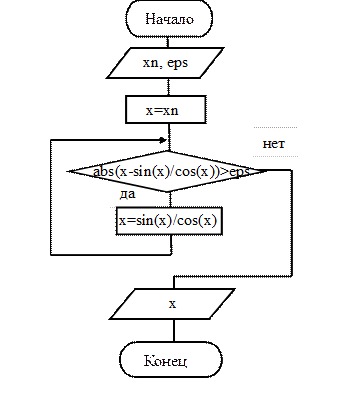
Рисунок 2 – Схема алгоритма к примеру 2
Программа уточнения корня по методу итераций представлена в листинге 2.
Листинг 2
using System;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
double x, xn, eps;
Console.Write("Enter xn ");
xn = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter eps ");
eps = Convert.ToDouble(Console.ReadLine());
x=xn;
while (Math.Abs (x-Math.Sin(x)/Math.Cos(x))>eps)
x=Math.Sin(x)/Math.Cos(x);
Console.WriteLine("x=" + x);
|
|
|
}
}
}
В данной программе на печать в качестве результата выводится последнее значение x, которое удовлетворяет заданному значению Eps.
Для практического контроля сходимости итерационного процесса xn=j(xn-1) можно осуществлять печать промежуточных значений x, последнее из которых и будет корнем уравнения при заданной погрешности.
Вложенные циклы
Если телом цикла является циклическая структура, то такие циклы называют вложенными или сложными. Цикл, содержащий в себе другой цикл, называют внешним. Цикл, содержащийся в теле другого цикла, называют внутренним.
Внутренний и внешний циклы могут быть любыми из трех рассмотренных видов: циклами с параметром, циклами с предусловием, циклами с постусловием. При построении вложенных циклов необходимо соблюдать следующее дополнительное условие: все операторы внутреннего цикла должны полностью лежать в теле внешнего цикла, циклы ни в коем случае не могут пересекаться.
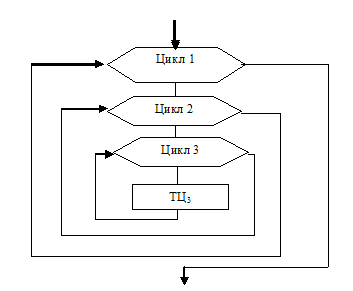
Сложные циклы условно разбивают на уровни вложенности. Ниже представлена структура вложенных циклов с параметром, для которой: внешний цикл 1 имеет уровень 0, внутренний цикл 2 – уровень 1, внутренний цикл 3 – уровень 2.
Возможная глубина вложенности циклов (количество уровней) ограничивается объемом имеющейся памяти ЭВМ. Заметим, что цикл 2 является внешним по отношению к циклу 3 и внутренним по отношению к циклу 1. Параметры циклов разных уровней изменяются не одновременно. Вначале все свои значения изменит параметр самого внутреннего цикла при фиксированных значениях параметров циклов с меньшим уровнем - это цикл 3. Затем меняется на один шаг значение параметра следующего уровня (цикла 2) и снова полностью выполняется внутренний цикл и т. д. до тех пор, пока параметры циклов всех уровней не примут все требуемые значения. При этом, если в сложном цикле с глубиной вложенности k число повторений циклов на каждом уровне равно N0, N1, …, Nk соответственно, то общее количество повторений тела самого внутреннего цикла равно:
N= N0 × N1 × … × Nk .
 |
|
|
|
Рисунок 3 – Схема алгоритма с вложенными циклами
На рис. 3 изображен цикл с параметром. Но все изложенное относится и к тем случаям, когда для организации циклов используются другие виды циклических структур: цикл с предусловием или цикл с постусловием.
Рассмотрим конкретную задачу, требующую для своего решения организации вложенных циклов. Такой задачей является задача табулирования функции нескольких переменных.
Пример 3. Построить алгоритм и написать программу вычисления значений функции z=cos x + y, где x = xn (hx) xk и y = yn (hy) yk. Аргументы функции x, y – действительные числа.
Для определения значений функции z для всех различных пар (x, y) необходимо процесс вычислений организовать следующим образом. Вначале при фиксированном значении одного из аргументов, например при x=x0, вычислить значения z для всех заданных y: yn, yn + hy , …, yn . Затем, изменив значение х на x + hx , вновь перейти к полному циклу изменения переменной y. Данные действияповторить для всех заданных x: xn, xn + hx, …, xn. При реализации данного алгоритма требуется структура вложенных циклов: внешнего цикла – для изменения значений переменной х и внутреннего цикла – для изменения значений переменной у. Причем в данной задаче внешний и внутренний циклы можно поменять местами, при этом изменится только очередность изменения аргументов при вычислении функции. В качестве внешнего и внутреннего циклов можно использовать циклы с параметром, циклы с предусловием или с постусловием.
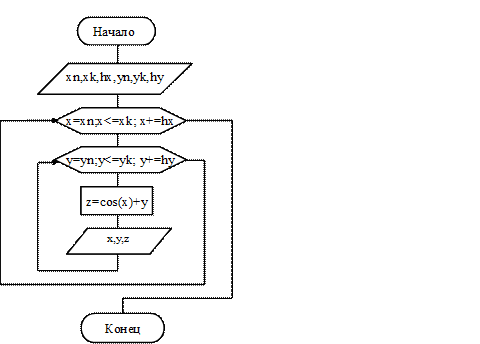
Рисунок 4 – Схема алгоритма к примеру 3
Алгоритм решения поставленной задачи, выполненный с применением цикла с параметром, представлен на рис. 4. Программа, соответствующая этому алгоритму, представлена в листинге 3.
Листинг 3
using System;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
double xn, xk, hx, yn, yk, hy, z;
Console.Write("Enter xn ");
xn = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter xk ");
xk = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter hx ");
hx = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter yn ");
yn = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter yk ");
yk = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter hy ");
hy = Convert.ToDouble(Console.ReadLine());
for (double x = xn; x <= xk; x += hx) // Внешний цикл
{
for (double y = yn; y <= yk; y += hy) // Внутрений цикл
{
z = Math.Cos(x) + y;
Console.WriteLine("х=" + x + " у=" + y + " z=" + z);
}
}
}
}
}
Пример 4. Вычислить с погрешностью e значения функции y = cos(x), используя разложение cos x в ряд, для значений x = xn (hx) xk.
Вычислить значение функции cos x можно путем разложения его в следующий ряд:
Cos x = 1 - 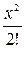+ 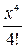- 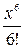+ …+(-1)n +...
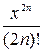Рисунок 5 – Схема алгоритма к примеру 4
Задача вычисления y = cos x для фиксированного значения х была рассмотрена в примере 1. В данном случае сумму ряда S необходимо вычислять для каждого значения х из диапазона [ xn, xk ]. Следовательно, необходимо использовать структуру вложенных циклов. Как показано на схеме алгоритма (рис. 5), внешний цикл – цикл для изменения значений переменной х (цикл с предусловием). Внутренний цикл – цикл для вычисления суммы ряда при фиксированном значении х с погрешностью вычислений e (также цикл с предусловием).
|
|
|
Все вышесказанное реализовано в программе, соответствующей схеме данного алгоритма.
В данном случае сумму ряда S необходимо вычислять для каждого значения х из диапазона [ xn, xk ]. Следовательно, необходимо использовать структуру вложенных циклов. Как показано на схеме алгоритма, внешний цикл – цикл для изменения значений переменной х (цикл с предусловием). Внутренний цикл – цикл для вычисления суммы ряда при фиксированном значении х с погрешностью вычислений e (также цикл с предусловием).
Правильность работы программы оценивается путем сравнения значения s с его вычисляемым по формуле y=cos(x) значением.
Соответствующая программа представлена в листинге 4.
Листинг 4
using System;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
double xn, xk, hx, eps,s,t,y,f;
Console.Write("Enter xn ");
xn = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter xk ");
xk = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter hx ");
hx = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter eps ");
eps = Convert.ToDouble(Console.ReadLine());
double x= xn;
while (x<=xk)
{ //Внешний цикл
s=0;
t=1;
int n=1;
while (Math.Abs(t) > eps)
{ //Внутренний цикл
s= s + t;
f= -x*x / (2*n*(2*n-1));
t= t*f;
n++;
} //Конец внутреннего цикла
y= Math.Cos (x);
Console.WriteLine("х=" + x + " у=" + y+ " s="+s);
x= x + hx;
} //Конец внешнего цикла
}
}
}
Выше были рассмотрены основные управляющие конструкции языка Паскаль, позволяющие осуществлять программную реализацию различных ветвлений и циклов. Любой алгоритм (программа) представляет собой некоторую комбинацию рассмотренных стандартных структур: линейной, разветвляющейся, циклической.
Пример 5. Составить программу нахождения наибольшего общего делителя (НОД) двух целых чисел M и N.
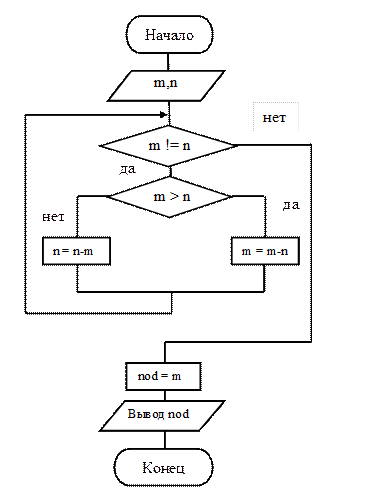
Рисунок 6 – Схема алгоритма к примеру 5
Программа представлена в листинге 5.
Листинг 5
using System;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
int m,n,nod;
Console.Write("Enter m ");
m = Convert.ToInt32(Console.ReadLine());
Console.Write("Enter n ");
n = Convert.ToInt32(Console.ReadLine());
while (m!=n)
{
if (m > n) m= m - n;
else n= n-m;
}
nod= m;
Console.WriteLine("nod=" + nod);
}
}
}
Программа представляет собой сочетание линейной, циклической и разветвляющейся структур. Телом цикла с предусловием является разветвление.
Пример 6.
Составить программу табулирования сложной функции
(a sin x+b cos x)[x]!, если x£ k;
y = f(x) =
если x> k,
действительной переменной x = xn (hx) xk. Для вычисления ln x необходимо воспользоваться формулой:
ln x =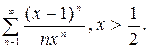 
Вычисления произвести с погрешностью e.
Алгоритм решения поставленной задачи представлен ниже (рис. 7).
Так как вычисление ln x должно производиться при х> 1/2, то при вводе данных необходимо предупредить пользователя о том, чтобы он обратил внимание на значение левой границы интервала изменения х, что и осуществляется в программе.
На первом этапе построим укрупненную схему с выделением операций ввода исходных данных и внешнего цикла по х. В программе этот цикл реализуем с помощью оператора цикла с параметром.
На втором этапе более детально раскроем тело цикла по х без расшифровки вычислений функций факториала и логарифма. Тело цикла представляет собой разветвляющуюся структуру. На последнем этапе раскроем внутренние циклы для вычисления функции ln x и [ x ]!.
Для вычисления [ x ]! используем структуру цикла с параметром, так как [ x ]!=1×2…[ x ].
Вычисление ln x осуществим накоплением суммы членов заданного ряда с требуемой точностью. Везде, где возможно, постараемся использовать рекуррентные формулы.
Рисунок 7 – Схема алгоритма к примеру 6
Программа, соответствующая этому алгоритму, представлена в листинге 6.
Листинг 6
using System;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
double xn, xk, hx, eps, a, b, k, l, t, s, y = 0;
int f;
Console.Write("Enter a ");
a = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter b ");
b = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter k ");
k = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter eps ");
eps = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter xn >1/2 ");
xn = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter xk ");
xk = Convert.ToDouble(Console.ReadLine());
Console.Write("Enter hx ");
hx = Convert.ToDouble(Console.ReadLine());
Console.WriteLine("Исходные данные");
Console.WriteLine("xn=" + xn + " xk=" + xk + " hx=" + hx);
Console.WriteLine("a=" + a + " b=" + b + " k=" + k + " eps=" + eps);
for (double x = xn; x <= xk; x += hx)
{ // Начало внешнего цикла
s = a * Math.Sin(x) + b * Math.Cos(x);
if (x <= k)
{ // Вычисление факториала
f = 1;
for (int n = 1; n <= x; n++)
{
f = f * n;
y = f * s;
}
}
else
{ //Вычисление логарифма
int n = 1; l = 0; t = 1;
do
{
t = t * (x - 1) / x;
l = l + t / n;
n++;
}
while (t >= eps);
y = l / s;
}
Console.WriteLine("x=" + x + " y=" + y);
} //Конец внешнего цикла
}
}
}
Пример 7. Написать программу, запрашивающую ряд целых чисел, среди которых определяется первое отрицательное число, а затем проверяется: является ли абсолютная величина его простым числом.
Программа решения данной задачи представлена в листинге 7.
Листинг 7
using System;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
int n,x;
bool b,t;
Console.WriteLine("ВВедите количество чисел n ");
n = Convert.ToInt32(Console.ReadLine());
b=false;
t=false;
for (int i = 1; i <= n; i++)
{
Console.WriteLine("Введите число х ");
x = Convert.ToInt32(Console.ReadLine());
if (x >= 0) continue;
t = true;
for (int j = 2; j <= Math.Abs(x) - 1; j++)
{
if (Math.Abs(x) % j == 0)
{
b = true;
Console.WriteLine("Число не простое");
break;
}
}
break;
}
if ((b == false) && (t == true))
Console.WriteLine("Число простое");
if (t == false)
Console.WriteLine("Отрицат. чисел нет");
}
}
}
Для решения поставленной задачи использованы вложенные циклы. Внешний цикл обеспечивает ввод заданного количества чисел, внутренний цикл используется для проверки абсолютной величины первого отрицательного числа: является ли она простым числом?
В программе в качестве вспомогательных переменных используются две переменные логического типа: t- принимает значение true, если введено отрицательное число, в противном случае оно сохранит значение false, присвоенное ей в начале работы программы.
Переменная b примет значение true только тогда, когда найдется такое значение j, которое поделит |x| без остатка. Поскольку такое значение j - делитель |x|, то делается вывод о том что, |x| -непростое число. Если b сохранило значение false, то, следовательно, |x| не имеет других делителей, кроме 1 и |x|, а значит оно - простое число.
Для сокращения числа выполняемых операций используются стандартные операторы сontinue и break. Оператор сontinue прерывает выполнение очередной итерации внешнего цикла, если введено неотрицательное число. Оператор break используется здесь дважды. Один раз он прерывает поиск других делителей числа, если один уже найден, осуществляя выход из внутреннего цикла. Сразу же после выхода из внутреннего цикла повторное использование оператора break реализует выход из внешнего цикла, так как по условию задачи нас интересует только первое отрицательное число.
Пример 8. Дано целое число N. Написать программу для получения в порядке убывания всех делителей данного числа. В программе обеспечить пользовательский интерфейс, позволяющий вводить исходные данные и просматривать их, а также неоднократно производить вычисления, не выходя из программы. Для выхода из программы предусмотреть специальную команду.
Ниже приведены схема алгоритма (рис. 8) и программа для решения данной задачи (лист. 8).
В данной программе для реализации поставленной задачи используется цикл с постусловием. С его помощью организуется возможность решения задачи с изменением исходных данных без выхода из программы и повторного ее запуска. Через пользовательское меню возможно осуществить повторный ввод и просмотр данных, получить результаты решения задачи.
Работа пользовательского интерфейса программы обеспечивается с помощью оператора множественного выбора. В данной программе значение селектора b вводится с клавиатуры пользователем. Далее это значение переменной b используется в операторе множественного выбора. Таким образом, пользователь, задавая это значение, определяет, какие операции будет выполнять компьютер. Так, если b =1, то программа выводит на экран предложение ввести исходные данные и считывает их. Если b =2, то на экран выводятся последние значения исходных данных, введенные пользователем. Если b =3, то осуществляется собственно решение задачи, и на экран выводится результат. И если b =4, то осуществляется выход из программы.
Листинг 8
using System;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
int n=0,b;
do
{
Console.WriteLine("- Нажмите 1 и Enter для ввода числа n ");
Console.WriteLine("- Нажмите 2 и Enter для просмотра исходных данных");
Console.WriteLine("- Нажмите 3 и Enter для выполнения программы");
Console.WriteLine("- Нажмите 4 и Enter для выхода из программы");
b = Convert.ToInt32(Console.ReadLine());
switch (b)
{
case 1: Console.WriteLine("ВВедите число n ");
n = Convert.ToInt32(Console.ReadLine()); break;
case 2: Console.WriteLine("n= " +n); break;
case 3: for (int i = n; i>= 1; i--)
{
if (n % i ==0) Console.WriteLine(i);
}
break;
}
}
while (b<4);
}
}
}
Рисунок 8 – Схема алгоритма к примеру 8
Задание для самостоятельного решения
Используя индивидуальные задания к лабораторной работе №4 и подготовленные в процессе ее выполнения три программы решения задачи с различными операторами циклов, построить алгоритм, написать и отладить соответствующую ему программу с двухуровневым меню, организованном с помощью операторов выбора (см. пример 8).
Внешнее меню обеспечивает режимы:
¾ ввод исходных данных;
¾ просмотр результатов;
¾ вход во внутреннее меню;
¾ выход из программы.
Внутреннее меню обеспечивает режимы:
¾ расчет и вывод результатов работы программы с применением оператора цикла с параметром;
¾ расчет и вывод результатов работы программы с применением оператора цикла с предусловием;
¾ расчет и вывод результатов работы программы с применением оператора цикла с постусловием;
¾ выход во внешнее меню.
Содержание отчета
4.1. Титульный лист.
4.2. Краткое теоретическое описание.
4.3. Задание на лабораторную работу, включающее математическую формулировку задачи.
4.4. Результаты выполнения работы, включающие схему алгоритма, тексты программ, результаты вычислений.
|
|
|
