ядер/реакц с выдел-ем энергии. Ядер энергетика.

Вопрос 14.

Явление переноса - Явления состоят в возникновении направленного переноса в газах массы (диффузия), количества энергии (вязкость или внутренне трение) и внутренней энергии (теплопроводность).

Явление теплопроводности (Фурье) - возникает при наличии разности температур в различных слоях газа и в одномерном стационарном случае (T=T(x)) описывается уравнением Фурье: dQ =- K *(dT / dx)* dSdt, где dQ - количество тепла, переносимое за время dt через площадку dS в направлении нормали x к этой площадке в сторону убывания температуры, (dT / dx) - градиент температуры, K - коэффициент теплопроводности. K=(1/3)*ulrc_V. Здесь`u - средняя скорость теплового движения молекул,`l - средняя длина свободного пробега, r - плотность газа, c _V - удельная теплоёмкость газа при постоянном объёме. В общем случае температура T в различных точках тела изменяется с течением времени: T = f (x, y, z, t). x, y, z - координаты точки. t - время.

Явление внутреннего трения / вязкости (Ньютона) - возникновение сил трения между двумя слоями газа или жидкости, перемещающимися параллельно друг другу с различными скоростями. Уравнение Ньютона для вязкости в одномерной задаче (u=u(x)): dF =-h*(d u/ dx)* dS, где dF - сила внутреннего трения, действующая на площадку dS поверхности слоя, (d u/ dx) - градиент скорости движения слоёв в направлении x, перпендикулярном к поверхности слоя, h - коэффициент внутреннего трения. h=(1/3)* ulr.

Явление диффузии (Финк) - процесс установления равновесного распределения концентраций. Диффузия однородного газа в одномерном стационарном случае (r=r(x)) описывается первым законом Фика: dM =- D *(d r/ dx)* dSdt, где dM - масса газа, которая переносится за время dt через элементарную площадку dS в направлении нормали x к рассматриваемой площадке в сторону убыли плотности, (d r/ dx) - градиент плотности, D - коэффициент самодиффузии. D=(1/3)*(u /sqrt(2) n ₀s)=(1/3)*ul, где s - эффективное поперечное сечение соударения молекул, n ₀ число молекул в 1см³.

 

Вопрос 15.
взаимодействие электрических зарядов. Закон Кулона. Понятие напряженности электрического поля. Напряженность поли точечного заряда. Принцип суперпозиции для электрического поля.

Напряжённость электрического поля - его силовая характеристика.

Напряженность электрического поля - вектор E, который численно равен и совпадает по направлению с силой F, действующей со стороны поля на помещённый в рассматриваемую точку единичный положительный заряд q₀: E=F/ q₀.

Точечный заряд - линейный размер тела, на котором этот заряд сосредоточен, намного меньше любых рассматриваемых расстояний.

Поле точечного заряда - Электрический заряд любого тела состоит из целого числа элементарных зарядов, равных 4,8*10^-10. Электрон - отрицательный - масса 9,1*10^-28г. Протон - положительный - масса 1б67*10^-24г. Напряжённость электрического точечного заряда q равна: E =(1/4pe₀)*(q /e r ²)*(r / r), где r - радиус-вектор, проведённый из точечного заряда в исследуемую точку поля; e - относительная диэлектрическая проницаемость среды; e₀ - электрическая постоянная. В скалярной форме: E =(q /e r ²)*(r / r).

Принцип суперпозиции электрических полей - Напряжённость электрического поля системы точечных зарядов равна векторной сумме напряжённостей полей, создаваемых каждым из этих полей в отдельности: E=S_(i=1,n)E_i. *векторная сумма*

Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами.

Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними

Иначе: Два точечных заряда в вакууме действуют друг на друга с силами, которые пропорциональны произведению модулей этих зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды. Эти силы называются электростатическими (кулоновскими).

q1

q2

З.Кулона в векторной записи:

F12= - F21, │F12│= │F21│=F

Fо-это сила вз-вия q в вакууме.

Сила эл/ст вз-явия 2 точечных эл.q находящихся в вакууме прямо пропорционален произ-нию абсолютных значений этих q и обратно проп-лен квадрату рас-ния м/у ними.Сила напр-на вдоль соед.прямой.

В среде вз-вие в ε раз меньше.

ε=F0/F – диэлектрич.проницаемость среды, показ-щая во сколько раз сила вз-вия в вакууме больше чем в среде.

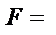
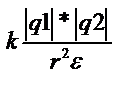
к=1/4πεо,

εо-эл.постоянная =8,85*10(-12) (Кл/Н*м²)

Вопрос 16 Напряжённость электри/п - его силовая характ

Н/эл/п – в-р E, который численно = и совпадает по направлению с F, действующей со стороны поля на помещённый в рассматр-мую т- единичный +й заряд q₀: E=F/ q₀.. Поток ве-ра напряжён-ти электрич/п - сквозь замкнутую пов-сть S: ò_(цирк,S) E _n dS. Это из теор Гаусса для в-ра напряж-ти E в диэлектрике = ò_(цирк,S)(e₀ E _n dS)=S(q _СВОБ)+S(q _СВЯЗ). Где S(q _СВОБ) - это сумма свободных q, охват-ых замкн-ой поверх-ю S, S(q _СВЯЗ) - это сумма связанных q, охваты-ых этой повер-ю.

Теор Остр-Гаусса – поток линий напряж-ти в вакууме сквозь любую замкнутую пов-сть = сумме зq охват-ых этой поверх-ю длинной на Ео.

Расчёт напряжё-ти поля равномерно заряж плоскости (бесконечной) - E =s/(2e₀e), где s - поверхностная плотность зарядов

17/Электрическая ёмкость (электроемкость) - C = q /j (уединённого проводника), где j - потенциал уединённого заряженного проводника, на который не действуют внешние электростатические поля, q - заряд проводника. Уединённого шара: C=4pe₀e R, где R - радиус шара, e - относительная диэлектрическая проницаемость среды, e₀ - электрическая постоянная. Взаимная электроемкость двух проводников - величина, численно равная заряду q, который нужно перенести с одного проводника на другой для того, чтобы изменить разность потенциалов между ними j₁-j₂ на единицу: C= q /(j₁-j₂). Ёмкость плоского конденсатора - это взаимная ёмкость его обкладок. C=e₀e S / d, где S - площадь каждой из пластин или меньшей из них, d - расстояние между пластинами.

Последовательное соединение конденсаторов - C =S_(i=1,n) C _i Параллельное - (1/C)=S_(i=1,n)(1/

Электрическая энергия W _e заряженного проводника - называется его собственной энергией: W _e= C j²/2= q j/2= q ²/2 C, где C - электроёмкость проводника, q - его заряд, j - потенциал проводника. Для конденсаторов в этой формуле: j - разность потенциалов между обкладками, C - ёмкость конденсатора. Энергия заряженного конденсатора - Собственная энергия заряженного тела представляет собой энергию его электрического поля. Для плоского конденсатора его энергия пропорциональна объёму V поля - пространству между обкладками конденсатора: We=(e₀e E ²/2)* V, где E - напряжённость поля, e - относительная диэлектрическая проницаемость среды, e₀ - электрическая постоянная.

 

18. Потенциал поля - его энергетич-я хар-ика. Потенциал в данной т. поля - это скал-я велич-а, численно = Eп W _П единичного «+» зq, помещённого в эту точку: j= W _П/ q.

Разность потенц-в - A, которая совершается F-ми электростатического поля при перемещении точеч электрич з q, = произведению этого заряда на разность потенциалов в начальной 1 и конеч 2 точках пути: A = W _П1- W _П2= q (j₁-j₂) A в электрическом поле - Элементарная A dA, совершаемая силой F, действующей на точ/ электрич зq q ', находящийся в электрич/п с напряжённостью E, равна dA = Fdl cos(F, d l)= q ' E cos(E, d l) dl, где dl – элем-ое перемещ-е q, (E, d l) - угол между направлениями векторов E и d l. Полная A при конечном перемещении заряда q ' из точки n в точку m поля равна: A = q 'ò_(n,m) Edl cos(E, d l).

 

19. Эквипотенц-ая поверх-сть — понятие, применимое к любому потенц-му векторному полю, например, к статическому электрич/п или к ньютоновскому гравитац-му/п. Эквип/пов-сть — это пов-сть, на которой скалярный потенциал данного потенциального поля принимает const значение (пов-сть уровня потенциала). Другое, эквивалентное, опред-ние — пов-сть, в любой своей т ортогональная силовым линиям поля

Напряженность/п Е рассчитывается, как разность потенциалов φ1 - φ2, деленная на расс-ние d между т, в которых берутся эти потенциалы: Е = (φ1 - φ2) / d. И эта формула не выводится, она задаётся. Потому что в науке изначально принято считать напряженностью поля именно то, что я немного выше сказал: разность поненциалов, деленная на расстояние.

Электрич/ток.

 

20. Сила тока - сквозь некоторую поверхность S назыв скал/вел I, равная 1-й производной по t от заряда q, проходящего через эту поверхность: I = dq / dt.

Постоянный ток - когда I и его направление не изменяются с течением t. Для постоянного тока: I = q / t, где q – электр/з, t - время. Сила постоянного тока численно =заряду q, проходящему через поверхность S за единицу времени.

Распределение электр/тока по сечению S харак-тся вектором плотности тока j. Он направлен в сторону в сторону движения «+» зарядов и численно равен: j = dI / dS ', где dS ' - проекция элемента поверхности dS на плоскость, перпендик-ю к j, dI – сила/т сквозь dS и dS '.

Плотность тока (постоянного) - одинакова по всему сечению S проводника. Для постоянного тока I = jS.

З. Ома для произвольного участка цепи - IR ₂₁=(j₁-j₂)+ e ₂₁ или U ₂₁= IR ₂₁. j1 и j2 - значение потенциала электрич/поля в точках 1 и 2. З Ома в диффер-ной форме - U21=ò_(1,2)((E _КУЛ+ E _СТОР) d l)=ò_(1,2)(E d l). E = E _КУЛ+ E _СТОР. E _КУЛ и E _СТОР - напряжённости кулоновских и сторонних сил.

Электри́ч/ сопр-ние — физич/ вел, характер-щая св-ва проводника препятствовать прохождению электрич/т и равная отношению напряжения на концах проводника к с/т, протекающего по нему. Сопр-ние для цепей переменного тока и для переменных электромагн/ полей опис-тся понятиями импеданса и волнового сопр-ия. -ем(резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопр-ния. Сопр-ние (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как R=U/I где R — сопр-ние;- разность электрических потенциалов на концах проводника;

I — с/тока, протекающего между концами проводника под действием разности потенциалов.

Вопрос 21.
Неоднородный участок цепи, понятие электродвижущей силы, действующей на участок цепи. Падение напряжения. ЗаконОмадлязамкнутогоконтура.

 

З.Ома для неоднородного участка цепи

Пусть по неоднор-му уч-ку цепи, где дейст-т стор-е силы поддерж-ся пост-я разность потенц-в и ток пост-й. Полная работа всех сил на неоднор-м уч-ке:

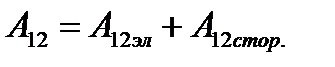
Рез-ом работы явл нагрев-е пров-в:

В итоге получаем:

По определению пост. тока:

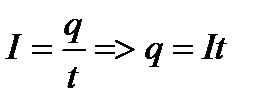
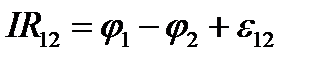
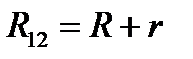
где R – внешн. сопр-е, r – сопр-е источника

а) если уч-к однородный: ε₁₂=0; r=0

б) если рассм-ем замкн-й контур:

 

 

Цепь.амкн-я

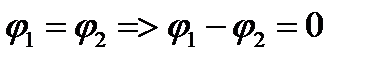
где

Замечание:

запишем з.Ома для неоднород-го уч-ка:

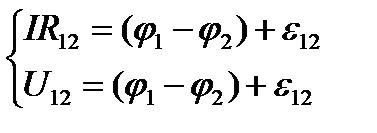
Вывод: падение напряжения на любом уч-ке равно произв-ю тока на сопрот-е этого уч-ка.

 

 

Вопрос 22.
Закон Джоуля-Ленца,. Работа тока. КПД источника тока.

Закон Джоуля-Ленца - для плотности тепловой мощности тока w: w=g E ². w - величина энергии, которая в результате взаимодействия ионов с электронами передаётся ионам кристаллической решётки в единице объёма проводника за единицу времени. g - удельная электропроводимость металла.

Закон Джоуля-Ленца - количество тепла, выделяемого током в проводнике, пропорционально силе тока, времени его прохождения и падению напряжения. Q =0,24 IUt.

Если образующие цепь проводники неподвижны, а электрический ток постоянен, то работа сторонних сил целиком расходуется на нагревание проводников. Энергия W, выделяющаяся в цепи за время t во всём объёме проводника, равна W = IUt. I - сила тока, U - падение напряжения в пров

Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η («эта»). η = Wпол/Wcyм. КПД является безразмерной величиной и часто измеряется в процентах. Математически определение КПД может быть записано в виде:

x 100 %, где А — полезная работа, а Q — затраченная работа.

За время t по цепи протекало количество электричества q. Силы электрического поля, действующего вдоль проводника, перенесли за это время заряд q из точки А в точку Б. Работа электрических сил поля, или, что то же, работа электрического тока, может быть подсчитана по формуле

A=qU

Так как q = It, то окончательно получим

A=UIt

где А — работа, дж; I — ток, а;

t — время, сек;

U —напряжение, в.

Вопрос23.
Расчет разветвленных цепей. Правило Киргофа.

Законы Киргоффа.

.Узел – это точка где сходятся 3 и более проводников.

Закон

Для того, чтобы токи в ветвях не менялись необходимо чтобы потенциал узла ф ост-ся неизменным. Это означает, что кол-во заряда вошедшего в узел = к-ву з-в вышедших из узла.

Алгебраич. сумма токов сходящихся в узле = 0

Токи приход. к узлу положит., выход-е отриц.

Закон

Выделим в разветвл. цепи замкн. Контур

Данный контур можно разбить на 3 неоднородн. уч-ка. Запишем з Ома для кажд. уч-ка. Внутр-ми сопр-ми источника пренебрести.

Уч. АВ:

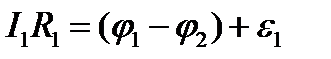
Уч-к ВС:

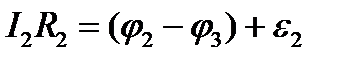
У-к СА: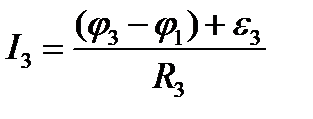

 

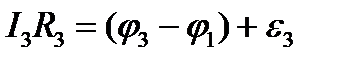
здесь внутр сопр-ми пренебр-ем r₁=r₂=r₃=0

В любом замкн. контуре разв-й цепи алгебраич. сумма произвед-й токов на соотв-е сопр-е = алгебраич-й сумме ЭДС, встреч-ся в замкн-м контуре.

Правило знаков:

1)Если напр. обхода Контура совпадает с напр-ем тока то «+» IR; если не совп-ет то «-«.

2) При переходе в самом источнике от – к + ε со знаком

 

Вопрос 24.
Обратимые и необратимые процессы. Круговой

Обратимые процессы – это идеализация реальных процессов. Термодинамический процесс наз-ся обратимым, если он может происходить как в прямом, так и в обратном направлении и при этом в окружающей среде и самой системе не происходит никаких изменений. Любой процесс неудовлетворяющий этим условиям является необратимым.

Большое значение для применения термодинамики имеют круговые процессы, которые лежат в основе действия всех тепловых машин: холодильников, двигателей, паровых турбин. Тело, совершающее круговой процесс и обменивающееся энергией с др. телами называется рабочим телом. Если тепловая машина преобразовывает теплоту в работу, то это тепловой двигатель, а если посредством работы отнимается теплота у системы, то это холодильник. Круговые процессы изображаются в диаграммах P-V, P-T, V-T в виде замкнутых кривых. Круговой процесс – цикл, потому что за цикл система возвращается в исходное состояние. Если тело получает количество теплоты и совершает работу, то это прямой цикл, а если наоборот, то обратимый.

Чтобы тепловая машина имела возможность совершать работу необходимо наличие холодильника, т.е. тела, которому рабочее тело будет отдавать кол-во теплоты.

а) Q >0 A>0 б) A<0 Q<0

Особое место среди круговых процессов занимает цикл Карно.

Термический КПД – величина, равная отношению работы, совершённой рабочим телом в прямом обратимом цикле, к количеству теплоты, сообщённой в этом процессе нагревателем.

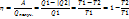
Тепловая машина при данных значениях температуры нагревателя и холодильника не может иметь большего КПД, чем машина, работающая по обратному циклу Карно при тех же значениях температур нагревателя и холодильника.

Цикл Карно является единственным круговым процессом, который, в принципе, можно осуществить обратимым образом.

Адиабатный (∆Q = 0)

25. З Био-Савара-Лапласа - устанавливает величину и направление вектора магн/индукции d B в произвольной точке С магн/п, создаваемого элементом dl проводника с током Id B =m₀*(m/4p)*(I / r ³)*[ d lr ]. В скалярной форме: d B =m*(I / r ³)*(Idl sin(d l, r)/ r ²), где r - радиус-вектор, проведённый из элемента проводника dl в рассматриваемую точку поля, m - относительная магн/проницаемость среды (показывает во сколько раз магнитная индукция/п, созданного током в данной среде, больше чем в вакууме), m₀=4p*10^-7 - магнитная постоянная. В-р dB перпендик-н к плоскости, в которой лежат векторы d l и r, и направлен таким образом, чтобы из его конца кратчайшее вращение вектора d l до совмещения с вектором r казалось происходящим против часовой стрелки. Расчёт напряжённости магн/п прямолинейного проводника с током: Напряж-тью H магн/п называется векторная физ/велич, хар-щая магн/п, созданное движущимися зар-ми и т-ми. Для изотопной среды: H = B /m₀m. Закон БиоСавараЛапласа выражает напряжённость d H, созданную элементом длины d l проводника с током I на расстоянии r от элемента d l: d H =(I /4pr³)[ d lr

 

Вопрос 26.
Индукция магнитного поля в центре кругового тока.

Магнитная индукция - силовая характеристика магнитного поля (вектор B). Определяется из закона Ампера: магнитная индукция B численно равна силе, действующей со стороны магнитного поля на единицу длины проводника, расположенного перпендикулярно к направлению магнитного поля, по которому течёт электрический ток единичной силы.

Вопрос 27.
Циркуляция вектора индукции магнитного поля в вакууме. Магнитное поле бесконечно длинного соленоида.

Теорема о циркуляции – Циркуляция вектора H напряжённости магнитного поля вдоль замкнутого контура L называется интеграл вида: ò_(ЦИРК,L)(H d l)= ò_(ЦИРК,L)(Hdl cos(H, d l)), где L - контур произвольной формы, d l - элемент длины контура в направлении его обхода.

Закон полного тока для токов проводимости: циркуляция вектора напряжённости магнитного поля постоянного электрического поля вдоль замкнутого контура пропорциональна алгебраической сумме токов, охватываемых этим контуром: ò_(ЦИРК,L)(H d l)= ò_(ЦИРК,L)(Hdl cos(H, d l))=S_(k=1,n) I _k, где n - число всех проводников с токами, охватываемых контуром L произвольной формы.

H – напряжённость магнитного поля, физическая величина, характеризующая магнитное поле, созданное движущимися зарядами и точками, и не зависящих от магнитных свойств среды.

B – магнитная индукция, силовая характеристика магнитного поля.

Расчёт магнитного поля тороида (кольцевая катушка, намотанная на сердечник, имеющая форму тора) – магнитное поле тороида целиком локализовано внутри его объёма и равно: B =mm₀*(NI /2p r), H = NI /2p r. Напряжённость поля внутри тороида уменьшится от H _МАКС= NI /2p R ₁ до NI /2p(R ₂+ d), где R ₁ и R ₂ – внешний и внутренний радиусы тора, N и d – число и диаметр витков обмотки, m₀ – магнитная постоянная, m - относительная магнитная проницаемость среды.

Расчёт магнитного поля соленоида (цилиндрическая катушка, состоящая из большого числа витков проволоки, образующих винтовую линию) – магнитное поле соленоида в произвольной точке A соленоида, лежащей на его оси: B=(mm₀/2)* nI *(cosa₂-cosa₁), H= (nI /2)*(cosa₂-cosa₁), где n = N / L – число витков на единицу длины соленоида, a₁ и a₂ - углы, под которыми из точки A видны концы соленоида (a₁>a₂).

Вопрос 28.
Действие магнитного поля на проводник с током-сила Ампера. Взаимодействие бесконечно длинных проводников с током. Единица тока 1А.

Закон Ампера – выражает силу, которая действует на элемент длины проводника с током I, помещённого в магнитное поле (сила Ампера): d F = kI [ d lB ], где dF – сила, dl – вектор элемента длины проводника, проведённый в направлении тока, k – коэффициент пропорциональности, зависящий от выбора единиц измерения для всех входящих в закон величин. При измерении всех величин в единицах одной и той же системы k=1.

Вопрос 29.
Сила Лоренца. Действие частицы по окружности, радиус окружности, период вращения частицы.

Сила Лоренца – действует на электрический заряд, движущийся в магнитном поле: F _Л= q [ vB ], где q – алгебраическая величина движущегося заряда (q >0 для положительного заряда и q <0 для отрицательного заряда), v – скорость заряда, B – магнитная индукция поля, в котором движется заряд. При совместном действии на движущийся заряд электрического и магнитного полей: F _Л= q E + q [ vB ], где E – напряжённость электрического поля.

Движение заряженных частиц в однородном магнитном поле (перпендикулярном к направлению скорости частицы) – частица, под действием силы Лоренца движется по окружности постоянного радиуса r в плоскости, перпендикулярной к вектору B: r =(m /| q |)*(u / B), где m – масса частицы, | q | - абсолютная величина её заряда, u - скорость частицы, B – магнитная индукция.

Движение частицы в однородном магнитном поле.

В зависимости от угла между V и B частица в магнитном поле движется по разны траекториям.

а)α=(V^B)=0⁰

F_л=qVBsin0=0

Согласно I з. Ньютона если на тело не действуют силы то оно движется равномерно и прямолинейно.

б) Частица влетает перпендикулярно полю.

α=(V^B)=90⁰ sin90=1

F_л перпендикулярна V (векторы) вызывает нормальное ускорение частица будет вращатся в поле по окружности по радиусу R.

F_л=qVB

F_л=ma_n=mV²/2

qVB=mV²/R

R=mV/qB

Вращение характеризуется периодом Т.

Е- время одного оборота

Так как сила Лоуренса в данном случае меняет направленискорости а величина её постоянная то вращение равномерное.

T=2πR/V= 2πmV/qBV=2πm/qB

в) 0<α<90

Разложим скорости на составляющие. V=V_ll+V_┴

V_ll- вызывает равномерное движение по полю.

V_┴-Вызывает равномерное вращение в плоскости _┴ полю по окружности радиуса R/

В результате получаем движение по спирали.

h-расстояние пройденное линией вдоль поля со скоростью V_ll за Т.

h=υ││T= υ cosα T

Вопрос 30.
Явление электро магнитной индукции. Закон Фарадея и Ленца. Принцип действия генератора пременного тока. Тока Фуко.

Магнитный поток Ф_m – в магнитной цепи как сила тока в электрической цепи

Электромагнитная индукция – явление, состоящее в том, что в проводящем контуре, находящемся в переменном магнитном поле, возникает ЭДС индукции e_i. Если контур замкнут, ио в нём возникает электрический ток – индукционный ток.

Закон Фарадея – ЭДС электромагнитной индукции e_i в контуре численно равна и противоположна по знаку скорости изменения магнитного потока Ф_m сквозь поверхность, ограниченную этим контуром: =- d Ф_m/ dt.

Правило Ленца – индукционный ток в контуре всегда имеет такое направление, что создаваемый им магнитный поток сквозь поверхность, ограниченную контуром, уменьшает те изменения магнитного потока, которые вызвали появление индукционного тока.

Вихревые токи или токи Фуко́ (в честь Ж. Б. Л. Фуко) — вихревые индукционные токи, возникающие в проводниках при изменении пронизывающего их магнитного потока.

Впервые вихревые токи были обнаружены французским учёным Д.Ф Араго (1786—1853) в 1824 г. в медном диске, расположенном на оси под вращающейся магнитной стрелкой. За счёт вихревых токов диск приходил во вращение. Это явление, названное явлением Араго, было объяснено несколько лет спустя M. Фарадеем с позиций открытого им закона электромагнитной индукции: вращаемое магнитное поле наводит в медном диске токи (вихревые), которые взаимодействуют с магнитной стрелкой. Вихревые токи были подробно исследованы французским физиком Фуко (1819—1868) и названы его именем. Он открыл явление нагревания металлических тел, вращаемых в магнитном поле, вихревыми токами.

Токи Фуко возникают под воздействием переменного электромагнитного поля и по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Они вихревые, то есть замкнуты в кольца. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко достигают очень большой силы. В соответствии с правилом Ленца они выбирают внутри проводника такое направление и путь, чтобы противиться причине, вызывающей их. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это свойство используется для демпфирования подвижных частей гальванометров, сейсмографов и др.

Тепловое действие токов Фуко используется в индукционных печах — в катушку, питаемую высокочастотным генератором большой мощности, помещают проводящее тело, в нем возникают вихревые токи, разогревающие его до плавления.

С помощью токов Фуко осуществляется прогрев металлических частей вакуумных установок для их дегазации.

Во многих случаях токи Фуко могут быть нежелательными. Для борьбы с ними принимаются специальные меры: с целью предотвращения потерь энергии на нагревание сердечников трансформаторов, эти сердечники набирают из тонких пластин, разделённых изолирующими прослойками. Появление ферритов сделало возможным изготовление этих проводников сплошными.

Вопрос 31.
Явление самоиндукции. Полный магнитный поток. Индуктивность контуров. ЭДС самоиндукции. Экстратоки замыкания и размыкания.

Самоиндукция – явление возникновения ЭДС индукции в цепи в результате изменения тока в этой цепи. Магнитное поле тока создаёт магнитный поток Ф_m сквозь поверхность S, ограниченную самим контуром: Ф_m=ò_(S)B_n dS.

Индуктивность L – численно равна магнитному потоку, охватываемому контуром, когда сила тока в контуре равна единице. Ф_m= LI.

Соленоид – цилиндрическая катушка, состоящая из большого числа витков проволоки, образующая винтовую линию.

Расчёт индуктивности соленоида (l – длина, S – площадь поперечного сечения, N – число витков) – L = k *((m₀mN² S)/ l)= k m₀m n ² V, где n = N / l – число витков на единицу длины, V = Sl – объём соленоида, k – коэффициент размагничивания (зависит от отношения длины l соленоида к диаметру d его витков \\ k – таблица\\), m₀ – магнитная постоянная, m - относительная магнитная проницаемость среды.

ЭДС самоиндукции e_C – определяется по закону Фарадея: e_C=- d (Ф_m)/ dt =- d (LI)/ dt

Магнитный поток Ф_m – в магнитной цепи как сила тока в электрической цепи

При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Вопрос 32.
Гармонические колебания, их характеристики. Затухающие колебания

Колебательная система взаимодействует с окружающей средой. На систему действует 2 силы.

1. 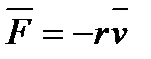(1) сила сопротивления

При незначительных отклонениях от равновесия, величину Fс можно считать пропорциональной скорости системы. 2.Помимо этого, на систему действует квазиупругая сила:

По второму закону Ньютона: ma=F+Fc

ma=-rV – kx-диф.ур-ние затух.кол-ний

mx"= - rx'-kx

mx"+ rx'+ kx=0 x"+(r/m)x'+(k/m)x=0 (2)

Уравнение (2) можно рассматривать, как закон движения системы, совершающий затухающие колебания.

k/m=ω²; r/m=2δ

ω0²- собственная циклическая частота кол-ний.

δ- коэффициент затухания [δ]=[cˉ¹]

x"+2δx'+ωо²х=0 (2') – дифференциальное уравнение второго порядка.

ω0-собственная цикл.частотакол-ний

решением данного ур-ния и будет закон затух.колебония: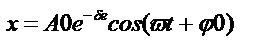

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.

В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.

Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:

Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равени не зависит[1] от амплитуды и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.

 

Вопрос 33.
Волновое движение. Уравнение плоской упругой волны. Длина волны. Фазовая скорость.

Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры[1]».

В связи с этим волновой процесс может иметь самую разную физическую природу: механическую, химическую (реакция Белоусова — Жаботинского, протекающая в автоколебательном режиме каталитического окисления различных восстановителей бромисто-водородной кислотой HBrO3), электромагнитную (электромагнитное излучение), гравитационную (гравитационные волны), спиновую (магнон), плотности вероятности (ток вероятности) и т. д.

Многообразие волновых процессов приводит к тому, что никаких абсолютных общих свойств волн выделить не удаётся[2]. Одним из часто встречающихся признаков волн считается близкодействие, проявляющееся во взаимосвязи возмущений в соседних точках среды или поля, однако в общем случае может отсутствовать и она[2].

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой. По аналогии с возникающими волнами в воде от брошенного в неё камня — расстояние между двумя соседними гребнями волны. Одна из основных харак

Поделиться:

Воспользуйтесь поиском по сайту: