 |
Решение задач на использование свойств натуральных и целых чисел из кимов ЕГЭ
|
|
|
|
Подготовка к ЕГЭ стала самой важной составляющей деятельности учащихся и учителей старшей школы.
В ЕГЭ последние годы очень часто встречаются задания повышенной сложности, требующие определенных знаний и умений. Необходимо не только знать стандартные алгоритмы, но и элементы решения олимпиадных заданий.
Данная тема, раскрывающая использование свойств натуральных и целых чисел, очень актуальна, поскольку она постоянно встречается в заданиях единого государственного экзамена.
Цель работы: обобщить имеющиеся понятия и свойства натуральных и целых чисел, рассмотреть наиболее часто встречающиеся задачи из КИМов ЕГЭ и предложить оптимальный способ их решения.
Задачиисследования:
1. На основе анализа имеющейся литературы по теме исследования систематизировать материал.
2. Привести комплекс заданий, необходимых для закрепления понятий.
Объектом исследования является не только натуральные и целые числа, но и основные школьные темы, в которых они встречаются. Так, к ним относятся делимость, уравнения, прогрессии.
§1. Теоретическая часть
п. 1.1. Числа.
Математика начинается с множества N натуральных чисел, т.е. с чисел 1,2,3,…. Множество N всех натуральных чисел, упорядоченных в строго определенной указанной выше последовательности, называют натуральным рядом чисел или натуральным рядом.
На множестве натуральных чисел, вычитание выполнимо не всегда. Для возможно образования разности любых двух натуральных чисел возникла необходимость расширения множества натуральных чисел. Вводятся число нуль и целые отрицательные числа: -1, -2, -3, …, -n,….
Натуральные числа также называются целыми положительными числами. Целые числа – числа, принадлежащие объединению множества N, множества чисел, противоположных натуральным, и множества, состоящего из одного числа нуль, т.е. целыми называются числа  … и это множество обозначают символом Z.
… и это множество обозначают символом Z.
|
|
|
Рациональными (множество Q) называются числа вида  , где m является целым числом, а n - натуральное число. Эти числа содержат в себе целые числа, и рациональные числа можно понимать как корни уравнения
, где m является целым числом, а n - натуральное число. Эти числа содержат в себе целые числа, и рациональные числа можно понимать как корни уравнения  .
.
Конечные и бесконечные десятичные дроби (множество всех точек числовой оси) образуют множество действительных чисел R. Действительные числа, не являющиеся рациональными, называются иррациональными числами.
Действительные числа, которые не являются корнями многочленов с целыми коэффициентами, называются трансцендентными числами.
п.1.2. Свойства делимости целых чисел.
Пусть n – целое число, m – натуральное число. Говорят, что n делится на m, если существует целое число p такое, что n=mp. Число m называется делителем числа n, p - частным от деления n на m.
Наибольшее натуральное число, являющееся натуральным делителем каждого из натуральных чисел m и n, называют наибольшим общим делителем этих чисел и обозначают НОД(m,n) или (m,n).
Два натуральных числа m и n называют взаимно простыми и пишут (m,n)=1, если единственным общим натуральным делителем этих чисел является число 1.
Свойства делимости суммы (разности) и произведения чисел ( ,
,  ,
, 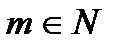 ):
):
1. Если a и b делятся на m, то числа a+b и a-b также делятся на m.
2. Если a и b делятся на m, то при любых целых числах k и l число ak+bl также делится на m.
3. Если a делится на m, а b не делится на m, то числа a+b и a-b также не делятся на m.
4. Если a делится на m, а m делится на  , то число a также делится на k.
, то число a также делится на k.
5. Если a делится на m, а b не делится на m, то число ab делится на m.
6. Если a делится на каждое из чисел m и k, причем (m,k)=1, то a делится на произведение mk.
7. Если a делится на m, то ak делится на mk при любом  .
.
|
|
|
8. Если ab делится на m и b взаимно просто с m, то a делится на m.
Натуральное число p называется простым, если p>1 и p не имеет положительных делителей, отличных от 1 и p. Легко следует, что если p и p1 - простые числа и p делит p1, то p=p1. Кроме того, для любого натурального числа его наименьший отличный от единицы положительный делитель является простым числом.
Натуральное число n>1 называется составным, если n имеет, по крайней мере, один положительный делитель, отличный от 1 и n.
Теорема Евклида: Множество положительных простых чисел бесконечно.
Теорема. Для любого целого числа  в натуральном ряду можно найти k составных чисел, непосредственно следующих друг за другом.
в натуральном ряду можно найти k составных чисел, непосредственно следующих друг за другом.
Теорема. Если произведение нескольких натуральных чисел делится на простое число, то на него делится хотя бы один из сомножителей.
Представление натурального числа n в виде произведения двух натуральных чисел ab называется разложением на множители. Представление числа в виде произведения простых чисел называется разложением на простые множители.
Два разложения на множители называются одинаковыми, если они отличаются только порядком множителей. Например, 42=2  3
3  7 и 42=7
7 и 42=7  2
2  3 считаются одинаковыми.
3 считаются одинаковыми.
Основная теорема арифметики: Для каждого натурального числа n>1 существует единственное разложение на простые множители.
Это значит, что для любого натурального числа два разложения на простые множители могут отличаться только порядком этих множителей.
Каноническим разложением целого числа n>1 называется представление n в виде  , где p1, p2, …, ps – попарно различные простые числа, а k1, k2, …, ks – натуральные числа. Для отрицательных целых чисел n<-1 каноническим разложением считается представление в виде
, где p1, p2, …, ps – попарно различные простые числа, а k1, k2, …, ks – натуральные числа. Для отрицательных целых чисел n<-1 каноническим разложением считается представление в виде  .
.
Количество натуральных делителей числа n, записанного в канонической форме, равно  .
.
Если натуральное число n имеет одно нечетное число натуральных делителей, включая 1 и n, то это число n – полный квадрат.
Пусть  каноническое разложение на простые множители натурального числа n. Тогда число
каноническое разложение на простые множители натурального числа n. Тогда число  , равное сумме всех натуральных делителей числа n, выражается формулой
, равное сумме всех натуральных делителей числа n, выражается формулой  .
.
п.1.3. НОД и НОК. Взаимно простые числа.
Наибольшим общим делителем (НОД) натуральных чисел a1, a2, …, an называется наибольшее натуральное число, на которое делятся данные числа. Наименьшим общим кратным (НОК) – наименьшее натуральное число, делящееся на каждое из этих чисел. Наибольший общий делитель чисел a1, a2, …, an обозначают (a1, a2, …, an), а наименьшее общее кратное – [ a1, a2, …, an ].
|
|
|
НОД (a,b)= НОД(a,a+b), НОД(a,b)=НОД(a,a-b).
Числа a1, a2, …,an называются взаимно простыми, если (a1, a2, …,an)=1 и попарно взаимно простыми, если любые два из них взаимно просты, т.е. (ai,aj)=1 при  .
.
· Если целые числа a и b взаимно просты, то их сумма a+b и произведение ab также являются взаимно простыми числами.
· Если целые числа a и b взаимно простыми, то НОД(a+b, a-b) равен 1 или 2.
· Любые два последовательных натуральных числа взаимно просты.
· Наибольший общий делитель любых двух последовательных четных натуральных чисел равен 2.
· Любые два последовательных нечетных натуральных числа взаимно просты.
· Если целые числа a и b являются взаимно простыми, то НОД(a+b, a2-ab+b2) равен 1 или 3.
· Если натуральные числа m и n взаимно просты, то НОД(m+n,m2+n2) равен 1 или 2.
п.1.4. Свойства остатков при делении целых чисел
Выполнение ряда заданий типа С6 связано с исследованием остатков при делении целых чисел.
Не всякое целое число a делится нацело на данное натуральное число m. Деление числа a на число b с остатком есть отыскание наибольшего натурального числа, которое в произведении с делителем дает число, не превышающее делимого: a=qb+r,  . Искомое число q называется неполным частным. Разность r между делимым и произведением делителя на неполное частное называется остатком. Если остаток равен нулю, то говорят, что a делится на b (без остатка или что число b – делитель числа a).
. Искомое число q называется неполным частным. Разность r между делимым и произведением делителя на неполное частное называется остатком. Если остаток равен нулю, то говорят, что a делится на b (без остатка или что число b – делитель числа a).
Теорема. Для любого целого a и целого b>0 существуют и притом единственные целые q и r такие, что a=qb+r,  .
.
При решении конкретных задач могут потребоваться также таблицы остатков при делении на другие натуральные числа. Приведем некоторые из них.
Остатком при делении целого числа n на 3 могут быть числа 0,1,2. А вот квадраты остатков при делении на 3 дают лишь остатки 0 и 1. Приведем таблицу остатков при делении на 3 чисел n, n2, n3, n4.
|
|
|
| n | n2 | n3 | n4 |
Остатком при делении целого числа n на 4 могут быть числа 0,1,2,3. Приведем таблицу остатков при делении на 4 чисел n, n2, n3, n4:
| n | n2 | n3 | n4 |
Из приведенной таблицы можно сделать ряд выводов, заметить, в частности, что квадраты целых чисел не могут давать остаток 3 при делении на 4.
Остатком при делении целого числа n на 5 могут быть числа 0,1,2,3,4. Приведем таблицу остатков при делении на 5 чисел n, n2, n3, n4:
| n | n2 | n3 | n4 |
Из приведенной части видно, в частности, что число n2+n3 не может давать остатки 3 и 4 при делении на 5.
Таблица остатков при делении на 6 чисел n, n2, n3, n4:
| n | n2 | n3 | n4 |
Таблица остатков при делении на 7 чисел n, n2, n3, n4:
| n | n2 | n3 | n4 |
Таблица остатков при делении на 8 чисел n, n2, n3, n4:
| n | n2 | n3 | n4 |
п.1.5. Четные и нечетные числа
Целое число, делящееся на 2, называется четным, а целое число, не делящееся на 2, называется нечетным.
Два целых числа называются числами одинаковой четности, если оба они четные или нечетные. Два целых числа называются числами разной четности, если одно из них четное, а другое нечетное.
Свойства четных и нечетных чисел:
o Сумма четного и нечетного чисел – число нечетное.
o Сумма любого количества четных чисел – число четное.
o Сумма любого количества нечетных чисел – число четное, если количество слагаемых четно, и нечетное, если количество слагаемых нечетно.
o Произведение нескольких целых чисел четно, если хотя бы один из множителей четен.
o Произведение нескольких целых чисел нечетно, если все их множители нечетны.
o Сумма и разность любых двух целых чисел имеют одинаковую четность.
п.1.6. Десятичная запись натурального числа
Любое натуральное число n можно представить в десятичной системе счисления в виде:  .
.
Например, двузначное число:  , трехзначное число
, трехзначное число  .
.
Признаки делимости натуральных чисел:
o Число n делится на 2 тогда и только тогда, когда  делится на 2.
делится на 2.
o Число n делится на 4 тогда и только тогда, когда  делится на 4.
делится на 4.
o Число n делится на 8 тогда и только тогда, когда  делится на 8.
делится на 8.
|
|
|
o Число n делится на 3 тогда и только тогда, когда сумма всех его цифр делится на 3.
o Число n делится на 9 тогда и только тогда, когда сумма всех его цифр делится на 9.
o Число n делится на 5 тогда и только тогда, когда 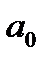 делится на 5.
делится на 5.
o Число n делится на 25 тогда и только тогда, когда  делится на 25.
делится на 25.
o Число n делится на 125 тогда и только тогда, когда 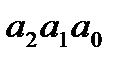 делится на 125.
делится на 125.
o Число делится на 10 тогда и только тогда, когда его последняя цифра 0.
o Число делится на 11 тогда и только тогда, когда делится на 11 сумма  .
.
Некоторые признаки делимости являются следствием вышеприведенных признаков делимости.
Например, число делится на6 тогда и только тогда, когда оно делится на 2 и на 3. Делимость на 12 равносильна делимости на 3 и на 4, делимость на 15 равносильна делимости на 3 и на 5 и т.д.
Общий признак делимости чисел:
Для того чтобы число М делилось на d, необходимо и достаточно, чтобы сумма произведений цифр этого числа на остатки, получаемые от деления на d соответствующих степеней числа 10, делились на d. Действительно, пусть  и
и  ,…,
,…,  ,
, 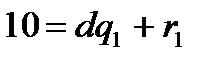 .Тогда М делится на d в том и только том случае, если на d делится сумма
.Тогда М делится на d в том и только том случае, если на d делится сумма  .
.
o При любом целом a разности a2-a делится на 2.
o При любом целом a разности a3-a делится на 3.
o Если p -простое число и число a не делится на p, то ap-1-1 делится на p.
o Число 4 n при делении на 3 дает в остатке 1.
o Число 5 2n при делении на 3 дает в остатке 1, а 5 2n+1 дает в остатке 2.
п.1.7. Уравнения в целых числах
Уравнение вида  , переменные в котором считаются целочисленными, называется уравнением в целых числах, или диофантовым уравнением. Набор целочисленных значений переменных, при подстановке которых в уравнение получается верное равенство, называется решением диофантова уравнения.
, переменные в котором считаются целочисленными, называется уравнением в целых числах, или диофантовым уравнением. Набор целочисленных значений переменных, при подстановке которых в уравнение получается верное равенство, называется решением диофантова уравнения.
Уравнение вида  называется линейным диофантовым уравнением.
называется линейным диофантовым уравнением.
Если пара чисел  является решением такого уравнения, то все его решения можно получить по формулам
является решением такого уравнения, то все его решения можно получить по формулам  ,
,  .
.
Обычно указанную пару решений находят подбором, подставляя вместо одной переменной остатки от деления на коэффициент при другой.
Также существуют такие методы решения уравнений в целых числах: используя неравенства, используя отношения делимости, выделяя целую часть, методом остатков, методом «спуска», методом последовательного уменьшения коэффициентов по модулю, используя конечные и цепные дроби.
Нелинейные уравнения решаются следующими методами: методом вынесения общих множителей за скобку, применением формул сокращенного умножения, способом группировки, разложением квадратного трехчлена, используя параметр.
п.1.8. Прогрессии
Арифметическая прогрессия – последовательность, заданная следующим образом:  , где
, где 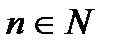 . Число
. Число  называется разностью арифметической прогрессии. Говорят также, что несколько чисел образуют арифметическую прогрессию, если они являются последовательными числами некоторой последовательности, которая является арифметической прогрессией.
называется разностью арифметической прогрессии. Говорят также, что несколько чисел образуют арифметическую прогрессию, если они являются последовательными числами некоторой последовательности, которая является арифметической прогрессией.
Формула n -ого члена арифметической прогрессии  .
.
Геометрическая прогрессия – последовательность, заданная следующим образом:  , где
, где 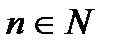 . Число
. Число  ,
,  называется знаменателем геометрической прогрессии.
называется знаменателем геометрической прогрессии.
Формула n -ого члена геометрической прогрессии  . Формула суммы первых n членов геометрической прогрессии
. Формула суммы первых n членов геометрической прогрессии  .
.
Последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому соседних, то есть для любого  ,
,  выполняется равенство
выполняется равенство  .
.
В частности, три числа a, b, с образуют арифметическую прогрессию тогда и только тогда, когда  .
.
Последовательность является геометрической тогда и только тогда, когда модуль каждого ее члена, начиная со второго, равен среднему геометрическому соседних, т.е. для любого  ,
,  выполняется равенство
выполняется равенство  .
.
В частности, три числа a, b, с образуют геометрическую прогрессию тогда и только тогда, когда  .
.
§2. Практическая часть
Пример 1
Найдите натуральные числа m и n, удовлетворяющие соотношению  (
( ,n=1,2,3…).
,n=1,2,3…).
Решение.
При  первое и второе слагаемые в левой части соотношения делятся на 3. Следовательно, в этом случае остаток от деления левой части на 3 определяется числом 23 и равен 2. Но, из таблицы остатков при делении на 3, остаток от деления m2 на 3 не может быть равен 2, поэтому в ответе не могут быть числа
первое и второе слагаемые в левой части соотношения делятся на 3. Следовательно, в этом случае остаток от деления левой части на 3 определяется числом 23 и равен 2. Но, из таблицы остатков при делении на 3, остаток от деления m2 на 3 не может быть равен 2, поэтому в ответе не могут быть числа  . Подставляя в заданное соотношение
. Подставляя в заданное соотношение  и
и 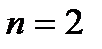 , находим два решения:
, находим два решения:  ,
,  и
и  ,
,  .
.
Ответ:  ,
,  и
и  ,
,  .
.
Пример 2
Найдите натуральные числа k и m, удовлетворяющие соотношению  .
.
Решение.
При 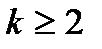 первое слагаемое в левой части соотношения делится на 9. Следовательно, в этом случае остаток от деления левой части на 9 определяется числом 86 и равен 5. Но, из таблицы остатков при делении на 9, остаток от деления m3 на 9 не может быть равен 5, поэтому в ответе не могут быть числа
первое слагаемое в левой части соотношения делится на 9. Следовательно, в этом случае остаток от деления левой части на 9 определяется числом 86 и равен 5. Но, из таблицы остатков при делении на 9, остаток от деления m3 на 9 не может быть равен 5, поэтому в ответе не могут быть числа  . Подставляя в заданное соотношение
. Подставляя в заданное соотношение  , находим решение
, находим решение  ,
,  .
.
Ответ:  ,
,  .
.
Пример 3
Если в натуральном числе первую цифру поменять с последней цифрой, то число увеличится на 75%. Найдите все такие двузначные числа.
Решение.
Пусть первая цифра искомого числа равна a, а вторая цифра равна b, т.е. число равно 10a+b. Если цифры поменять местами, получится число 10b+a. Так как при увеличении числа на 75% оно умножается на коэффициент  , то справедливо соотношение
, то справедливо соотношение  или
или  . Соответствующие цифры легко подбираются.
. Соответствующие цифры легко подбираются.
Ответ: 12, 24, 36, 48.
Пример 4
Найдите все простые k, для каждого из которых найдется натуральное число n такое, что дробь  сократима на число k.
сократима на число k.
Решение.
Прежде всего заметим, что если дробь сократима, то числитель имеет общий множитель с одним из множителей знаменателя.
Докажем, что числитель  не может иметь общих простых делителей с первым множителем знаменателя
не может иметь общих простых делителей с первым множителем знаменателя  . В самом деле, разность этих чисел равна 7, и таким общим множителем может быть только простое число 7. Но тогда число n2 должно иметь остаток 3 при делении на 7, что невозможно. Для проверки этого можно, как показано в первом параграфе, рассмотреть квадраты всех возможных остатков при делении на 7.
. В самом деле, разность этих чисел равна 7, и таким общим множителем может быть только простое число 7. Но тогда число n2 должно иметь остаток 3 при делении на 7, что невозможно. Для проверки этого можно, как показано в первом параграфе, рассмотреть квадраты всех возможных остатков при делении на 7.
Со вторым множителем знаменателя таким делителем может быть только простое число 3, т.к. разность числителя и этого множителя равна 9. Причем такое действительно возможно, если, например, n =1.
Поделив числитель на третий множитель знаменателя, мы получим тождество  . Если первая дробь в этом тождестве сократима, то сократима и последняя, причем на число 47.
. Если первая дробь в этом тождестве сократима, то сократима и последняя, причем на число 47.
Ответ:  ,
,  .
.
Пример 5
Найдите пары целых чисел (x, y), удовлетворяющих уравнению  .
.
Решение.
Квадратичная часть уравнения имеет отрицательный дискриминант, поэтому в произведение выражение преобразовать не удается. А вот сумму квадратов выделить можно.
Заданное уравнение запишем в виде  . Если сумма квадратов двух чисел равна 10, то эти числа
. Если сумма квадратов двух чисел равна 10, то эти числа  и
и  могут быть лишь числами: 1 и 3, -1 и -3, 3 и 1, -3 и -1. Решив соответствующие 4 системы уравнений получим ответ.
могут быть лишь числами: 1 и 3, -1 и -3, 3 и 1, -3 и -1. Решив соответствующие 4 системы уравнений получим ответ.
Ответ:  ,
, 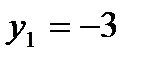 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
Пример 6
Разность двух натуральных чисел равна 32, а отношение наименьшего общего кратного и наибольшего общего делителя этих чисел равно 161. Найдите эти числа.
Решение.
Разность натуральных чисел делится без остатка на их наибольший общий делитель. Поэтому найдем все возможные значения наибольшего общего делителя и наименьшего общего кратного. Так как произведение натуральных чисел равно произведению их НОКа и НОДа, то получим несколько вариантов системы для определения искомых чисел.
Пусть искомые числа равны k и n=k+32. Так как разность натуральных чисел равна 25, то наибольшим общим делителем могут быть только числа: 1,2,4,8,16.32. Умножая квадраты этих чисел на 161, мы найдем, что произведение искомых чисел p соответственно равно: 161,644,2576,10304,41216. Для нахождения k получим квадратное уравнение  . Искомый корень
. Искомый корень  будет натуральным числом только при p =644.
будет натуральным числом только при p =644.
Ответ: 14 и 46.
Пример 7
Решите в натуральных числах уравнение  .
.
Решение.
Так как правая часть при натуральных z дает при делении на 4 остаток 1, то и левая часть должна давать такой же остаток при делении на 4, отсюда следует, что x четно. Пусть x=2m, где m -натуральное число. Аналогично, рассмотрим остатки обеих частей уравнения от деления на 3. Левая часть при всех натуральных x и y дает остаток 1, а 5 z дает остаток 1 только при четных z, откуда z=2k, где k -натуральное число. Тогда исходное уравнение можно переписать в виде  ,или
,или  .
.
Раскладывая левую часть по формуле разности квадратов, получаем  . Так как разложение правой части содержит только тройки, то каждая из скобок должна быть неотрицательной степенью тройки. Так как разность между скобками
. Так как разложение правой части содержит только тройки, то каждая из скобок должна быть неотрицательной степенью тройки. Так как разность между скобками  не делится на три, то это возможно только в случае, когда
не делится на три, то это возможно только в случае, когда  , а
, а  . Отсюда
. Отсюда  , а
, а  , или
, или  .
.
Еще раз применяя формулу разности квадратов, получаем  .
.
Значит оба сомножителя в левой части являются степенями двойки, отличающимися на 2. Следовательно,  ,а
,а  ,откуда m=1, а
,откуда m=1, а  , т.е. y=2. Тогда x=2 и 32+42=5z, откуда z=2.
, т.е. y=2. Тогда x=2 и 32+42=5z, откуда z=2.
Ответ: x=2, y=2, z=2.
Пример 8
Шесть простых чисел являются последовательными членами возрастающей арифметической прогрессии. Докажите, что разность этой прогрессии не менее 30.
Решение.
Предположим, что разность прогрессии нечетна. Тогда в этой прогрессии будет как минимум три четных числа, что невозможно. Аналогично, если разность прогрессии не кратна 3, то в этой прогрессии будут как минимум два числа, кратных трем. Значит, разность прогрессии кратна 2 и 3, т.е. кратна 6.
Если разность прогрессии не кратна 5, то в ней есть член, кратный 5. Тогда это просто число 5. Если 5 – первый член прогрессии, то среди оставшихся 5 членов есть еще один член, кратный 5, что невозможно. Если же 5 не является первым членом, то первый член будет отрицательным, ибо ранее доказано, что разность прогрессии не меньше 6.
Итак, разность прогрессии кратна 5 и 6, т.е. кратна 30, а значит, не менее 30.
|
|
|


