Интегрирование рациональных дробей

Производная вектор-функции по параметру

Определим производную вектор-функции по параметру:

.

Если производная в точке существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут .

Свойства производной вектор-функции (всюду предполагается, что производные существуют):

· — производная суммы есть сумма производных

· — здесь f(t) — дифференцируемая скалярная функция.

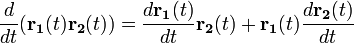· — дифференцирование скалярного произведения.

· — дифференцирование векторного произведения.

· — дифференцирование смешанного произведения.

 

Координаты нормали в точке поверхности
неявное задание
явное задание
параметрическое задание

Здесь .

Все производные берутся в точке .

 

 

В координатах уравнения касательной плоскости для разных способов задания поверхности приведены в таблице:

	касательная плоскость к поверхности в точке
неявное задание
явное задание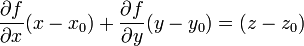
параметрическое задание

Все производные берутся в точке .

 

 

Непосредственное интегрирование

Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интегралов.

[править]Подведение под знак дифференциала

Данный метод эквивалентен методу замены переменной (см. далее):

[править]Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл Сделаем подстановку где — функция, имеющая непрерывную производную.

Тогда 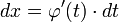и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

[править]Интегрирование выражений вида

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.

Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.

Если n и m чётные, то удобнее сделать подстановку tg x = t.

[править]Примеры

Вычислить:

Пусть тогда и

[править]Интегрирование по частям

Основная статья: Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:

Или:

В частности, с помощью n -кратного применения этой формулы находится интеграл

где — многочлен -ой степени.

 

 

Интегрирование рациональных дробей

Всякую правильную рациональную дробь , знаменатель которой разложен на множители

можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

где — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.

[править]Примеры

Вычислить:

Разложим подынтегральное выражение на простейшие дроби:

Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:

Следовательно

Тогда

Теперь легко вычислить исходный интеграл

 

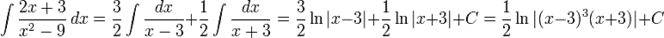
Площадь поверхности вращения, образованной вращением кривой вокруг оси можно вычислить по формуле

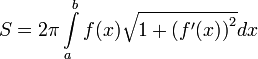
Площадь поверхности вращения, образованной вращением кривой вокруг оси можно вычислить по формуле

Для случая, когда кривая задана в полярной системе координат действительна формула

[править]

Поделиться:

Воспользуйтесь поиском по сайту: