 |
Методическая схема изучения признаков равенства треугольников
|
|
|
|
Систематический курс геометрии начнем изучать в 7 классе со знакомства с основными свойствами простейших геометрических фигур, которые сформулированы в виде аксиом.
№ 47, стр.23
АС и ВС пересекаются, т.е. точка В лежит в одной полуплоскости, а точка А – в другой (?)
 |
Точка В1
(АС) и лежит между точками А и С
Точка А1 (ВС) и лежит между точками В и С
Рассмотрим прямую (АА1), тогда точки А и С принадлежат разным полуплоскостям, т. к. отрезки АС и ВС пересекаются. Поэтому точки В и В1 (т.к. В1 лежит между С и А) лежат в разных полуплоскостях и, следовательно, АА1 
ВВ1
При решении используется понятие полуплоскости и аксиома IV (см. страница 8)
После изучения §1 учащимся даются понятия: аксиомы, теоремы, приводятся простейшие формы доказательств. (прочитать пункт 13 «аксиомы», страница 19) № 22 § 2, страница 32
 |
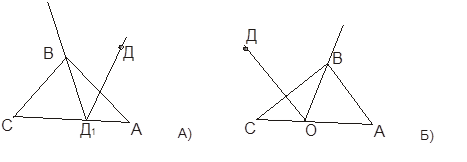Воспользуемся т. 1.1. (стр.17), согласно которой, из того что пересечена одна из сторон ∆ АВС (СА), прямая пересечет еще одну из оставшихся двух.
Рассмотрим 
ДОА. Если ДОА < АОВ, то луч ОД лежит между лучами АО и ОВ и, следовательно, пересекает отрезок АВ.
Если ДОА > ВОА, то луч ОД пересечет отрезок ВС (это связано
Следующими условиями: ВОА < ДОА и луч ОД лежит между лучами ОС и ОВ.
Методика изучения признаков равенства треугольников.
Изложение вопросов о равенстве треугольников во многом зависит от выбора определения равных треугольников. В учебнике Погорелова А.В. приводится гильбертовское определение равенства треугольников, которое требует выполнения шести равенств: трех для соответственных сторон треугольников и трех для соответственных углов этих треугольников. (смотри определение равенства на стр. 14)
|
|
|
Рассмотрим еще один вариант изложения темы равные треугольники:
1. Для равенства двух треугольников потребуем (по определению) равентсов трех соответствующих сторон этих треугольников;
2. В качестве аксиомы примем следующие утверждения: «Если две стороны и угол, заключенный между ними одного треугольника соответственно равны двум сторонам и углу заключенному между ними, другого треугольника, то такие треугольники равны».
Такой подход позволяет не доказывать третий признак равенства треугольников (это предусмотренно в 1.) и I признаках равенства треугольниках (это аксиома), что приводит к сокращению теоретического материала и упрощению логической структуры темы «Равенство треугольников», позволяет кратчайшим путем ввести один из основных методов традиционно-синтетической геометрии – метод равных треугольников.
Методика изучения первого признака равенства треугольников. Методическая схема по Погорелову А.В.:
1. Построить два треугольника, у которых равны две пары соответствующих сторон и углы, заключенные между ними;
2. На основании полученного рисунка сформулируйте теорему записать ее условие и заключение;
3. Сообщить идею доказательства;
4. Сообщить план доказательства;
5. Провести доказательство с четким выделением его шагов;
6. Осуществить закрепление его доказательства;
7. Рассмотреть с учащимися задачи на примере признака.
 |
Итак, пусть по сторонам В, С и углу А с помощью транспортира и линейки построено два треугольника: ∆ АВС и ∆ А1В1С1
Что можно сказать о ∆ АВС и ∆ А1В1С1 ?
После о том, что эти треугольники равны, формулируем теорему. Выясняем: что дано в этой теореме, а что надо доказать. Рядом с рисунком 1 краткую запись теоремы:
Дано: АВ =А1В1; АС=А1С1; 
А = А1
Доказать: ∆ АВС = ∆ А1В1С1
Сообщаем ученикам идею доказательства: рассмотреть третий ∆ А1В2С2, который: 1. равен ∆ АВС и расположен таким образом, что 2. его вершина В2 лежит на полупрямой А1В1; 3. вершина С2 находится в той же полуплоскости относительно прямой А1В1, в которой лежит вершина С1.
|
|
|
Теорема будет доказана, если установлено, что ∆ А1В2С2 совпадает с ∆ А1В1С1.
Составляем план доказательства:
1. Рассмотрим ∆ А1В2С2, о котором говорилось выше;
2. Докажем, что вершина В2 совпадает с вершиной В1;
3. Докажем, что луч А1С2 совпадает с лучом А1С1;
4. Докажем, что вершина С2 совпадает с вершиной С1;
5. Сделаем заключение о равенстве ∆ АВС и ∆ А1В1С1.
Приводим краткую запись доказательства на доске (оно выполняется учителем по ходу изложения, записывать доказательство в тетрадях не нужно),
1) ∆ А1В2С2 = ∆ АВС аксиома IV3
2) т.к. А1В1 = А1В2, то В2 совпадает с В1 аксиома IV1
3) т.к. В1А1С1 = В2А1С2, то лучи А1С2 и А1С1 совпадают
аксиома IV2
4) т.к. А1С1 = А1С2, то точки С2 и С1 совпадают аксиома IV1
5) ∆ А1В2С2 и ∆ А1В1С1 совпадают п.п. 2,4
6) ∆ АВС = ∆ А1В1С1 п.п. 5,1
Вопросы для закрепления
1. Как был выбран ∆ А1В2С2?
2. Почему вершина В2 совпадает с вершиной В1?
3. Зачем нужно доказывать совпадения лучей А1С2 и А1С1 ?
4. Почему вершина С2 совпадает с вершиной С1 ?
5. Почему делается вывод о равенстве ∆ АВС и ∆ А1В1С1
Рассмотрим еще одну методическую схему изучения этого признака:
1. рассмотреть решение ряда подготовительных задач;
2. доказать первый признак рав-ва треугольников.
Подготовительные задачи:
1) отрезки А1В1 и А1В2 равны отрезку АВ и отложены на полупрямой А1В1. Что ещё можно сказать о расположении отрезков А1В1 и А1В2 ?
2) Углы В1А1С1 и В1А1С2 равны углу А. Что можно сказать о расположении углов В1А1С1 и В1А1С2 ? Что можно сказать о расположении лучей А1С1 и А1С2, если они находятся в одной полуплоскости относительно прямой А1В1?
3) Треугольники А1В1С1 и А1В2С2 равны, вершина В2 лежит на полупрямой А1В1, вершина С2 лежит в одной полуплоскости (относительно прямой А1В1) с вершиной С1. Докажите, что эти треугольники совпадают, т.1. вершина В2 совпадают с вершиной В1, вершина С2 – с вершиной С1.
Рассмотренная первой методическая схема доказательства основана на применении репродуктивного метода обучения и он наиболее эффективен при изучении третьего признака равенства треугольников, наиболее сложного.
|
|
|
Схема решения задач па данной теме:
1) ученики читают задачу один – два раза, выполняют рисунок, записывают условие и требования задачи. Рассказать о требованиях к построению чертежей при решении задач по планеметрии.
2) Учитель направляет разбор задачи вопросами: “Что дано в задаче?”, “Что говорится о таком – то треугольнике?”, “Что ещё дано?”, “Что требуется выполнить в задаче?”, “С чего начнем выполнение рисунка?”, “Что ещё надо нарисовать?” и т. д.
3) Далее приступаем к поиску решения задачи:
 |
Рассмотрим некоторые задачи. №5, §3, стр.45
Дано: 
Доказать: 
Доказательство:
У данных треугольников есть по одной равной паре соответствующих сторон и одному равному углу прилежащему к этой стороне. Для док-ва рав-ва треугольников по II признаку следует найти ещё пару равных углов 
- как вертикальные 
по II признаку рав-ва треугольников.
№32, §3, стр.47 Дано: А, В, С, Д лежат на одной прямой; 
Доказать: 
 |
Доказательство:
1) 
;
2) 
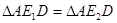- по I признаку равенства треугольников;
3) 
;
4) 
- по I признаку равенства треугольников;
 |
№39, §3, стр.48
Дано:
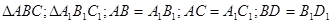Доказать: 
Доказательство:
1) 
(по условию); 
(по условию); 
- по III признаку равенства треугольников;
2) 
;
3) 
- по I признаку равенства треугольников;
4) 
и 
- по III признаку равенства треугольников;
Ч.т.д.
Заключение
Традиционно-синтетические аспекты занимают ведущее положение в геометрии, служат основой изложения остального материала, способствуют формированию пространственного представления и воображения учащихся (недаром некоторые разделы традиционно-синтетической геометрии(параллельность, перпендекулярность прямых и плоскостей, жесткость треугольника) называют “строительной геометрией”).
Придавая темам: параллельные и перпендикулярные прямые, признаки равенства треугольников, свойства равнобедренного и равностороннего треугольников, окружность, описанная около треугольника (вписанная в треугольник), задача на построение; четырёхугольники, правильные многоугольники, излагаем традиционно, максимальные образовательные цели, можно увидеть в них начала систематического курса геометрии.
|
|
|
В качестве вспомогательного математического метода к традиционно-синтетическому рассматривается координатно-векторный метод. Подготовка к вспомогательному методу выражается в раннем введении системы координат в ознакомлении учащихся с примерами решения задач координатным или векторно-координатным методом, в использовании формул расстояния между точками, если отказаться от координатно-векторного метода. Одновременное введение традиционно-синтетического и координатного методов в начале курса может быть обеспечено применением аксиоматически смешанного типа, причем неизбежно избыточной. Аксиоматику, в этом случае, следует рассматривать как инструмент рационализации логико-математической системы учебника.
Литература
1. К.О. Ананченко «Общая методика преподавания математики в школе», Мн., «Унiверсiтэцкае»,1997г.
2.Н.М.Рогановский «Методика преподавания в средней школе», Мн., «Высшая школа», 1990г.
3.Г.Фройденталь «Математика как педагогическая задача»,М., «Просвещение», 1998г.
4.Н.Н. «Математическая лаборатория», М., «Просвещение», 1997г.
5.Ю.М.Колягин «Методика преподавания математики в средней школе», М., «Просвещение», 1999г.
6.А.А.Столяр «Логические проблемы преподавания математики», Мн., «Высшая школа», 2000г.
|
|
|
12 |
