 |
Технология выбора эффективных тактик преподавателя при моделировании процесса обучения
|
|
|
|
С.П. Вовк
Представим процесс обучения в виде последовательности моментов управления tj, j=1,N. Моделирование взаимодействия "педагог-студент" в момент контроля знаний по j порции учебного материала в условиях несовпадающих многокритериальных оценок предлагается провести с использованием аппарата четких и нечетких игр. При представления ситуации обучения в виде игровой ситуации предлагается следующий алгоритм поиска оптимальных (или эффективных) тактик.
1. Представить схему взаимодействия "педагог-студент" в виде дерева позиционной игры.
2. Выявить множества тактик педагога A1 и студента A2.
3. Произвести оценку исходов партий на универсальной шкале результатов обучения wiÎWUN. Исходы оцениваются по степени достижения локальной цели обучения. Для представителей одного класса локальная цель представляется в виде некоторого диапазона рейтинг-чисел
4. Перейти к п.5 при возможности однозначной оценки исходов всех партий. Перейти к п.7. в случае неоднозначности оценки некоторых исходов, т.е. исходов, оцененных преподавателем в виде нечеткого интервала [b1,b2].
5.Определяются ожидаемые выигрыши игроков /1/
,
где Gi (a1,a2) - ожидаемый выигрыш при стратегии преподавателя a1Î A1, стратеги студента a2Î A2 и случайном ходе h. p(h) определяются в ходе педагогического эксперимента.
6. Представить схему взаимодействия в виде матричной формы игры /1/
Г=(A1,A2,G1,G2).
Поиск оптимальных решений осуществить с использованием традиционных методов решения матричных игр: при наличии "седловой точки" в матрице G существует решение в чистых стратегиях, при ее отсутствии - решение в смешанных стратегиях. Перейти к п.45.
7. Представить различную результативность достижения цели при использовании в позиционном дереве i уровней сложности заданий (“малая”, ”средняя”, ”высокая”) в виде соответствующих исходов 0,6 i, 0,8i, 1i на шкале оценок i уровня сложности заданий, т.е. в виде нечетких чисел b.
|
|
|
8. Произвести перевод исходов, представленных педагогом-экспертом в виде нечетких интервалов [b1,b2], и нечетких чисел b на единую шкалу оценки результата WUN. Аппроксимировать нечеткие интервалы [b1, b2]UN и нечеткие числа bUN с помощью S-образных функций принадлежности mw на единой шкале оценки результата WUN.
9. Представить на единой шкале результата итервалы [b1,b2]сjUN, соответствующие промежуточным целям для представителей классов.
10. Произвести аппроксимацию с помощью S-образных функций принадлежности mcj.
11. Определить степени уверенности преподавателя в том, что истинным состоянием студента является cj, j=1,m, определив возможность его классификации каждым из существующих классов C={c1,...,cm} с помощью степени разделения нечетких множеств mw и mcj. Описание свойства, что результат есть [b1,b2]сjUN описать уравнением назначения возможности Пm = [b1,b2]сjUN. Определить по реальному результату студента w,описываемому функцией принадлежности mw, меру возможности Пm с помощью соотношения /5/
Пcj(w)=POSS(m есть w| m есть cj)=sup(mwÙ mcj). wÎWUN
12. Упорядочить состояния, в которых может находиться студент, по убыванию их вероятностей p(c1)³...³ p(cm). Оценить степень истинности утверждения a=“состояния C упорядочены по убыванию вероятности” /3/ как Т(a)=1.
13. Определить полезности u(w=0,6i), u(w =0,8i), u(w =1i) на шкале результата Wi, соответствующей уровню сложности задания i, путем экспертного опроса преподавателя.
14. Выбрать дерево позиционной игры, описывающее взаимодействие “педагог-студент” для обучаемого класса c1.
15. Определить полезности uf для " af ÎA1. Тактика af представляет последовательность заданий различных уровней сложности во время каждой из k попыток общения со студентом af =d1,...,d3, где dk - k -ый ход преподавателя.
|
|
|
16. Построить функцию полезности результата U(w) на универсальной шкале wÎWUN как нижнюю границу на множестве полезностей тактик
{uf} 
17. Построить зависимость функции полезности результата для каждого из возможных состояний студента cjÎC, j=1,m. Для этого m раз выполнить п.15-16 для позиционных деревьев, описывающих взаимодействие педагог со студентом соответствующего класса.
18. Определить на на парах "действие-состояние” позиционного дерева, с помощью которого производится моделирование взаимодействия между педагогом и студеном при контроле знаний по j порции учебного материала,, предпочтения педагога /3/ ufj =u(af,cj) относительно тактик af ÎA при условии, что истинным состоянием обучаемого является принадлежность к классу cj, используя ранее определенную зависимость функции полезности.
19. Произвести анализ тактик преподавателя с помощью отношения четкого доминирования по полезности. Если все тактики можно упорядочить с помощью четкого доминирования по полезности перейти к п.44. Если среди тактик существует хотя бы одна af четко доминирующая над остальными, то принять mД (ag,af)=0 "agÎA1 и перейти к п.29. Если отношение четкого доминирования по полезности не позволяет упорядочить тактики, перейти к п.20.
20. Задать нечеткие оценки полезности ufj и ugj в виде нечетких чисел с соответствующими функциями полезности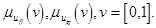 
для пары сравниваемых тактик (af,ag) "af,agÎA1.
21. Определить нечеткие числа, описывающие полезности, в виде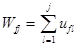 
.
22. Оценить истинность утверждения bj’=<Wfj³Wgj> с помощью пересечения нечетких множеств /3/
23. Определить степень доминирования af над ag /3/ как
24. Оценить истинность утверждения bj”=< Wgj³Wfj> с помощью пересечения нечетких множеств /3/
25. Определить степень доминирования 
26. Оценить истинность утверждения /3/
27. Определить степень доминирования /3/ mД (af,ag)=min{T(a),T(b)}.
28. Произвести попарный анализ тактик преподавателя, выполнив п. 20-23.
29. Построить нечеткое множество недоминируемых тактик преподавателя AНД1 с функцией принадлежности принадлежности /3/ mНД (af)= 1 - max mД (ag,af), af Î A1 agÎA1
30. Построить нечеткое множество недоминируемых тактик студента AНД2, для чего выполнить п.11-29 алгоритма на множестве тактик студента A2, рассматривая в качестве возможных состояний природы наборы заданий njÎN, которые им предлагает для выполнения преподаватель. Т.е. задача анализа тактик задается отображением a: N®W.
|
|
|
31. Определить нечеткость исхода /2/ на A1´A2={((a1,a2),s1(a1)Ùs2(a2))}, a1ÎA1, a2Î A2, где нечеткость стратегии si:Ai®[0,1] задается с помощью отношения строгого доминирования и описывается функцией принадлежности mНД1 (af) и mНД2(af).
32. Построить матрицу CL1, задающую степень важности критерия lÎ L1. для студента класса c. Матрица строится на основе данных, полученных при опросе педагогов-экспертов.
33. Построить матрицу L1A1, задающее степень соответствия критерия l тактике a.
34. Построить матрицу Q1, отражающую агрегированные предпочтения преподавателя относительно тактики a для студента с, элементы которой описываются с помощью функции принадлежности /4/
.
35. Определить порог разделения зон тактик преподавателя /4/, построив попарное пересечение агрегированных предпочтений для тактик ai,ajÎA1
h1£min max min{mqi(c,ai),mqj(c,aj)}
ij c
36. С помощью текстового опроса выявляется множество критериев L2, которые учитывает студент класса с при выборе тактики взаимодействия с преподавателем.
37. Построить матрицу NL2, отражающую предпочтения студента класса с относительно тактики аÎA2, если студенту предложено задание n, на основе результатов текстового опроса студентов разных классов cÎC о сложности и содержании заданий nÎN, которые бы они выбрали в реально складывающейся ситуации обучения.
38. Построить матрицу L2A2, отражающую степени соответствия критериев, принимаемых во внимание при ПР, с тактиками взаимодействия с конкретным преподавателем на основе результатов опроса.
39. Построить матрицу Q2, отражающую агрегированные предпочтения студента относительно выбора тактики aÎA2 при выдаче преподавателем задания n, элементы которой описываются с помощью функции принадлежности 
.
40. Определить порог разделения зон тактик студента, построив попарное пересечение агрегированных предпочтений для тактик ai,ajÎA2
|
|
|
h2£min max min{mqi(n,ai),mqj(n,aj)}
ij n
41. Построить на нечетком множестве исходов W= A1´A2={(a1,a2),s1(a1)Ùs2(a2))}, a1ÎA1, a2 ÎA2 четкое отношения уровня Rhi={(a1,a2)ÎA1´A2|R(a1,a2)³hi }с характеристической функцией Rhi=1, если R(a1,a2)³hi, и Rhi =0, если R(a1,a2)<hi.
42. Найти равновесное решение игры /2/ как Rh1ÙRh2.
43. Пары
{(a1*,a2*)ÎA1´A2|R(a1,a2)=1 }являютя оптимальными тактиками соответственно преподавателя и студента.
44.Определить ожидаемые полезности /3/ оптимальных тактик 
45. Конец
Алгоритм предлагается использовать для определения оптимальных или эффективных тактик преподавателя в реально складывающихся ситуациях обучения, в которых у преподавателя при принятии решения о выборе наиболее подходящего педагогического воздействия возникает проблема мнгокритериального оценивания результата обучения. За счет выбора для обучения “лучшего” сценария предлагаемая технология позволяет произвести моделирование процесса взаимодействия “педагог-студент” для конкретного студента с учетом предыстории его обучения и личностных особенностей. Для моделирования взаимодействия в конкретной игровой ситуации предлагается использовать аппарат четких и нечетких игр в зависимости от ограниченности информации, требующейся преподавателю для принятия решения.
Список литературы
Дж.Нейман, О.Моргенштерн Теория игр и экономическое поведение. - М.: Наука, 1970. - 707с.
R.K.Ragade Fuzzy games in the analysis of options. - Journal of Cybernetics, 1976, v.6, h.213-214.
Обработка нечеткой информации в системах принятия решений/ А.Н.Борисов, А.В.Алексеев, Г.В.Меркурьева и др. - М.: Радио и связь, 1989. - 304с.
Й.Леунг Разделение на торговые зоны в нечетких условиях/Теория возможностей и ее применение -М.:Наука,1991г.
Э.Санчес, Ж.Гуверне, Р.Бартолен, Л.Вован Лингвистический подход к нечеткой логике воз-классификации диспротеинемии / Теория возможностей и ее применение. М: Наука, 1992.
|
|
|
