 |
Краткие теоретические и практические сведения
|
|
|
|
Лабораторная работа № 1
Изучение линейных цепей постоянного и переменного тока
Цель работы: экспериментальная проверка выполнения законов Ома и Кирхгофа для неразветвленной и разветвленной электрических цепей постоянного тока; исследование амплитудных и фазовых соотношений между напряжениями и токами для R, L, C – элементов
Краткие теоретические и практические сведения
Электрической цепью называют совокупность устройств и объектов, соединенных определенным образом и образующих путь для протекания электрического тока. Электромагнитные процессы в электрических цепях могут быть описаны с помощью понятий об ЭДС, токе и напряжении.
Для анализа и расчета электрическую цепь представляют в виде электрической схемы, содержащей условные обозначения ее элементов и способы их соединения. Электрическая схемапредставляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи. Электрическую цепь, которая оснащена не менее чем одним электронным элементом, называют электронной цепью.
Все устройства и объекты, входящие в состав электрической цепи, могут быть разделены на три группы: источники электрической энергии (питания); потребители (приемники) электрической энергии; вспомогательные элементы цепи.
Электрические цепи классифицируют по различным признакам:
- по роду тока - постоянного тока, переменного тока, синусоидальные, несинусоидальные;
- по характеру элементов: линейные (в них все элементы линейные), нелинейные (содержат хотя бы один нелинейный элемент);
- по числу фаз: однофазные, трехфазные.
|
|
|
При расчете в схеме электрической цепи выделяют несколько основных элементов.
Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током, состоящий из одного или нескольких последовательно соединенных элементов.
Узел электрической цепи (схемы) – место (точка) соединения трех и более ветвей.
Соединение, при котором все ветви (участки) цепи присоединены к одной паре узлов, называют параллельным. При параллельном способе соединения каждая из ветвей находится под одним и тем же напряжением.
Приемники могут быть соединены друг с другом последовательно, параллельно и смешанно.
При последовательном соединении по всем элементам протекает один ток, поэтому сопротивление участка с последовательным соединением элементов можно заменить одним – эквивалентным равным сумме всех элементов. Условие эквивалентности такой замены заключается в том, что при этом состояние других элементов, которые не подвергались замене, не должно измениться (токи, напряжения, мощности не должны измениться).
При параллельном соединении нескольких элементов (ветвей) ко всем элементам (ветвям) приложено одно и тоже напряжение. Эквивалентное сопротивление при параллельном соединении нескольких приемников (например, для двух), определяется по формуле.
RЭ = 
. (1.1)
Цепи, в которых элементы или ветви соединены последовательно и
параллельно называют цепями со смешанным соединением элементов. При смешанном соединении, например, трех элементов (R1 соединено последовательно с параллельным участком, R2 и R3) эквивалентное сопротивление определяется по формуле:
. (1.2)
Контур - образован ветвями и узлами, которые образуют замкнутый путь для протекания электрического тока.
Схема с последовательным соединением элементов образует один контур и называется одноконтурной. Схема со смешанным соединением элементов, в общем случае образует несколько контуров и называется многоконтурной схемой.
|
|
|
Под расчетом (анализом) электрической цепи понимают нахождение токов во всех ветвях схемы. Все расчеты электрических цепей основываются на физических законах, к числу которых относятся законы Ома, Кирхгофа и Джоуля-Ленца.
Закон Ома устанавливает связь между током, напряжением и параметрами элементов в электрической цепи и позволяет рассчитывать в них токи.
Закон Ома для участка цепи не содержащего источников ЭДС -
сила тока в участке цепи прямо пропорциональна напряжению на
концах этого участка и обратно пропорциональна его сопротивлению:
I =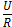 
. (1.3)
Закон Ома для полной (замкнутой) цепи – сила тока в цепи прямо пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника:
I = 
. (1.4)
Законы Кирхгофа.
Первый закон Кирхгофа устанавливает связь между токами, сходящимися в узле электрической цепи: алгебраическая сумма всех токов, сходящихся в узле, равна нулю
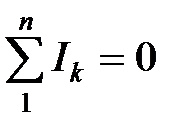(1.5)
где n — число ветвей, подключенных к узлу. Равнозначной является другая формулировка: сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут с одним знаком, обычно со знаком «плюс», а токи, направленные от узла, - со знаком "минус" или наоборот.
Второй закон Кирхгофа у станавливает связь между напряжениями на элементах контура электрической цепи:
алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех участках (элементах) контура
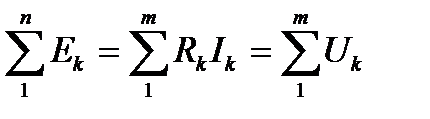, (1.6)
где n — число источников ЭДС в контуре, m — число элементов с сопротивлением Rkв контуре, Uk = RkIk — напряжение или падение напряжения на k-м элементе контура.
Для записи уравнений по второму закону Кирхгофа необходимо:
- задать условные положительные направления ЭДС, токов и напряжений;
- выбрать положительное направление обхода контура, для которого записывается уравнение;
- записать уравнение, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с направлением обхода контура, и со знаком «минус», если они противоположны.
|
|
|
Важную роль для проверки правильности расчетов любых электрических цепей играет условие баланса мощностей, которое следует из закона сохранения энергии и может быть сформулировано следующим образом:
алгебраическая сумма мгновенных мощностей всех источников энергии в электрической цепи равна алгебраической сумме всех мгновенных мощностей всех приемников цепи:
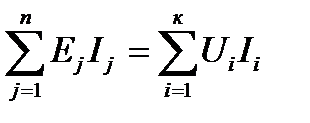(1.7)
где Еj, Ij – напряжение и ток j – того источника; Ui, Ii – напряжения и ток i – того элемента цепи.
Мощность любого элемента электрической цепи, будь то источник или приемник, определяется как произведение тока элемента и напряжения на нем: P = UI.
Для цепей постоянного тока, содержащих источники энергии и резисторы, выражение (1.6), можно записать в следующем виде
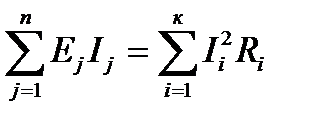(1.8)
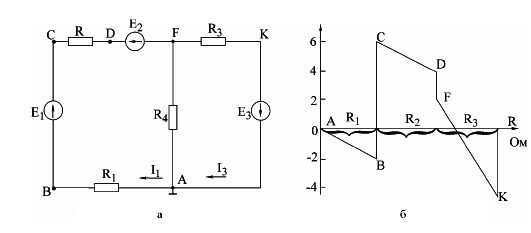
Потенциальная диаграмма – представляет собой графическую интерпретация второго закона Кирхгофа для контура и представляет собой график распределения потенциала вдоль замкнутого контура электрической цепи. Для построения диаграммы на оси абсцисс откладываются значения сопротивлений участков цепи в последовательности их обхода по контуру, а на оси ординат — потенциалы соответствующих точек. По диаграмме можно найти разность потенциалов (напряжение) между двумя любыми выбранными точками контура. Пример построения потенциальной диаграммы:
Резистор, конденсатор и катушка индуктивности в цепи переменного тока.
В цепи переменного тока, изменяющегося по синусоидальному закону (в дальнейшем переменного тока), используются следующие элементы и определения: резистор, активное сопротивление; индуктивность, индуктивное сопротивление; емкость, емкостное сопротивление; фаза, начальная фаза, угол сдвига фаз; период, частота, угловая частота; мгновенное, действующие и средние значения гармонических величин; активные, реактивные, комплексные сопротивления и проводимости; полная, активная, реактивная, комплексная мощности.
Действующее (среднеквадратичное) значение тока I равно:
= 
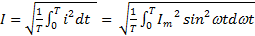= 0.707 I m, (1.9)
где i =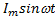 
– мгновенное значение, Im – амплитудное значение, Т – период синусоидального тока. Аналогично U=Um/ 
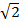; E=Em/ 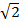. Отношение ka = Im / I = 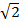называется коэффициентом амплитуды.
|
|
|
Под действующим значением синусоидального тока понимают такой ток, который за время, равное периоду, выделяет такое же количество тепла, что и эквивалентный ему постоянный ток.
Под средним значением синусоидального тока понимают его среднее значение за период:
Iср = 
. (1.10)
Отношение действующего значения периодически изменяющейся функции к ее среднему значению называют коэффициентом формы kф. Для синусоидального тока коэффициент формы:
= 1.11. (1.11)
Резистор в цепи постоянного и переменного тока в любой момент времени обладает одним и тем же значением активного сопротивления R = U/I. Ток и напряжение совпадают по фазе. Угол сдвига фаз между напряжением и током равен нулю, поэтому активное сопротивление резистора не зависит от частоты:
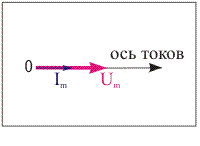
В символической (комплексной) форме закон Ома для действующих значений всех величин в общем случае запишется:
= 
,
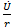где r – комплексное сопротивление (комплекс) резистора равное его модулю, r=R.
Для действующих значений по результатам измерений закон Ома
I R = U.
Среднее значение мощности, рассеиваемой на резисторе
Pср.=U×I= Um××Im/2. (1.12)
Катушка индуктивности – элемент электрической цепи переменного тока в котором накопление энергии происходит в электромагнитном поле. В электрической цепи с идеальной индуктивной катушкой пренебрегают нагреванием витков, поэтому ее активное сопротивление rk = 0. Ток отстает по фазе от напряжения на угол 900:
Сопротивление идеальной катушки XL =ω L = 2π fL, Ом, прямо пропорционально частоте. Здесь L – индуктивность катушки.
Закон Ома для действующих значений тока и напряжения для цепи с идеальной индуктивной катушкой в комплексной форме:
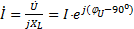, (1.13)
где jXL – комплекс реактивного индуктивного сопротивления.
В цепи, содержащей катушку индуктивности, происходит периодический обмен энергией между генератором и катушкой без необратимого преобразования электромагнитной энергии, т.е. среднее за период значение мощности цепи с идеальной катушкой P ср. = 0. Следовательно, индуктивная катушка является
реактивным элементом, а мощность, эквивалентная энергии обмена – реактивной:
QL=XL ×I2, ВАр. (1.14)
Все реальные катушки индуктивности обладают активным сопротивлением rk (эквивалент тепловой энергии, выделяющейся при протекании тока по виткам провода катушки, подводящих проводови т. д.). Такую реальную индуктивную катушку можно представить из последовательно соединенных идеальных элементов: идеальной индуктивной катушки Lk и резистивного элемента с активным сопротивлением rk.
|
|
|
При напряжении на зажимах реальной катушки, изменяющемся по закону u = Um ⋅ sin(ω t + ju), по ней протекает ток, изменяющийся по закону i = Im ⋅ sin(ω t + ji). Ток отстает по фазе от напряжения на угол ji=ju − jk, который из-за наличия в катушке активного сопротивления rk всегда меньше 90°. Угол сдвига фаз между напряжением и током j = jk определяется из треугольника сопротивлений по формуле: j = arctg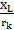 
.
Сопротивление реальной индуктивной катушки в комплексной форме:
, (1.15)
где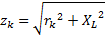 
– модуль комплекса полного сопротивления реальной индуктивной катушки; j – его аргумент.
Закон Ома для действующих значений тока и напряжения в комплексной форме: 
.
Активная мощность в реальной индуктивной катушке:
P = U ⋅ I ⋅ cosj =Ur ⋅ I = rk ⋅ I2 , Вт, (1.16)
где cosj – коэффициент мощности, показывающий, какая часть электрической энергии была преобразована в другой вид.
Реактивная мощность в индуктивной катушке:
Q = U ⋅ I ⋅ sinj = 
⋅ I = XL ⋅ I2, Вар. (1.17)
Конденсатор – элемент электрической цепи переменного тока, в котором процесс обмена происходит посредством электрического поля. В качестве элемента, обладающего емкостью, используется конденсатор.
При напряжении на зажимах конденсатора, изменяющемуся по закону u = Um ⋅ sin(ω t + ju), по цепи с конденсатором протекает ток, изменяющийся по закону i = Im ⋅ sin(ω t + ji). Ток опережает напряжение по фазе на угол сдвига фаз, равный 90°. Фаза тока ji = ju + 90°:
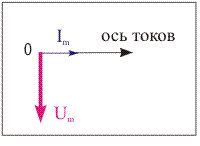
Сопротивление идеального конденсатора переменному току является эквивалентом электрической энергии, которой обмениваются емкость и источник, называется реактивным емкостным сопротивлением и определяется по формуле: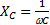 
,
где С – емкость конденсатора; ω – угловая частота. Величину емкостного сопротивления можно рассчитать по формуле Xc = U/I, предварительно измерив напряжение на конденсаторе U и силу переменного тока в цепи I.
Закон Ома в комплексной форме для действующих значений тока и напряжения для цепи с идеальным конденсатором:
= 
,
где (− jXc) – комплексное емкостное сопротивление.
Среднее значение мощности за период в цепи с идеальным конденсатором равно нулю, Pср. = 0. Реактивная емкостная мощность, эквивалентная энергии обмена, обозначается QC и определяется по
формуле:
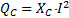, (Вар). (1.18)
1.2. Описание лабораторного макета
Электрческие схемы исследуемых цепей представлены на рис. 1.1 и 1.2
Рис. 1.1. Линейная электрическая цепь постоянного тока: а) с последовательным соединением приемников; б) со смешанным соединением приемников.
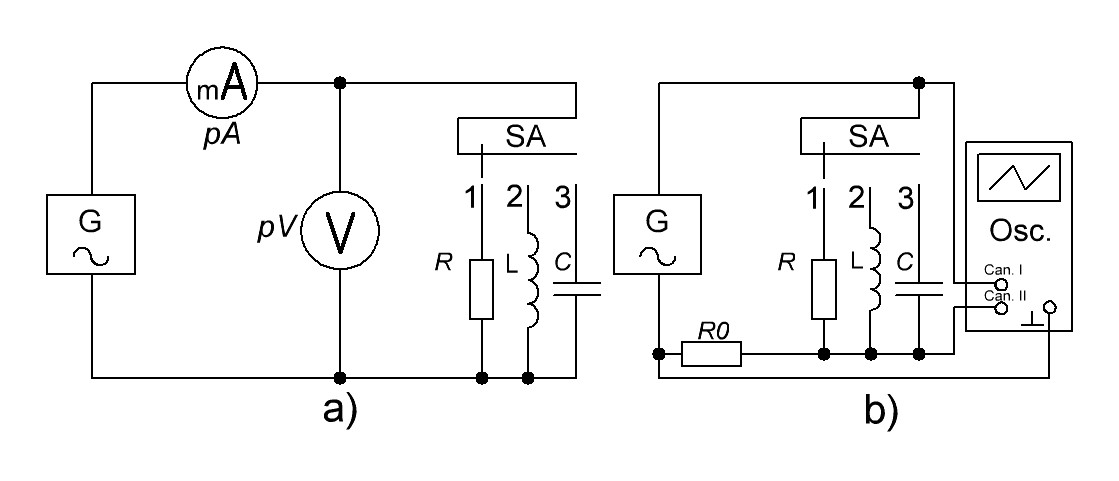
Рис. 1.2. Электрическая цепь переменного тока: а) для определения параметров R, L, C – элементов б) для исследования амплитудных и фазовых соотношений межу током и напряжением элементов.
Для измерения тока и напряжения в исследуемых схемах используются цифровые мультиметры типа ДТ9205 в соответствующем режиме работы. В качестве источника ЭДС служит лабораторный блок питания постоянного тока с регулируемым и стабилизированным напряжением. В схемах рис.1.2 применяются генератор гармонических сигналов Г3-112 и двухканальный осциллограф СI-83. Подсоединение источника питания Е и мультиметров к схемам осуществляется при помощи соединительных проводников, а генератора и осциллографа при помощи коаксиальных кабелей. При анализе полученных результатов следует учесть погрешности измерения измерительных приборов.
|
|
|
12 |
