 |
Механизмы с гибкими звеньями
|
|
|
|
Кинематика винтовых механизмов
В технических системах более всего распространены винтовые механизмы, выполненные по схеме, представленной на рис. 6, б. Зависимость линейного перемещения ℓ2 ведомой гайки от угла поворота j1 винта (функция положения) имеет вид
, (6)
где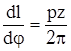 
– передаточная функция, или аналог скорости передачи винт-гайка.
Линейная скорость ведомой гайки
v2 = dl2 / dt =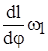 
, (6)
где w1 = dj1/dt – угловая скорость винта.
Для снижения скорости линейного перемещения гайки при заданной угловой скорости винта w1 уменьшают шаг резьбы р и число ее заходов z принимают равным 1. Скорость перемещения гайки v2 можно уменьшить за счет снижения угловой скорости винта w1 с помощью червячной или многоступенчатой зубчатой передачи (редуктора). Эти редукторы устанавливают между двигателем и передачей винт – гайка. Тогда w1 = wд / iд1, где iд1 – передаточное отношение зубчатого редуктора, wд – скорость вращения двигателя.
Механизм с дифференциальным винтом (рис. 6, д) имеет две винтовые пары с разными параметрами резьбы. В паре со стойкой 3 винт имеет резьбу с шагом р1 и числом заходов z1, а в винтовой паре с ведомой гайкой 2 – резьбу с шагом р2 и числом заходов z2. Аналог скорости поступательного перемещения в соответствующих винтовых парах будет соответственно равен 
и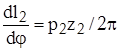 
. Функция положения, т.е. зависимость линейного перемещения гайки 2 от угла поворота винта, равна
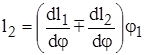, (7)
где знак минус относится к механизмам с винтом, имеющим резьбы одного направления винтовой линии, а знак плюс – к механизмам с винтом, имеющим резьбы в парах со стойкой 3 и гайкой 2 с разным направлением винтовой линии, например, правую и левую резьбы.
|
|
|
Длина нарезанной части винта Lb определяется по формуле
Lb=ℓmax+ℓr+Dℓ, (8)
где ℓmax – максимальное перемещение винта или гайки; ℓr – длина резьбы гайки; Dℓ – запас резьбы (2 … 3 витка).
Для обеспечения достаточной прочности и жесткости диаметр винта d выбирают из соотношения d ³ 0,05 Lb.
Механизмы с гибкими звеньями
Применяют для передачи вращательного движения между валами при больших межосевых расстояниях и для преобразования вращательного движения в поступательное и наоборот. Ведущее и ведомое жесткие звенья таких механизмов не имеют между собой непосредственного контакта, а передача движения осуществляется посредством гибкого звена, которое может быть как замкнутым, так и разомкнутым. По характеру соединения гибкого звена с ведущим и ведомым звеньями рассматриваемые механизмы подразделяют на передачи трением, передачи зацепления и передачи с жестким креплением гибкого звена к другим звеньям. В передачах трением в качестве гибкого звена используют плоские и клиновидные ремни, пассики, круглые шнуры и ремни, нити (рис. 9, а). Передача состоит из ведущего 1 и ведомого 2 шкивов, а также замкнутого звена 3, надетого на шкивы с натяжением. Таким передачам присущи все достоинства и недостатки фрикционных механизмов непосредственного касания. Необходимым условием нормальной работы передачи трением является натяжение гибкого звена, что достигается обычно при помощи натяжного ролика 4 (см. рис. 9). В передачах зацепления гибким звеном служит зубчатый ремень, перфорированная лента, цепь. Преимущества этих передач (см. рис. 9, б) перед передачами трением соответствуют преимуществам зубчатых передач по отношению к фрикционным.
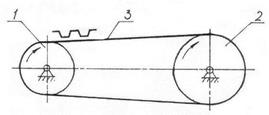
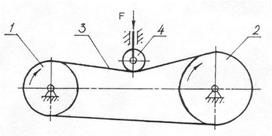
а б
Рис. 9
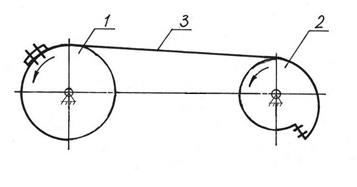
В передачах с жестким креплением разомкнутого гибкого звена к ведущему 1 и ведомому 2 звеньям (рис. 10) исключается возможность его проскальзывания, чем обеспечивается точность передачи. Недостатком таких передач является ограничение вращения ведущего и ведомого звеньев в одном направлении углом, меньшим 2π.
|
|
|
|
ЛИТЕРАТУРА
| 1 | Красковский Е.Я., Дружинин Ю.А., Филатова Е.М. Расчет и конструирование механизмов приборов и вычислительных систем: Учебное пособие. М.: – Высш. шк., 2001. – 480 с. | 2001 |
| 2 | Сурин В.М. Техническая механика: Учебное пособие. – Мн.: БГУИР, 2004. – 292 с. | 2004 |
| 3 | Ванторин В.Д. Механизмы приборных и вычислительных систем: Учебное пособие. – М.: Высш. шк., 1999. – 415 с. | 1999 |
|
|
|
