 |
Раздел 1. Развитие понятия о числе.
|
|
|
|
№1-10. Найти корни уравнения
1) 5y2 – 2y + 2 = 0
2) 2 + 18x2 = 0
3) x2 – 4x + 8 = 0
4) x2 – 2x + 5 = 0
5) 3z2 + 27 = 0
6) 5x2 – 2x + 1 = 0
7) x2 – 8x + 41 = 0
8) 7x2 + 343 = 0
9) x2 – 4x + 13 = 0
10) 0,5z2 – z + 13 = 0
Раздел 2. Степени, корни, логарифмы.
№ 11 -20. Найти значение выражения: 11) а) 
б) 
12) а)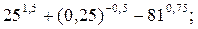 
б) 
13) а) 
б)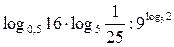 
14) а) 
б) 
15) а)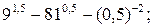 
б)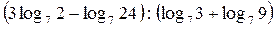 
16) а) 
б) 
17) а) 
б)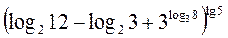 
18) а)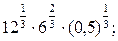 
б) 
19) а) 
б) 
20) а) 
б) 
Раздел 3. Прямые и плоскости в пространстве
№ 21-30 Решите задачу.
| 21) Найдите расстояние от середины отрезка АВ до плоскости, не пересекающей этот отрезок, если расстояния от точек А и В до плоскости равны 3,2 см и 5,3 см. |
| 22) Дан ∆ АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1 , а сторону ВС – в точке В1. Найдите длину отрезка А1В1 , если АВ = 15 см, АА1 : АС = 2: 3. |
| 23) Из точки к плоскости проведены две наклонные, равные 10 см и 17 см. Разность проекций этих наклонных равна 9 см. Найдите проекции наклонных. |
| 24) Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если АС = 6 м, ВD = 7 м, CD = 6 м. |
| 25) Параллельные плоскости α и β пересекают сторону АВ угла АВС в точках D и D1, а сторону ВС – в точках Е и Е1. Найдите длину отрезка DЕ, если ВD = 24, ВD1 = 36, D1Е1 = 46. |
| 26) Дан ∆ АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1, а сторону ВС – в точке В1. Найдите длину отрезка А1В1, если АВ = 8 см, АА1 : А1С = 5: 3. |
| 27) Отрезок АВ не пересекает плоскость, АС и ВD перпендикулярны этой плоскости, АС = 30 дм, ВD = 20 дм, СD = 24 дм. Найдите длину отрезка АВ. |
| 28) Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна из них на 26 см больше другой, а проекции наклонных равны 12 см и 40 см. |
| 29) Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС в точке D, а сторону ВС – в точке Е. Найдите длину стороны DЕ, если АВ = 15 м и АD: AC = 2: 5. |
| 30) Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если АС = 3 м, BD = 4 м, CD = 12 м. |
|
|
|
Раздел 4. Элементы комбинаторики
№ 31-40. Вычислите
31) 
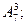
32) 
33) 
34) 
35) 
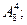
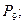
36) 
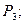
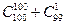
37) 
38) 
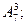
39) 
40) 
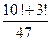
Раздел 5. Координаты и векторы.
№ 41 -50. Решить задачу:
41) Дано: 
(3; 1; -2) и 
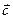(1; 4; -3)
Найти: 
.
42) Дано: 
(2; -1; 0), (-3; 2; 1) и 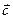(1; 1; 4)
Найти: координаты вектора 
.
43) Дано: (-1; 2; 0), (0; -5; -2) и 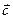(2; 1; -3)
Найти: 
.
44) Дано: (2; -1; 0), (-3; 2; 1) и 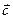(1; 1; 4)
Найти: координаты вектора 
.
45) Дано: (5; -1; 2) и (3; 2; -4)
Найти: 
.
46) Дано: (-1; 2; 0), (0; -5; -2) и 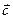(2; 1; -3)
Найти: координаты вектора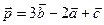 
.
47) Дано: (2; 4; -6), (-9; -3; 6) и 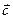(3; 0; -1)
Найти: координаты вектора 
.
48) Дано: (2; -1; 0), (-3; 2; 1) и 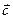(1; 1; 4)
Найти: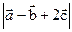 
.
49) Дано: (2; 4; -6), (-9; -3; 6) и 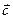(3; 0; -1)
Найти: координаты вектора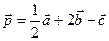 
.
50) Дано: (-1; 2; 0), (0; -5; -2) и 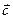(2; 1; -3)
Найти: координаты вектора 
.
Раздел 6. Функция.
№ 51 – 60. Описать виды преобразований функции и построить график.
51) у = 2(х – 1)2 + 3.
52) у = 
(х + 3)2 – 2.
53) у = (х – 1,5)2 + 2.
54) у = 3(х – 2)2 + 1.
55) у = 
(х + 1)2 – 3.
56) у = - (х + 2)2 – 1.
57) у = (х – 1)2 – 4.
58) у = 2(х + 2)2 – 2.
59) у = - (х - 3)2 + 4.
60) у = (х – 2)2 + 3.
Рабочая тетрадь № 2.
Разделы 7. Основы тригонометрии, 12. Уравнения и неравенства.
№ 1 – 10. Решить уравнения:
1) а) 
б) 
в) 
2) а) 
б) 
в) 
3) а) 
б) 
в) 
4) а) 
б) 
в) 
5) а)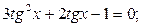 
б) 
в) 
6) а) 
б) 
в) 
7) а)
б)
в)
8) а)
б)
в)
9) а)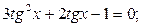
б)
в)
10) а)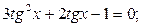
б)
в)
Раздел 10. Дифференциальное исчисление.
№ 11 -20. Исследовать функцию на монотонность.
| № задания | |
| 11) | 
|
| 12) | 
|
| 13) | 
|
| 14) | 
|
| 15) |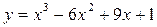 
|
| 16) |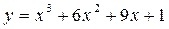 
|
| 17) | 
|
| 18) |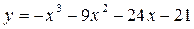 
|
| 19) | 
|
| 20) |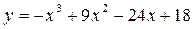 
|
Раздел 11. Интегральное исчисление.
|
|
|
№ 21-30. Решите задачу:
| № задания | |
| 21) | Скорость точки, движущейся прямолинейно, задана уравнением v = 6t2 – 4t – 10. Вычислить её путь за 4 с от начала движения. |
| 22) | Скорость точки, движущейся прямолинейно, задана уравнением v = 18t – 6t2. Вычислить её путь от начала движения до остановки. |
| 23) | Вычислить работу, совершенную при растяжении пружины на 0,06 м, если при растяжении её на 0, 01 м нужна сила 10 Н. |
| 24) | Скорость точки, движущейся прямолинейно, задана уравнением v = 6t2 – 10t. Вычислить её путь за четвёртую секунду. |
| 25) | Скорость точки, движущейся прямолинейно, задана уравнением v = 18t – 6t2. Вычислить её путь за 3 с от начала движения. |
| 26) | Вычислить работу, совершенную при растяжении пружины на 0,08 м, если при растяжении её на 0, 01 м нужна сила 10 Н. |
| 27) | Скорость точки, движущейся прямолинейно, задана уравнением v = 9t2 – 2t – 8. Вычислить её путь за 4 с от начала движения. |
| 28) | Вычислить работу, совершенную при растяжении пружины на 0,06 м, если при растяжении её на 0, 03 м нужна сила 15 Н. |
| 29) | Скорость точки, движущейся прямолинейно, задана уравнением v = 3t2 – 2t +5. Вычислить её путь за третью секунду. |
| 30) | Скорость точки, движущейся прямолинейно, задана уравнением v = 3t2 – 6t. Вычислить её путь от начала движения до остановки. |
|
|
|
