Исследование колебаний в резонансных цепях

2.1. Исследование последовательного колебательного контура.

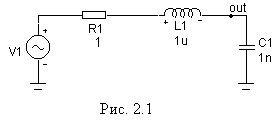
Введите схему последовательного колебательного контура по рис. 2.1. Параметры источника Sine source пока не важны, емкость С1 выберите произвольно из интервала 100р…3000р, индуктивность L1 из интервала 0.1u…5u. Постройте в режиме AC Analysis АЧХ (и в децибелах, т.е. db(v(C1)), и в разах, т.е. v(С1)) и ФЧХ контура, т.е. ph(v(C1)) и по ним найдите точную резонансную частоту контура f_p. Запишите f_p. Найдите по графикам и запишите ширину полосы пропускания контура П по уровню –3 дБ, по ней оцените добротность контура Q = f_p / П. Запишите Q.

Установите в источнике Sine source частоту F = f_p. В режиме Transient Analysis постройте на одной системе координат графики напряжений на источнике v(V1), на конденсаторе v(C1) и на катушке v(L1). Обратите внимание на характер установления амплитуды колебаний и найдите время установления по уровню 0.9 от установившегося значения амплитуды. Проверьте, что оно может быть вычислено как 3*(2Q / 2pf_p), так как выражение в скобках имеет смысл постоянной времени контура. Обратите внимание на почти точное совпадение амплитуд напряжений на конденсаторе и катушке. Попытайтесь оценить разность между ними (конечно, с помощью одного или двух курсоров). Вычислите, во сколько раз эти напряжения больше по амплитуде напряжения на источнике. Эта величина должна быть равна добротности контура Q (поэтому и резонанс в последовательном контуре называют резонансом напряжений). Сравните ее с найденным по АЧХ значением добротности.

Установите в источнике Sine source частоту F = f_p+1 МГц. В режиме Transient Analysis постройте на одной системе координат те же графики напряжений на источнике v(V1), на конденсаторе v(C1) и на катушке v(L1). Амплитуда колебания теперь устанавливается по закону затухающей синусоиды. Найдите частоту этой синусоиды (подсказка: надо с помощью двух курсоров найти разность по времени между двумя соседними максимумами, т.е. период биений) и сравните её с разностью F - f_p. Обратите внимание на разницу между амплитудами v(C1) и v(L1).

Еще раз постройте АЧХ контура по рис. 2.1. Обратите внимание, что для частот, значительно больших и значительно меньших f_p, фильтр ведет себя как ФНЧ. Постройте с помощью режима Stepping семейство АЧХ для R1, изменяющегося от 3 до 33 Ом с шагом 5 Ом. Убедитесь, что при снижении добротности контур ведет себя как обычный нерезонансный ФНЧ.

Поменяйте местами L и C и опять постройте АЧХ (теперь выходным сигналом фильтра будет напряжение v(L1)). Обратите внимание на поведение АЧХ – теперь контур является фильтром ВЧ.

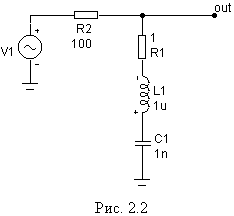
Включите последовательный колебательный контур с прежними значениями L и С как режекторный фильтр («фильтр-дырку») по рис. 2.2. Снимите АЧХ и ФЧХ фильтра v(out) и ph(v(out)). Обратите внимание, что теперь фильтр подавляет те частоты, которые подчеркивал фильтр по рис.2.1. Сделайте для себя вывод, что сопротивление последовательного контура на резонансной частоте имеет минимум.

2.2. Исследование параллельного колебательного контура.

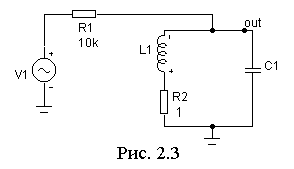Нарисуйте схему параллельного колебательного контура по рис. 2.3. Параметры источника Sine source пока не важны, С1 и L1 возьмите из пункта 2.1. Постройте в режиме AC Analysis АЧХ (и в децибелах, т.е. db(v(C1)), и в разах, т.е. v(С1)) и ФЧХ контура, т.е. ph(v(C1)) и по ним найдите точную резонансную частоту контура f_p. Запишите f_p. Найдите по графикам и запишите ширину полосы пропускания контура П по уровню –3 дБ, по ней оцените добротность контура Q = f_p / П. Запишите Q, сравните с добротностью последовательного контура, имеющего те же номиналы элементов.

Установите в источнике Sine source частоту F = f_p. В режиме Transient Analysis постройте на одной системе координат графики токов через источник i(V1), через конденсатор i(C1) и через катушку i(L1). Обратите внимание на характер установления амплитуды колебаний и найдите время установления по уровню 0.9 от установившегося значения амплитуды. Проверьте, что оно может быть вычислено как 3*(2Q / 2pf_p), так как выражение в скобках имеет смысл постоянной времени контура. Обратите внимание на почти точное совпадение амплитуд токов через конденсатор и катушку. Попытайтесь оценить разность между ними. Вычислите, во сколько раз эти токи больше по амплитуде тока через источник. Эта величина должна быть равна добротности контура Q (поэтому и резонанс в последовательном контуре называют резонансом токов). Сравните ее с найденным по АЧХ значением добротности.

Установите в источнике Sine source частоту F = f_p-0.5 МГц. В режиме Transient Analysis постройте на одной системе координат те же графики токов. Амплитуда колебания теперь устанавливается по закону затухающей синусоиды. Найдите частоту этой синусоиды (подсказка: надо с помощью двух курсоров найти разность по времени между двумя соседними максимумами, т.е. период биений) и сравните её с разностью f_p - F. Обратите внимание на увеличившуюся разницу между амплитудами i(C1) и i(L1).

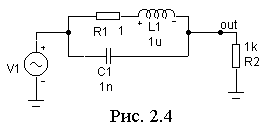
Включите параллельный колебательный контур с прежними значениями L и С как режекторный фильтр («фильтр-пробку») по рис. 2.4.

Снимите АЧХ и ФЧХ фильтра v(out) и ph(v(out)). Обратите внимание, что теперь фильтр подавляет те частоты, которые подчеркивал фильтр по рис.2.3. Сделайте для себя вывод, что сопротивление параллельного контура на резонансной частоте имеет максимум.

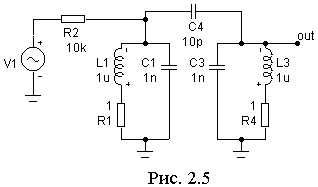Соберите двухконтурный полосовой фильтр на связанных одинаковых контурах по рис. 2.5. Емкости и индуктивности в контурах возьмите прежними. Снимите АЧХ и ФЧХ фильтра v(out) и ph(v(out)) для емкости связи С4 = 10р. Повторите моделирование, увеличивая С4 до 50р, 100р, 150р. (Удобно воспользоваться для этого режимом Stepping.) Обратите внимание, что на АЧХ при сильной связи между контурами появляется два максимума, хотя контура и одинаковы.

Далее необходимо добавить третий контур и снять АЧХ для такого многоконтурного фильтров. Добейтесь подбором частотозадающих элементов контуров АЧХ фильтра, близкой к прямоугольной.

Лабораторная работа №3