 |
Задачи для самостоятельного решения
|
|
|
|
Модуль № 2
Тема: Исследование концепции системы. Цепи Маркова.
Теоретические сведения
На первом этапе системного анализаанализируется состояние системы в реальных условиях, определяются несоответствия условий существования системы, выявляются причинно-следственные связи возникновения проблемных ситуаций, определяется степень актуальности проблемы в научном и практическом смысле.
Большое количество различных связей системы с внешней средой представим в виде одной входной и одной выходной связей, выделив их по принципу существенности в заданном отношении. По входным и выходным связям происходит обмен системы со средой путем передачи материальных, энергетических или информационных элементов.
Важной частью анализа проблемной ситуации является определение степени разрешимости проблемы. Необходимо хотя бы приблизительно оценить возможность решения проблемы.
Сложная система управления представляет собой объект дискретной природы, состоящий из большого числа элементов. В ходе исследования имеется возможность, воздействуя на вход системы анализировать ее реакцию на соответствующие входные воздействия.
Состояние системы в каждый момент времени может характеризоваться набором численных значений ее параметров. Эти параметры будем называть фазовыми координатами системы, а состояние системы изображать в виде точки S с этими координатами в некотором условном фазовом пространстве. Тогда изменение состояния системы в процессе ее эволюции соответствует некоторая траектория точки S в фазовом пространстве. Процесс эволюции системы во времени может протекать непрерывно или дискретно. Процесс в системе протекает дискретно, если состояние системы меняется лишь в определенные моменты времени, которые можно пронумеровать.
|
|
|
Описание поведения системы, процесс в которой протекает в дискретном фазовом пространстве, является достаточно сложным. Существует класс случайных процессов, для которых требуемое описание может быть получено более простым путем. Это класс Марковских случайных процессов.
Процесс, протекающий в физической системе, называется Марковским (или процессом без последствий), если для каждого момента времени поведение системы в будущем зависит только от состояния системы в данный момент и не зависит от того, каким образом система пришла в это состояние.
Случайный процесс с дискретным временем будет называться случайной последовательностью или случайной цепью.
Случайная цепь, для которой в каждый момент времени дальнейшая последовательность событий зависит только от состояния системы в данный момент, называется Марковской цепью.
Основной задачей исследования Марковской цепи является нахождение безусловных вероятностей нахождения системы S на любом
(k -м) шаге в состоянии 
обозначим эту вероятность 
( 1 )
где n – число дискретных состояний системы S.
Для нахождения вероятностей 
необходимо знать условные вероятности перехода системы S на k -м шаге в состояние 
если известно, что на предыдущем (k – 1)-м шаге она была в состоянии 
Обозначим эту вероятность:
( 2 )
Вероятности 
называются вероятностями перехода цепи Маркова на k -м шаге.
Вероятности перехода можно записать в виде матрицы перехода 
размерности 
( 3 )
Цепь Маркова называется однородной, если 
не зависят от номера шага 
Соотношение ( 7.3) примет вид:
( 4 )
Матрица безусловных вероятностей состояний на шаге k определяется соотношением:
( 5 )
Для 
справедливо соотношение:
( 6 )
Из ( 6 ) имеем:
( 7 )
Матрица финальных вероятностей Т вида:
|
|
|
( 8 )
может быть определена путем решения системы алгебраических уравнений:
( 9 )
Здесь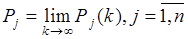 
– финальные вероятности.
Решение типовых задач
Пример 1. Система представляет собой техническое устройство, состоящего из m узлов (m = 3) и время от времени (в моменты 
подвергается профилактическому осмотру и ремонту. После каждого шага (момент осмотра и ремонта) система может оказаться в одном из следующих состоянии: 
– все узлы исправны; 
– один узел заменен новым, остальные исправны; 
– два узла заменены новыми, остальные исправны; 
– все три узла заменены новыми. Рассматривая состояния системы как марковскую цепь, вычислить вероятности состояний после трех шагов, т.е. 
В начальный момент времени все узлы исправны. Матрица перехода имеет вид:
Таким образом:
=?
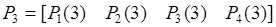Решение. Определим матрицу 
:
Так как в начальный момент времени система находится в состоянии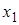 
, то:
Из (7) имеем:
;
.
;
Пример 2. Задана матрица перехода вида:
Найти матрицу финальных вероятностей Т вида:
Решение. Из ( 9 ) имеем для n = 3:
или
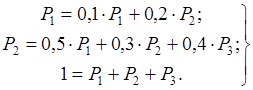( 10 )
Из ( 10 ) имеем:
( 11 )
Из ( 11 ) имеем:
или
( 12 )
Решим систему уравнений ( 12 ), используя правило Крамера. Имеем:
Таким образом:
Задачи для самостоятельного решения
Задача 1. Рассматривается следующий процесс: система представляет собой техническое устройство (ТУ), которая осматривается в определенные моменты времени (скажем, через сутки), и ее состояние регистрируется в отчетной ведомости. Каждый осмотр с регистрацией представляет собой “шаг” процесса. Возможные состояния ТУ следующие: – полностью исправно; – частично неисправно, требует наладки; – обнаружена серьезная неисправность, требует ремонта; – признано непригодным, списано. Матрица перехода:
В начальный момент (
) ТУ находится в состоянии (исправно). Найти распределение вероятностей состояний для первых трех шагов (
).
Задача 2. Задана матрица перехода вида:
Найти матрицу финальных вероятностей T вида:
Задача 3. В процессе эксплуатации ЭВМ может рассматриваться как физическая система, которая в результате проверки может оказаться в одном из следующих состояний: – ЭВМ полностью исправна; – ЭВМ имеет незначительные неисправности в ОП, но может решать задачи; – ЭВМ имеет существенные неисправности, может решать ограниченный класс задач; – ЭВМ полностью вышла из строя. В начальный момент ЭВМ полностью исправна. Проверка ЭВМ производится в фиксированные моменты времени 
Процесс, протекающий в системе, можно рассматривать как цепь Маркова с тремя шагами (1-я, 2-я, 3-я проверки ЭВМ). Матрица перехода:
|
|
|
Определить вероятности состояний после трех проверок, т.е.:
=?
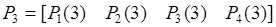Задача 4. Задана матрица перехода вида:
Найти матрицу финальных вероятностей T вида:
|
|
|
