 |
Чтение структурированных программ
|
|
|
|
Подпрограммы бывают двух видов: процедуры и функции. Процедуры просто выполняют последовательность операторов, а функции вычисляют значение и передают его в главную программу. Подпрограмма – процедура или подпрограмма – функция- это отдельный блок операторов, начинающийся с заголовка и заканчивающийся признаком конца процедуры или функции. Чтобы подпрограмма имела смысл ей надо получить какие-то значения, которые называются параметрами. Параметры, которые принимаются в подпрограмме, описываются в заголовке и называются формальными. Например,
Процедура Summa(a, b) – это заголовок подпрограммы - процедуры, имя которой Summa, а в скобках указываются формальные параметрыa и b.
Обращение из главной программы к процедуре осуществляется по имени подпрограммы-процедуры с перечнем в скобках параметров, которые ей передаются, например, Call Summa(x, y) – означает обратиться к процедуре Summa и передать ей параметры x и y, которые называются фактическими парамет рами.
Подпрограмма - функция оформляется таким образом:
Функция Длина(a, b, c, d), где Длина – имя функции, а в скобках указаны формальные параметры. Подпрограмма–функция возвращает только одно значение, которое обязательно присваивается названию функции в теле подпрограммы–функции. Так как функция возвращает значение, то обращение к ней из основной программы может входить в выражение, как операнд.
При выполнении процедуры или функции формальные параметры временно заменяются на фактические.
Задача 1. Составить на структурированном языке алгоритм вычисления периметра треугольника, если известны координаты его вершин (треугольник лежит на плоскости).
Обозначим координаты вершин xA, yA, xB, yB, xC, yC и ввод их значений осуществим в главной программе. Пусть AB-расстояние между точками A и B, BC-между B и C, AC-между A и С, а Р – периметр. Периметр вычислим по известной формуле Р=AB+BC+AC, а расстояние же между двумя точками вычислим по формуле: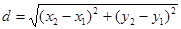 
. Вычисление расстояния между двумя точками вынесем в подпрограмму-функцию, назовем ее Длина, а формальные аргументы подпрограммы – функции обозначим через x1, y1, x2, y2. Тогда для вычисления AB, BC и AB надо три раза обратиться к подпрограмме-функции, передав ей значения фактических аргументов, сначала координаты, например, точек A и B, затем B и C, A и C.
|
|
|
Составим подпрограмму-функцию:
Функция Длина(x1, y1, x2, y2)
Длина=d
Конец функции
Основная программа:
Ввод координат вершин треугольника xA, yA, xB, yB, xC, yC.
P=Длина(xA,yA,xB,yB)+Длина(xB,yB,xC,yC)+Длина(xA,yA,xC,yC)
Вывод P
Задача 2. Дан массив целых чисел {Ai}, где i=1,2,3,…,M, причем М=15. Программа вычисляет произведение сумм некоторых элементов этого массива. Какое алгебраическое выражение описывает работу программы? В программе введены следующие константы: G=1; W=12; T=8; L=15.
Программа 15;
Начать функцию
Функция SUMMA(I1,I2);
S=0;
НЦ для I:=I1 до I2
S:=S+A(I)
КЦ;
SUMMA:=S
Конец функции;
Начать программу
Писать (‘Введите значение массива A’);
НЦ для J:=1 до M
Читать (A(J)
КЦ;
P:= SUMMA(G,W)*SUMMA(T,L);
Писать (‘Произведение равно:’, P:6);
Конец программы.
Варианты ответов:
1. 
2. 
3. 
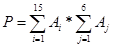4. 
Правильный ответ с номером 2.
4. Стратегии решения задач ( Этапы решения задач на ПК )
В процессе подготовки задачи (программной системы (ПС)) на ПК можно выделить такие этапы:
Постановка задачи
На этом этапе формулируется цель решения задачи, анализируются требования и подробно описывается содержание задачи, выявляются условия, при которых решается задача, а также определяются входные параметры, которые называются исходными данными. Например, для задачи 1, рассмотренной в предыдущей теме, целью является вычисление периметра треугольника, а исходными данными являются координаты его вершин, при этом условием является то, что вершины треугольника лежат на плоскости.
|
|
|
|
|
|
