Если да, докажите, если нет, приведите контрпример

Введение

Данное пособие предназначено для тех, кто хочет научиться решать задачи на доказательство по геометрии. Оно содержит пятьдесят задач, сформулированных в виде признаков равенства треугольников по трем элементам, включающим стороны, углы, высоты, медианы или биссектрисы треугольника. При этом используются обычные признаки равенства треугольников.

Особенностью предлагаемых задач является то, что это не просто задачи на доказательство. В них нужно самому выяснить, верно ли сформулированное утверждение. Если верно, то привести доказательство, если нет – дать контрпример.

Именно такие задачи характерны для исследовательской, творческой деятельности человека не только в математике, но и других различных областях знания. Не случайно, что многие научные проблемы формулируются в терминах задач с неопределенным условием.

Как правило, задачи с подобным неопределенным условием труднее, чем просто задачи на доказательство. Отсутствие уверенности в справедливости предложения, сформулированного в условии задачи, накладывает дополнительную психологическую трудность поиска решения. Но из этого не следует, что решением таких задач не следует заниматься на уроках математики. Наоборот, в них заложен большой образовательный и воспитательный потенциал. Они помогают более глубокому освоению изучаемого материала, учат отличать верное утверждение от неверного, развивают интуицию, логическое мышление, учат рассуждать, анализировать, аргументировать, доказывать.

Все включенные в пособие задачи сопровождаются рисунками, помогающими лучше понять условия задач, представить соответствующую геометрическую ситуацию, при необходимости провести дополнительные построения, наметить план решения.

В конце пособия даны решения всех задач.

В качестве дополнительной литературы рекомендуем следующую книгу:

Голубев В.И., Ерганжиева Л.Н., Мосевич К.К. Построение треугольника. – М.: БИНОМ, 2008.

В ней рассмотрены всевозможные построения треугольника по трем его элементам, включающим стороны, углы, биссектрисы, медианы, высоты, радиусы вписанной и описанной окружностей, периметр.

 

Выясните, верны ли следующие утверждения.

Если да, докажите, если нет, приведите контрпример

1. Два треугольника равны, если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника.

2. Два треугольника равны, если две стороны и высота, опущенная на одну из них, одного треугольника соответственно равны двум сторонам и высоте другого треугольника.

3. Два треугольника равны, если две стороны и высота, опущенная на третью сторону, одного треугольника соответственно равны двум сторонам и высоте другого треугольника.

4. Если угол, сторона, прилежащая к этому углу, и высота, опущенная на эту сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника, то эти треугольники равны.

5. Если угол, сторона, прилежащая к этому углу, и высота, опущенная на сторону, противоположную данному углу, одного треугольника соответственно равны углу, стороне и высоте другого треугольника, то эти треугольники равны.

6. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника, то эти треугольники равны.

7. Если угол, сторона, прилежащая к этому углу, и высота, опущенная на другую сторону, прилежащую к данному углу, одного треугольника соответственно равны углу, стороне и высоте другого треугольника, то эти треугольники равны.

8. Два треугольника равны, если два угла и высота, проведенная из вершины одного из них, соответственно равны двум углам и высоте другого треугольника.

9. Два треугольника равны, если два угла и высота, проведенная из вершины третьего угла, соответственно равны двум углам и высоте другого треугольника.

10. Если сторона и две высоты, опущенные на две другие стороны, одного треугольника соответственно равны стороне и двум высотам другого треугольника, то такие треугольники равны.

11. Если сторона и две высоты, одна из которых опущена на данную сторону, одного треугольника соответственно равны стороне и двум высотам другого треугольника, то такие треугольники равны.

12. Если угол и две высоты, опущенные на его стороны, одного треугольника соответственно равны углу и двум высотам другого треугольника, то такие треугольники равны.

13. Если угол и две высоты, одна из которых проведена из данного угла, одного треугольника, соответственно равны углу и двум высотам другого треугольника, то такие треугольники равны.

14. Если две стороны и медиана, проведенная к одной из них, одного треугольника соответственно равны двум сторонам и медиане другого треугольника, то такие треугольники равны.

15. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника, то такие треугольники равны.

16. Если угол, сторона, прилежащая к этому углу, и медиана, проведенная к этой стороне, одного треугольника соответственно равны углу, стороне и медиане другого треугольника, то эти треугольники равны.

17. Если угол, сторона, прилежащая к этому углу, и медиана, проведенная к стороне, противоположной данному углу, одного треугольника соответственно равны углу, стороне и медиане другого треугольника, то эти треугольники равны.

18. Если угол, сторона, противолежащая этому углу, и медиана, проведенная к другой стороне, одного треугольника соответственно равны углу, стороне и медиане другого треугольника, то эти треугольники равны.

19. Если угол, сторона, прилежащая к этому углу, и медиана, проведенная к другой стороне, прилежащей к данному углу, одного треугольника соответственно равны углу, стороне и медиане другого треугольника, то эти треугольники равны.

20. Два треугольника равны, если два угла и медиана, проведенная из вершины одного из них, соответственно равны двум углам и медиане другого треугольника.

21. Два треугольника равны, если два угла и медиана, проведенная из вершины третьего угла, соответственно равны двум углам и медиане другого треугольника.

22. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника, то такие треугольники равны.

23. Если сторона и две медианы, одна из которых проведена к данной стороне, одного треугольника соответственно равны стороне и двум медианам другого треугольника, то такие треугольники равны.

24. Если угол и две медианы, проведенные к его сторонам, одного треугольника соответственно равны углу и двум медианам другого треугольника, то такие треугольники равны.

25. Если угол и две медианы, одна из которых проведена из вершины данного угла, одного треугольника, соответственно равны углу и двум медианам другого треугольника, то такие треугольники равны.

26. Если две стороны и биссектриса, проведенная к одной из них, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника, то такие треугольники равны.

27. Ели две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника, то такие треугольники равны.

28. Если угол, сторона, прилежащая к этому углу, и биссектриса, проведенная к этой стороне, одного треугольника соответственно равны углу, стороне и биссектрисе другого треугольника, то эти треугольники равны.

29. Если угол, сторона, прилежащая к этому углу и биссектриса, проведенная из вершины этого угла, одного треугольника соответственно равны углу, стороне и биссектрисе другого треугольника, то эти треугольники равны.

30. Если угол, сторона, прилежащая к этому углу и биссектриса, проведенная к другой стороне, прилежащей к данному углу, одного треугольника соответственно равны углу, стороне и биссектрисе другого треугольника, то эти треугольники равны.

31. Два треугольника равны, если два угла и биссектриса, проведенная из вершины одного из них, соответственно равны двум углам и биссектрисе другого треугольника.

32. Два треугольника равны, если два угла и биссектриса, проведенная из вершины третьего угла, соответственно равны двум углам и биссектрисе другого треугольника.

33. Если у двух равнобедренных треугольников соответственно равны основания и опущенные на них высоты, то такие треугольники равны.

34. Если основание и высота, опущенная на боковую сторону, одного равнобедренного треугольника соответственно равны основанию и высоте другого равнобедренного треугольника, то такие треугольники равны.

35. Если основание и медиана, проведенная к боковой стороне, одного равнобедренного треугольника соответственно равны основанию и медиане другого равнобедренного треугольника, то такие треугольники равны.

36. Если основание и биссектриса, проведенная к боковой стороне, одного равнобедренного треугольника соответственно равны основанию и биссектрисе другого равнобедренного треугольника, то такие треугольники равны.

37. Два треугольника равны, если сторона, медиана и высота, проведенные к этой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

38. Два треугольника равны, если сторона, биссектриса и высота, проведенные к этой стороне, одного треугольника соответственно равны стороне, биссектрисе и высоте другого треугольника.

39. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

40. Два треугольника равны, если сторона, биссектриса и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, биссектрисе и высоте другого треугольника.

41. Два треугольника равны, если сторона, медиана и высота, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

42. Два треугольника равны, если сторона, биссектриса и высота, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне, биссектрисе и высоте другого треугольника.

43. Два треугольника равны, если угол, медиана и высота, проведенные из вершины этого угла, одного треугольника соответственно равны углу, медиане и высоте другого треугольника.

44. Два треугольника равны, если угол, биссектриса и высота, проведенные из вершины этого угла, одного треугольника соответственно равны углу, биссектрисе и высоте другого треугольника.

45. Два треугольника равны, если угол, медиана и высота, проведенные из вершин двух других углов, одного треугольника соответственно равны углу, медиане и высоте другого треугольника.

46. Два треугольника равны, если угол, медиана и высота, проведенные из вершины другого угла, одного треугольника соответственно равны углу, медиане и высоте другого треугольника.

47. Два треугольника равны, если угол, биссектриса и высота, проведенные из вершины другого угла, одного треугольника соответственно равны углу, биссектрисе и высоте другого треугольника.

48. Два треугольника равны, если угол, биссектриса, проведенная из его вершины, и высота, опущенная на сторону, прилежащую к этому углу, одного треугольника соответственно равны углу, биссектрисе и высоте другого треугольника.

49. Два треугольника равны, если три высоты одного треугольника соответственно равны трем высотам другого треугольника, то такие треугольники равны.

50. Два треугольника равны, если три медианы одного треугольника соответственно равны трем медианам другого треугольника, то такие треугольники равны.

Решения

1. Приведем пример, показывающий, что равенство указанных в задаче элементов треугольников ABC и A ₁ B ₁ C ₁ недостаточно для равенства самих треугольников.

Рассмотрим окружность и ее хорду AB. С центром в точке A проведем другую окружность, пересекающую первую окружность в некоторых точках C и C ₁. Тогда в треугольниках ABC и ABC ₁ AB – общая сторона, AC = A ₁ C ₁, С = С ₁, однако треугольники ABC и ABC ₁ не равны.

2. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, AC = A ₁ C ₁, высота CH равна высоте C ₁ H ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

 

 

Действительно, прямоугольные треугольники ACH и A ₁ C ₁ H ₁ равны по катету и гипотенузе. Значит, A = A ₁. Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, AС = A ₁ С ₁, A = A ₁. Следовательно, эти треугольники равны по двум сторонам и углу между ними.

3. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AC = A ₁ C ₁, BC = B ₁ C ₁, высота CH равна высоте C ₁ H ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

Действительно, прямоугольные треугольники ACH и A ₁ C ₁ H ₁ равны по катету и гипотенузе. Значит, ACH = A ₁ C ₁ H ₁. Аналогично, из равенства треугольников BCH и B ₁ C ₁ H ₁ следует, что BCH = B ₁ C ₁ H ₁. Таким образом, C = C ₁ и,следовательно, треугольники ABC и A ₁ B ₁ C ₁ равны по двум сторонам и углу между ними.

4. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, A = A ₁, высота CH равна высоте C ₁ H ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

Действительно, прямоугольные треугольники ACH и A ₁ C ₁ H ₁ равны по катету и острому углу. Значит, AC = A ₁ C ₁. Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, AС = A ₁ С ₁, A = A ₁. Следовательно, эти треугольники равны по двум сторонам и углу между ними.

5. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, A = A ₁, высота AH равна высоте A ₁ H ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

 

Действительно, прямоугольные треугольники ABH и A ₁ B ₁ H ₁ равны по катету и гипотенузе. Значит, B = B ₁. Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, A = A ₁, B = B ₁. Следовательно, эти треугольники равны по стороне и двум прилежащим к ней углам.

6. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, С = С ₁, высота AH равна высоте A ₁ H ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

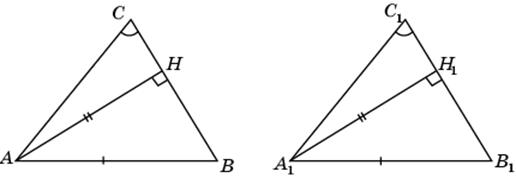Действительно, прямоугольные треугольники ABH и A ₁ B ₁ H ₁ равны по катету и гипотенузе. Значит, B = B ₁, откуда A = A ₁. Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, A = A ₁, B = B ₁. Следовательно, эти треугольники равны по стороне и двум прилежащим к ней углам.

7. Приведем пример, показывающий, что равенство указанных в задаче элементов треугольников ABC и A ₁ B ₁ C ₁ недостаточно для равенства самих треугольников.

Рассмотрим прямоугольные треугольники ABH и A ₁ B ₁ H ₁, в которых H = H ₁ = 90^o, AH = A ₁ H ₁, AB = A ₁ B ₁. На продолжениях сторон BH и B ₁ H ₁ отложим неравные отрезки соответственно HC и H ₁ C ₁. Тогда в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, B = B ₁, высоты AH и A ₁ H ₁ равны, однако сами треугольники не равны.

8. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ A = A ₁, B = B ₁, высота AH равна высоте A ₁ H ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

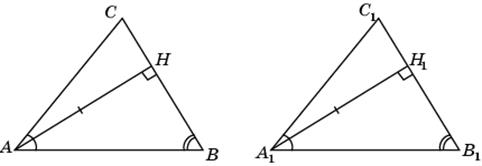Действительно, прямоугольные треугольники ABH и A ₁ B ₁ H ₁ равны по катету и острому углу. Значит, AB = A ₁ B ₁. Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, A = A ₁, B = B ₁. Следовательно, эти треугольники равны по стороне и двум прилежащим к ней углам.

9. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ A = A ₁, B = B ₁, высота CH равна высоте C ₁ H ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

Действительно, прямоугольные треугольники ACH и A ₁ C ₁ H ₁ равны по катету и острому углу. Значит, AC = A ₁ C ₁. Кроме того, из равенства углов A и A ₁, B и B ₁ следует равенство углов C и C ₁. Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AC = A ₁ C ₁, A = A ₁, C = C ₁. Следовательно, эти треугольники равны по стороне и двум прилежащим к ней углам.

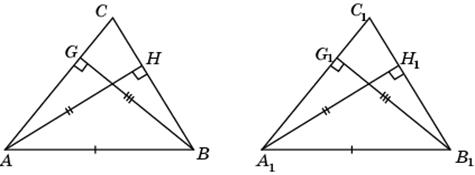10. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, высота AH равна высоте A ₁ H ₁, высота BG равна высоте B ₁ G ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

 

Действительно, прямоугольные треугольники ABG и A ₁ B ₁ G ₁ равны по катету и гипотенузе. Значит, A = A ₁. Аналогично, из равенства треугольников ABH и A ₁ B ₁ H ₁ следует, что B = B ₁. Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, A = A ₁, B = B ₁. Следовательно, эти треугольники равны по стороне и двум прилежащим к ней углам.

11. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, высота AH равна высоте A ₁ H ₁, высота CG равна высоте C ₁ G ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

 

 

Действительно, прямоугольные треугольники ABH и A ₁ B ₁ H ₁ равны по катету и гипотенузе. Значит, B = B ₁. Прямоугольные треугольники BCG и B ₁ C ₁ G ₁ равны по катету и острому углу. Значит, BC = B ₁ C ₁.Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, BC = B ₁ C ₁, B = B ₁. Следовательно, эти треугольники равны по двум сторонам и углу между ними.

12. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ A = A ₁, высота CH равна высоте C ₁ H ₁, высота BG равна высоте B ₁ G ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

 

Действительно, прямоугольные треугольники ABG и A ₁ B ₁ G ₁ равны по катету и острому углу. Значит, AB = A ₁ B ₁. Прямоугольные треугольники ACH и A ₁ C ₁ H ₁ равны по катету и острому углу. Значит, AC = A ₁ C ₁.Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, AC = A ₁ C ₁, A = A ₁. Следовательно, эти треугольники равны по двум сторонам и углу между ними.

13. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ C = C ₁, высота AG равна высоте A ₁ G ₁, высота CH равна высоте C ₁ H ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

Действительно, прямоугольные треугольники ACG и A ₁ C ₁ G ₁ равны по катету и острому углу. Значит, AC = A ₁ C ₁. Прямоугольные треугольники ACH и A ₁ C ₁ H ₁ равны по катету и гипотенузе. Значит, A = A ₁. Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AС = A ₁ С ₁, A = A ₁, C = C ₁. Следовательно, эти треугольники равны по стороне и двум прилежащим к ней углам.

14. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, AC = A ₁ C ₁, медиана СM равна медиане С ₁ M ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

Действительно, треугольники ACM и A ₁ C ₁ M ₁ равны по трем сторонам. Значит, A = A ₁. Таким образом, в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, AС = A ₁ С ₁, A = A ₁. Следовательно, эти треугольники равны по двум сторонам и углу между ними.

15. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AC = A ₁ C ₁, BC = B ₁ C ₁, медиана СM равна медиане С ₁ M ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

 

Продолжим медианы и отложим отрезки MD = CM и M ₁ D ₁ = C ₁ M ₁.

Тогда четырехугольники ACBD и A ₁ С ₁ B ₁ D ₁ – параллелограммы. Треугольники ACD и A ₁ C ₁ D ₁ равны по трем сторонам. Следовательно, ACD = A ₁ C ₁ D ₁. Аналогично, треугольники BCD и B ₁ C ₁ D ₁ равны по трем сторонам. Следовательно, BCD = B ₁ C ₁ D ₁. Значит, С = С ₁ и треугольники ABC и A ₁ B ₁ C ₁ равны по двум сторонам и углу между ними.

16. Приведем пример, показывающий, что равенство указанных в задаче элементов недостаточно для равенства самих треугольников.

 

Для этого рассмотрим окружность с центром в точке M. Проведем два диаметра AB и A ₁ B ₁. Через точки A, A ₁, M проведем еще одну окружность и выберем на ней точку C, как показано на рисунке. В треугольниках ABC и A ₁ B ₁ C AB = A ₁ B ₁, A = A ₁, медиана СM общая. Однако треугольники ABC и A ₁ B ₁ C не равны.

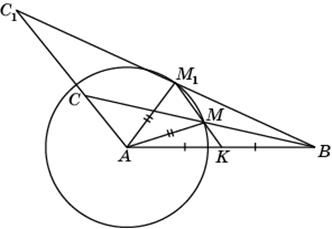
17. Приведем пример, показывающий, что равенство указанных в задаче элементов недостаточно для равенства самих треугольников. Для этого рассмотрим угол и окружность с центром в вершине A этого угла. На одной стороне угла отложим отрезок AB и через его середину K проведем прямую, параллельную другой стороне и пересекающую окружность в точках M и M ₁. Через точку B проведем прямые BM и BM ₁, пересекающие сторону угла соответственно в точках C и C ₁. В треугольниках ABC и ABC ₁ угол A общий, AB – общая сторона, медианы AM и AM ₁ равны, однако треугольники ABC и ABC ₁ не равны.

18. Приведем пример, показывающий, что равенство указанных в задаче элементов недостаточно для равенства самих треугольников. Для этого рассмотрим окружность с центром в точке O и окружность в два раза меньшего радиуса, касающуюся первой окружности внутренним образом в точке B. Напомним, что эта окружность без точки B является геометрическим местом середин хорд первой окружности, проходящих через точку B. Проведем хорду AB и окружность с центром в точке A, пересекающую вторую окружность в точках M и M ₁.Проведем прямые BM и BM ₁, пересекающие первую окружность соответственно в точках C и C ₁. В треугольниках ABC и ABC ₁ сторона AB общая, С = С ₁, медианы AM и AM ₁ равны. Однако треугольники ABC и ABC ₁ не равны.

 

19. Приведем пример, показывающий, что равенство указанных в задаче элементов недостаточно для равенства самих треугольников. Для этого рассмотрим окружность и проведем равные хорды AB и AB ₁. Через точку M окружности проведем прямые BM и B ₁ M и отложим на них отрезки MC и MC ₁ соответственно равные BM и B ₁ M. В треугольниках ABC и AB ₁ C ₁ AB = A ₁ B ₁, B = B ₁, медиана AM общая, однако треугольники ABC и AB ₁ C ₁ не равны.

20. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ A = A ₁, B = B ₁, медиана AM равна медиане A ₁ M ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

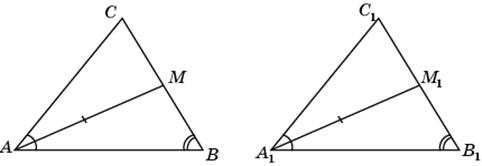Действительно, из равенства углов следует, что треугольники ABC и A ₁ B ₁ C ₁ подобны. Напомним, что преобразование подобия переводит медиану в медиану. Если бы AB A ₁ B ₁, то AM A ₁ M ₁, что противоречит условию.

Значит, AB = A ₁ B ₁ и, следовательно, треугольники ABC и A ₁ B ₁ C ₁ равны.

21. Решение аналогично решению предыдущей задачи.

22. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, медиана AM равна медиане A ₁ M ₁, медиана BK равна медиане B ₁ K ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

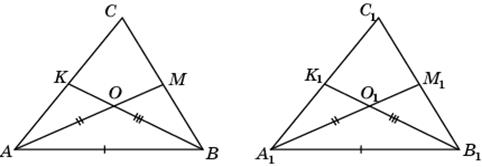Действительно, пусть O, O ₁ – точки пересечения медиан данных треугольников. Так как медианы в точке пересечения делятся в отношении 2:1, считая от вершины, то треугольники ABO и A ₁ B ₁ O ₁ равны по трем сторонам. Следовательно, BAO = B ₁ A ₁ O ₁ и, значит, треугольники ABM и A ₁ B ₁ M ₁ равны по двум сторонам и углу между ними. Поэтому ABC = A ₁ B ₁ C ₁. Аналогично доказывается, что BAC = B ₁ A ₁ C ₁. Таким образом, треугольники ABC и A ₁ B ₁ C ₁ равны по стороне и двум прилежащим к ней углам.

23. Пусть в треугольниках ABC и A ₁ B ₁ C ₁ AB = A ₁ B ₁, медиана AM равна медиане A ₁ M ₁, медиана СK равна медиане С ₁ K ₁. Докажем, что треугольники ABC и A ₁ B ₁ C ₁ равны.

Действительно, пусть O, O ₁ – точки пересечения медиан данных треугольников. Так как медианы в точке пересечения делятся в отношении 2:1, считая от вершины, то треугольники AKO и A ₁ K ₁ O ₁ равны по трем сторонам. Следовательно, KAO = K ₁ A ₁ O ₁ и, значит, треугольники ABM и A ₁ B ₁ M ₁ равны по двум сторонам и углу между ними. Поэтому ABC = A ₁ B ₁ C ₁ и MB = M ₁ B ₁ и, следовательно, BC = B ₁ C ₁. Таким образом, треугольники ABC и A ₁ B ₁ C ₁ равны по двум сторонам и углу между ними.

24. Приведем пример, показывающий, что равенство указанных в задаче элементов недостаточно для равенства самих треугольников. Для этого рассмотрим две равные окружности с центрами в точках O ₁ и O ₂,касающиеся друг друга в точке M. Проведем в одной из них хорду AB и прямую AM, пересекающую вторую окружность в некоторой точке C. Проведем отрезок BC. Получим треугольник ABC. Проведем в нем медиану CK и обозначим O точку, делящую еев отношении 2:1, считая от вершины C. Проведем окружность с центром в точке O радиуса OC, пересекающую вторую окружность в точке C ₁. Проведем прямую C ₁ M и обозначим A ₁ точку ее пересечения с первой окружностью. Обозначим K ₁ точку пересечения хорды A ₁ B и прямой C ₁ O. В треугол

Поделиться:

Воспользуйтесь поиском по сайту: